2023-2024年初中数学人教版七年级下学期期中模拟考试卷（二）（含答案）

这是一份2023-2024年初中数学人教版七年级下学期期中模拟考试卷（二）（含答案），共15页。试卷主要包含了单选题，填空题，解答题，实践探究题，综合题等内容，欢迎下载使用。

1．−4的倒数是（ ）
A．12B．−12C．−14D．−2
2．如图，AB∥CD，∠DFG=50°，EH是∠AEF的平分线，则∠HEF的度数是（ ）
A．50°B．55°C．60°D．65°
3．在平面直角坐标系中，点P(−5，6)位于（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
4．下列命题是假命题的是（ ）
A．若a<0，则1+a<1−a
B．若a=0，b=0，则ab=0
C．三角形的重心是这个三角形的三条角平分线的交点
D．等腰三角形顶角的平分线、底边上的中线、底边上的高相互重合
5．如图，在正方形网格中，每个小正方形的顶点称为格点.点M，N均在格点上，以某一个格点为原点，适当方向为x，y轴的正方向，取相同单位长度建立平面直角坐标系，则下列是同一个坐标系中点M，N的坐标的是（ ）
A．M(−2，0)，N(1，1)B．M(−1，0)，N(0，2)
C．M(−4，−4)，N(2，−2)D．M(1，2)，N(5，3)
6．如图，下列能判定AB∥CD的条件有几个（ ）
（1）∠1=∠2 （2）∠3=∠4（3）∠B=∠5 （4）∠B+∠BCD=180°.
A．4B．3C．2D．1
7．如图，AB//CD，EC平分∠AEF，若∠EFD=130°，则∠ECF的度数是（ ）
A．50°B．55°C．60°D．65°
8．如图所示，已知数轴上的点A、O、B、C、D分别表示数﹣2、0、1、2、3，则表示数3 −5 的点P应落在（ ）
A．线段AO上B．线段OB上C．线段BC上D．线段CD上
9．估计(7+7)×77的值应在（ ）
A．3和4之间B．4和5 之间C．5和6之间D．6和7之间
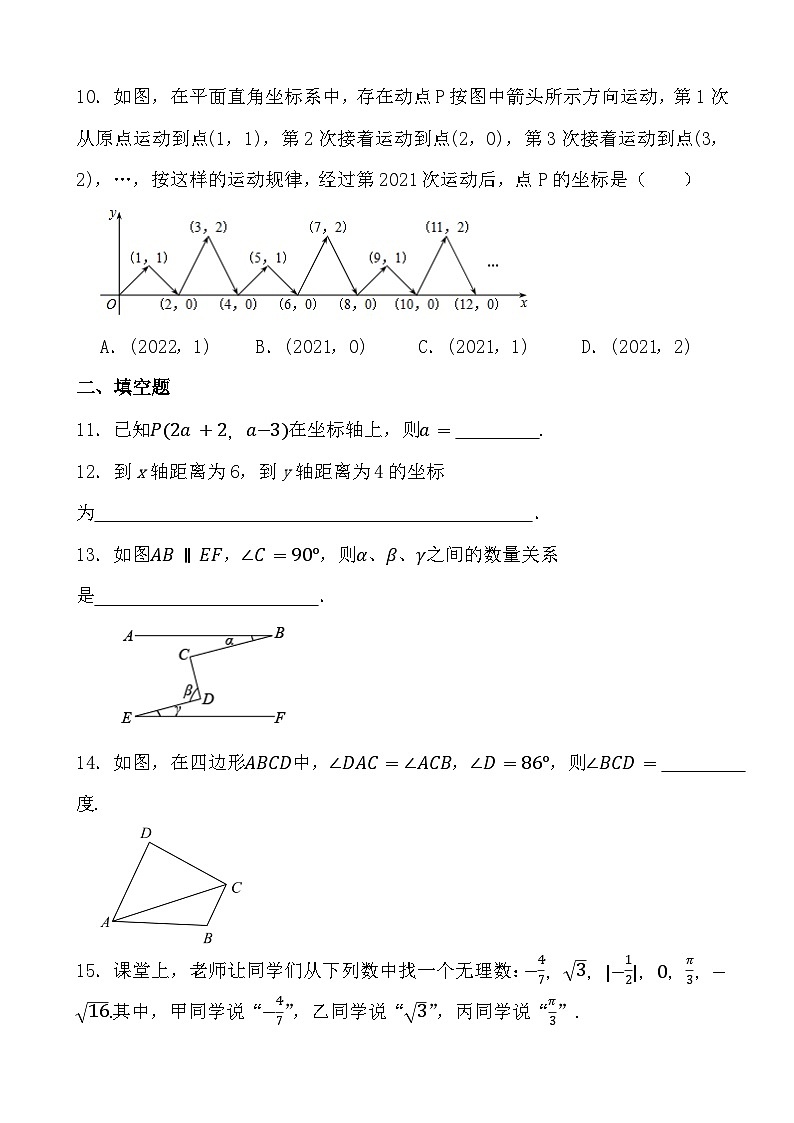
10．如图，在平面直角坐标系中，存在动点P按图中箭头所示方向运动，第1次从原点运动到点(1，1)，第2次接着运动到点(2，0)，第3次接着运动到点(3，2)，…，按这样的运动规律，经过第2021次运动后，点P的坐标是（ ）
A．(2022，1)B．(2021，0)C．(2021，1)D．(2021，2)
二、填空题
11．已知P(2a+2，a−3)在坐标轴上，则a= .
12．到x轴距离为6，到y轴距离为4的坐标为 ．
13．如图AB∥EF，∠C=90°，则α、β、γ之间的数量关系是 ．
14．如图，在四边形ABCD中，∠DAC=∠ACB，∠D=86°，则∠BCD= 度.
15．课堂上，老师让同学们从下列数中找一个无理数：−47，3，|−12|，0，π3，−16.其中，甲同学说“−47”，乙同学说“3”，丙同学说“π3”.
（1）甲、乙、丙三位同学中，说错的是 .
（2）请将老师所给的数字按要求填入横线内：
整数： ；
负分数： .
16．如图，已知AB∥CD，E、F分别在AB、CD上，点G在AB、CD之间，连接GE、GF，∠BEG=40°，EP平分∠BEG，FP平分∠DFG，在CD的下方有一点Q，EG平分∠BEQ，FD平分∠GFQ，求∠Q+2∠P的度数为 ．
三、解答题
17．已知，如图，∠1＝∠ACB，∠2＝∠3，FH⊥AB于H．试说明：CD⊥AB．
18．如图，直线AB，CD相交于点O，已知∠BOC=75°、ON将∠AOD成两个角，且∠AON：∠NOD=2：3．求∠AON的度数．
19．如图1，直线MN与直线AB，CD分别交于点E，F，∠BEM与∠DFN互为补角
（1）请判断直线AB与CD的位置关系，并说明理由；
（2）如图2，∠BEF与∠EFD的角平分线EP与FP交于点P，延长EP与CD交于点G，过点G作GH⊥EG垂足为G，求证：PF∥HG；
（3）在（2）的条件下，连接PH，点K是GH上一点，连接PK，使∠PHK=∠HPK，作∠EPK的平分线PQ交MN于点Q，请画出图形．并直接写出∠HPQ的度数．
四、实践探究题
20．下面是小李同学探索107的近似数的过程：
∵面积为107的正方形边长是107，且10＜107＜11，
∴设107＝10+x，其中0＜x＜1， 画出如图示意图，
∵图中S正方形＝102+2×10•x+x2，S正方形＝107
∴102+2×10•x+x2＝107
当x2较小时，省略x2，得20x+100≈107，得到x≈0.35，即107≈10.35．
（1）76的整数部分是 ；
（2）仿照上述方法，探究76的近似值．（画出示意图，标明数据，并写出求解过程）
21．操作探究：已知在纸面上有一数轴(如图所示)．
（1）折叠纸面，使表示1与-1的点重合，则表示-2的点与表示 的点重合．
（2）折叠纸面，使表示-1的点与表示3的点重合，回答以下问题．
①表示5的点与表示数 的点重合．
②表示3的点与表示数 的点重合．
③若数轴上A，B两点之间的距离为9(A在B的左侧)，且A，B两点经折叠后重合，此时点A表示的数是 ，点B表示的数是
（3）已知在数轴上点A表示的数是a，将点A移动4个单位长度，此时点A表示的数和a互为相反数，求a的值．
五、综合题
22．如图1，直线AB∥CD，△ABE的顶点E在AB与CD之间.
（1）若∠ABE=150°，∠BAE=20°.
①当∠CDE=2∠EDM时，求∠BED的度数.
②如图2，作出∠CDE的角平分线DF，当DF平行于△ABE中的一边时，求∠BED的度数.
（2）如图3，∠CDE的角平分线DF交EB的延长线于点H，连结BF，当∠ABH=2∠HBF，12∠BED+13∠F=40°时，求∠CDE的度数.
23．如图，已知射线CB∥DA，∠C=∠DAB=120°，E，F在射线CB上，且满足DB平分∠ADF，DE平分∠CDF．
（1）求证：CD∥BA；
（2）求∠DEC−∠BDA的度数．
24．已知：如图，DB平分∠ADC，∠1+∠2＝180°．
（1）求证：AB∥CD；
（2）若ED⊥DB，∠A=50°，求∠EDC的大小．
答案解析部分
1．【答案】B
2．【答案】D
3．【答案】B
4．【答案】C
5．【答案】A
6．【答案】（1）B
7．【答案】D
8．【答案】B
9．【答案】A
10．【答案】C
11．【答案】3或-1
12．【答案】（4，6），（-4，6），（-4，-6）或（4，-6）
13．【答案】∠α+∠β−∠γ=90°
14．【答案】94
15．【答案】（1）甲
（2）0， −16；−47
16．【答案】120°
17．【答案】解： CD⊥AB；
理由：∵∠1=∠ACB，
∴ED∥CB．
∴∠2=∠BCD．
∵∠2=∠3，
∴∠3=∠BCD，
∴FH∥CD，
∵FH⊥AB，
∴CD⊥AB．
18．【答案】解：由∠AON：∠NOD=2：3，可设∠AON=2x，∠NOD=3x，
∴∠AOD=5x，
∵∠BOC=75°，
∴∠AOD=5x=75°，
∴x=15°，
∴∠AON=30°．
19．【答案】（1）解：AB//CD，理由如下：
∵∠BEM+∠DFN=180°，∠BEM+∠BEF=180°，∠DFN+∠DFE=180°，
∴∠BEF+∠DFE=180°，
∴AB//CD（同旁内角互补，两直线平行）．
（2）解：由（1）得，AB//CD，
∴∠BEF+∠EFD=180°，
∵∠BEF与∠EFD的角平分线交于点P，
∴∠FEP+∠EFP=12（∠BEF+∠EFD）=90°，
∴∠EPF=90°，
又∵GH⊥EG，
∴∠HGE=90°，
∴∠EPF=∠HGE，
∴PF//GH．
（3）解：如图所示：
∵∠PHK=∠HPK，
∴∠PKG=2∠HPK，
又∵∠KPG=90°-∠PKG=90°-2∠HPK，
∴∠EPK=180°-∠KPG=90°+2∠HPK，
∵PQ平分∠EPK，
∴∠QPK=12∠EPK=45°+∠HPK，
∴∠HPQ=∠QPK−∠HPK=45°．
20．【答案】（1）8
（2）解：∵面积为76的正方形边长是76，且8＜76，
∴设76＝8+x，如图所示，
∵图中S正方形＝82+2×8•x+x2，S正方形＝76，
∴82+2×8•x+x2＝76，
当x2较小时，省略x2，得16x+64≈76，得到x≈0.75，
即76≈8.75．
21．【答案】（1）2
（2）-3；2-3；-3.5；5.5
（3）解：∵ 在数轴上点A表示的数是a，将点A移动4个单位长度 ，
∴点A所表示的数为a-4或a+4，
∵平移后点A所表示的数与a互为相反数，
∴a-4+a=0或a+4+a=0，
解得a=2或-2，
∴a的值为2或-2.
22．【答案】（1）解：①如图，过点E在作EG∥CD，
∵AB∥CD，
∴AB∥CD∥EG，
∴∠NBE=∠BEG，∠GED=∠EDM，
∵∠NBE+∠ABE=180°，∠ABE=150°，
∴∠NBE=∠BEG=180°−∠ABE=30°；
∵∠CDE+∠EDM=180°，∠CDE=2∠EDM，
∴∠EDM=∠GED=60°，
∴∠BED=∠NBE+∠EDM=∠GED+∠BEG=90°；
②分两种情况：
（i）当DF∥BE时，设DF与AB交于点P，如图所示，
∵∠NBE+∠ABE=180°，∠ABE=150°，
∴∠NBE=180°−∠ABE=30°；
∵DF∥BE，
∴∠NBE=∠BPD=30°，
∵AB∥CD，
∴∠CDP=∠BPD=30°，
∵DF平分∠CDE，
∴∠CDE=2∠CDP=60°，
∴∠EDM=180°−∠CDE=120°，
∴由①得∠BED=∠NBE+∠EDM=30°+120°=150°；
（ii）当DF∥AE时，设DF与AB交于点P，如图所示，∠BAE=20°，
∴∠BAE=∠BPD=20°，
∵AB∥CD，
∴∠CDP=∠BPD=20°，
∵DF平分∠CDE，
∴∠CDE=2∠CDP=40°，
∴∠EDM=180°−∠CDE=140°，
∵∠NBE+∠ABE=180°，∠ABE=150°，
∴∠NBE=180°−∠ABE=30°；
∴由①得∠BED=∠NBE+∠EDM=30°+140°=170°；
（2）解：设DF与AB交于点P，如图所示，
设∠ABH=2∠HBF=2x，∠CDF=∠EDF=y，则∠CDE=2∠CDF=2y，
∵AB∥CD，
∴∠BPD=∠CDF=y，
∴在△BPF中，
∠BPD=∠F+∠ABF=∠F+∠ABH+∠HBF=∠F+3x，
即y=3x+∠F，
由（1）小题可得∠BED=∠NBE+∠EDM=∠ABH+180°−∠CDE=2x+180°−2y，
∵12∠BED+13∠F=40°，
∴90°+x−y+13y−x=40°.
∴y=75°，
∴∠CDE=2∠CDF=2y=150°.
23．【答案】（1）证明：∵CB∥DA，∠C=∠DAB=120°，
∴∠CDA=180°−∠C=180°−120°=60°，
∴∠CDA+∠DAB=180°，
∴CD∥BA
（2）解：∵CB∥DA，
∴∠DEC=∠EDA，∠C+∠CDA=180°
∴∠CDA=180°−∠C=60°
∵DB平分∠ADF，DE平分∠CDF
∴∠FDB=12∠FDA，∠EDF=12∠CDF，
∴∠EDB=∠FDB+∠EDF=12∠FDA+12∠CDF=12∠CDA=12×60°=30°；
∴∠DEC－∠BDA=∠EDA−∠BDA=∠EDB=30
24．【答案】（1）证明：∵∠1+∠2=180°，∠1+∠DCB=180°，
∴∠2=∠DCB，
∴AB∥CD；
（2）解：∵AB∥CD，
∴∠ABD=∠BDC，
∵DB平分∠ADC，
∴∠ADB=∠BDC，
∴∠ABD=∠ADB，
∵∠A=50°，
∴∠ABD=∠ADB=（180°-50°）÷2=65°，
∵ED⊥DB，
∴∠EDB=90°，
∴∠EDC=∠EDB-∠BDC=90°-65°=25°．