人教A版 学业考试复习 必修一 第三章 第一课时　函数的概念与性质 课件

这是一份人教A版 学业考试复习 必修一 第三章 第一课时　函数的概念与性质 课件，共60页。PPT课件主要包含了考点一，函数及其表示，知识梳理，函数的概念，深化认知，答案42，｜方法总结｜，考点二，函数的单调性与最值，函数的单调性等内容，欢迎下载使用。
第1课时　函数的概念与性质
The part ne
考向（一）　函数的概念及其表示
2. 函数的表示法表示函数的常用方法有解析法、图象法和列表法.
3. 分段函数（1）若函数在其定义域的不同子集上，因对应关系不同而分别用几 个不同的式子来表示，这种函数称为分段函数.（2）分段函数的定义域等于各段函数的定义域的并集，其值域等于 各段函数的值域的并集，分段函数虽由几个部分组成，但它表 示的是一个函数.
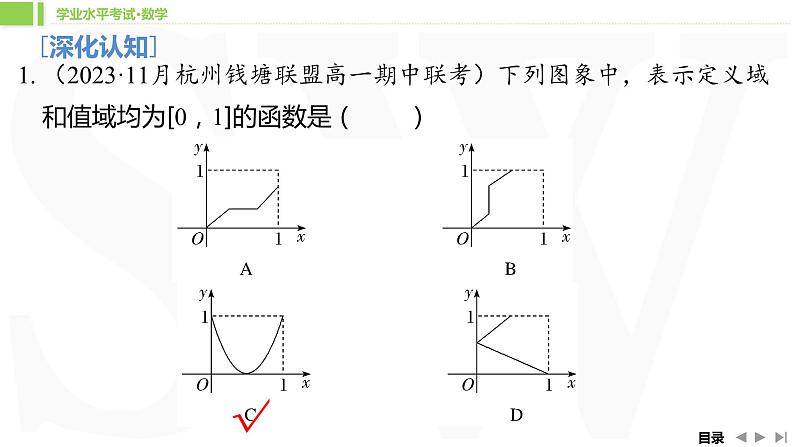
1. （2023·11月杭州钱塘联盟高一期中联考）下列图象中，表示定义域 和值域均为[0，1]的函数是（　　）
解析：　对于A，定义域为[0，1]，但是值域不是[0，1]，故 A错误；对于B，定义域不是[0，1]，值域为[0，1]，故B错误；对于C，定义域和值域均为[0，1]，故C正确；对于D，不满足函数的定义，故D错误.故选C.
2. （多选）（2023·11月浙东北联盟高一期中联考） 已知函数 f （ x ） 是一次函数，满足 f （ f （ x ））＝4 x ＋9，则 f （ x ）的解析式可能 为（　　）
解析： f （－1）＝－1＋5＝4； f [ f （－1）]＝ f （4）＝lg24＝2.
｜方法总结｜分段函数的求解策略（1）根据分段函数解析式求函数值首先确定自变量的值属于哪个区间，其次选定相应的解析式 代入求解.（2）已知函数值或函数值范围求自变量的值或范围应根据每一段的解析式分别求解，但要注意检验所求自变量 的值或范围是否符合相应段的自变量的取值范围.
考向（二）　函数的定义域与值域 [知识梳理]1. 在函数 y ＝ f （ x ）， x ∈ A 中， x 叫做自变量， x 的取值范围 A 叫做 函数的定义域；与 x 的值相对应的 y 值叫做函数值，函数值的集合{ f （ x ）｜ x ∈ A }叫做函数的值域.2. 如果两个函数的定义域相同，并且对应关系完全一致，则这两个函 数为同一个函数.
（1）满足不等式 a ≤ x ≤ b 的实数 x 的集合叫做闭区间，表示为[ a ，b ]；（2）满足不等式 a ＜ x ＜ b 的实数 x 的集合叫做开区间，表示为 （ a ， b ）；（3）满足不等式 a ＜ x ≤ b 或 a ≤ x ＜ b 的实数 x 的集合叫做半闭半开 区间，分别表示为（ a ， b ]或[ a ， b ），定义域和值域经常用 区间表示. 这里的实数 a 与 b 都叫做相应区间的端点.
3. 设 a ， b 是两个实数，而且 a ＜ b ，我们规定
5. （2020·7月浙江学考）函数 f （ x ）＝2 x 的值域是（　　）
解析：　函数 f （ x ）＝2 x 的值域是（0，＋∞）.故选B.
1. 函数的定义域是指使得函数有意义的自变量的取值集合，因此可以 根据如何使函数有意义来建立不等式或不等式组，通过解不等式 （组）来求得函数的定义域，求解过程中要注意函数在实际背景下 定义域的可能限制.2. 对于一个函数来说，当其对应关系与定义域确定时，其函数的值域 也随之确定.因此函数的值域要根据函数的定义域与对应关系来处理. 常见的求函数值域的方法有观察法、配方法、换元法等，有时也可 以根据函数的图象直接得到函数的值域.
考向（三）　函数的图象 [知识梳理]1. 利用描点法作函数的图象（1）确定函数的定义域；（2）化简函数的解析式；（3）讨论函数的性质（如奇偶性、单调性、周期性）；（4）画出函数图象.
① y ＝ f （ x ）的图象向左平移 h （ h ＞0） 个单位长度，得到 y ＝ f （ x ＋ h ）的图象.② y ＝ f （ x ）的图象向右平移 h （ h ＞0） 个单位长度，得到 y ＝ f （ x － h ）的图象.③ y ＝ f （ x ）的图象向上平移 k （ k ＞0） 个单位长度，得到 y ＝ f （ x ）＋ k 的图象.④ y ＝ f （ x ）的图象向下平移 k （ k ＞0） 个单位长度，得到 y ＝ f （ x ）－ k 的图象.
2. 利用图象变换法作函数的图（1）平移变换
（3）对称变换① y ＝ f （ x ）与 y ＝ f （－ x ）的图象关于 y 轴对称.② y ＝ f （ x ）与 y ＝－ f （ x ）的图象关于 x 轴对称.③ y ＝ f （ x ）与 y ＝－ f （－ x ）的图象关于原点对称.④ y ＝ ax （ a ＞0且 a ≠1）与 y ＝lg ax （ a ＞0且 a ≠1）的图象关于 y ＝ x 对称.
（4）翻折变换① y ＝｜ f （ x ）｜的图象是将 y ＝ f （ x ）的图象在 x 轴下方的 图象向上翻折，其余部分不变而得到的.② y ＝ f （｜ x ｜）的图象是通过先作出 y ＝ f （ x ）当 x ≥0的图 象，再关于 y 轴对称作 y ＝ f （ x ）当 x ＜0的图象而得到的.
8. 把函数 y ＝（ x －2）2＋2的图象向左平移1个单位长度，再向上平移 1个单位长度，所得图象对应的函数解析式是（　　）
解析：　把函数 y ＝（ x －2）2＋2的图象向左平移1个单位长度 后得到 y ＝[（ x ＋1）－2]2＋2＝（ x －1）2＋2的图象，再将 y ＝（ x －1）2＋2的图象向上平移1个单位长度后得到 y ＝（ x － 1）2＋3的图象.
A. y ＝（ x －3）2＋3B. y ＝（ x －3）2＋1C. y ＝（ x －1）2＋3D. y ＝（ x －1）2＋1
9. 函数 y ＝｜lg（ x －1）｜的图象是（　　）
解析：　将函数 y ＝lg x 的图象先向右平移1个单位长度，可得到函 数 y ＝lg（ x －1）的图象，再将所得函数图象位于 x 轴下方的图象关 于 x 轴翻折，位于 x 轴上方的图象不变，可得到函数 y ＝｜lg（ x － 1）｜的图象.故符合条件的图象为选项C中的图象.
The part tw
（2）单调区间的定义 如果函数 y ＝ f （ x ）在区间 I 上单调递增或单调递减，那么就 说函数 y ＝ f （ x ）在这一区间具有（严格的）单调性，区间 I 叫做 y ＝ f （ x ）的单调区间.
10. （2022·1月浙江学考）已知函数 f （ x ）＝ x 2－2 ax ＋ b 在区间（－ ∞，1]上单调递减，则实数 a 的取值范围是（　　）
解析：　函数 f （ x ）＝ x 2－2 ax ＋ b 图象的对称轴为 x ＝ a ，且开 口向上，函数 f （ x ）在区间（－∞，1]上单调递减，所以 a ∈[1， ＋∞）.故选A.
11. 下列函数中，在区间[1，＋∞）上单调递增的是（　　）
12. （2023·11月台州山海协作体高一期中联考）已知函数 f （ x ）＝ x 2－ 2 tx ＋1在区间[2，5]上单调且有最大值8，则实数 t 的值为 　　　　.
｜方法总结｜熟练掌握函数的单调性的定义以及常见函数的单调性的判断方 法，能够判断给出函数的单调性及其单调区间.
The part three

考向（一）　函数的奇偶性
2. 函数奇偶性的三个重要结论（1）如果一个奇函数 f （ x ）在原点处有定义，即 f （0）有意义， 那么一定有 f （0）＝0；（2）如果函数 f （ x ）是偶函数，那么 f （ x ）＝ f （｜ x ｜）；（3）奇函数在两个关于原点对称的区间上具有相同的单调性；偶函 数在两个关于原点对称的区间上具有相反的单调性.
13. （2020·7月浙江学考）已知 f （ x ）是奇函数，其部分图象如图所示，则 f （ x ）的图象是（　　）
解析：　因为奇函数的图象关于原点对称，所以B符合题意.故 选B.
14. （2021·7月浙江学考）已知函数 f （ x ）＝2｜ x ｜＋ ax 2， a ∈R，则 f （ x ）的图象不可能是（　　）
解析：　函数 f （ x ）＝2｜ x ｜＋ ax 2的定义域为R. 因为 f （－ x ） ＝2｜－ x ｜＋ a （－ x ）2＝2｜ x ｜＋ ax 2＝ f （ x ），所以函数 y ＝ f （ x ）为偶函数.，其图象关于 y 轴对称，对照四个选项的图象，只 有D不符合.故选D.
15. （2022·1月浙江学考）已知函数 y ＝2 ax 3（ a ＞0），则此函数 是（　　）
解析：　令 y ＝ f （ x ）＝2 ax 3，则函数 y ＝ f （ x ）＝2 ax 3的定义 域为R，且 f （－ x ）＝2 a （－ x ）3＝－2 ax 3＝－ f （ x ），所以函 数 y ＝ f （ x ）＝2 ax 3是奇函数，又因为 a ＞0，所以函数 y ＝ f （ x ） ＝2 ax 3在（－∞，＋∞）上单调递增.故选D.
考向（二）　函数的周期性 [知识梳理]1. 周期函数：对于函数 y ＝ f （ x ），如果存在一个非零常数 T ，使得 当 x 取定义域内的任何值时，都有 f （ x ＋ T ）＝ f （ x ），那么就称 函数 y ＝ f （ x ）为周期函数，称 T 为这个函数的周期.2. 最小正周期：如果在周期函数 f （ x ）的所有周期中存在一个最小的 正数，那么这个最小正数就叫做 f （ x ）的最小正周期.
3. 函数周期性的三个常用结论
16. 已知函数 f （ x ）是定义在R上的奇函数，且满足 f （ x ＋2）＝－ f （ x ），则 f （2 022）＝（　　）
解析：　因为 f （ x ＋2）＝－ f （ x ），所以 f （ x ＋4）＝－ f （ x ＋2）＝ f （ x ），即函数 f （ x ）是周期为4的周期函数.又因为函数 f （ x ）是定义在R上的奇函数，所以 f （0）＝0，所以 f （2）＝－ f （0）＝0， f （2 022）＝ f （505×4＋2）＝ f （2）＝0.故选B.
17. （2023·7月浙江学考）已知 f （ x ）是定义域为R的偶函数，且 f （ x ）＋ f （2－ x ）＝4，则 f （2 023）＝ 　　　　.
The part fur
5. 函数 f （ x ）的部分图象如图所示，则 f （ x ）的解析式可能 是（　　）
6. （2023·11月浙南名校联盟高一期中联考）已知函数 y ＝ f （ x ）的定 义域是R，值域为[－2，1]，则下列函数的值域也为[－2，1]的 是（　　）
7. 若函数 f （ x ）＝ x 2＋2（ a －1） x ＋2在区间（－∞，4] 上单调递 减，则实数 a 的取值范围是（　　）
8. （2023·11月浙南名校联盟高一期中联考）已知函数 f （ x ）是定义在 实数集R上的偶函数，则下列结论一定成立的是（　　）
解析：　∵函数 f （ x ）是定义在实数集R上的偶函数，∴ f （－ x ）＝ f （ x ），故A、B错误；∀ x ∈R， f （ x ） f （－ x ）≥0，故C正确，D错误.
9. （2023·11月浙南名校联盟高一期中联考）已知函数 f （ x ）的定义域 为R，函数 g （ x ）＝ f （ x ）＋ x 2为奇函数，且 g （ x －4）＝ g （ x ），则 f （－6）的值为（　　）
解析：　因为函数 g （ x ）＝ f （ x ）＋ x 2为奇函数，所以有 g （－2）＝－ g （2），又 g （ x －4）＝ g （ x ），所以 g （－2）＝ g （2），得 g （－2）＝ g （2）＝0，则 g （－6）＝ g （－2）＝0. 即 g （－6）＝ f （－6）＋（－6）2＝0，所以 f （－6）＝－36.故选B.
11. （2023·11月嘉兴八校联盟高一期中联考）已知 f （ x ）是定义在R 上的偶函数，且函数 f （ x ＋1）的图象关于原点对称，若 f （0）＝ 1，则 f （－1）＋ f （2）的值为（　　）
解析：　因为 f （ x ）是定义在R上的偶函数，所以 f （－ x ）＝ f （ x ）.又因为函数 f （ x ＋1）的图象关于原点对称，所以函数 f （ x ）的图象关于（1，0）对称，即－ f （ x ）＝ f （2－ x ）.令 x ＝1，则－ f （1）＝ f （1），即 f （－1）＝ f （1）＝0，令 x ＝2，则 f （2）＝－ f （0）＝－1，所以 f （－1）＋ f （2）＝0－1＝－1.故选B.
二、多项选择题13. （2023·11月嘉兴八校联盟高一期中联考）下面各组函数中是同一 函数的是（　　）
14. （2023·11月嘉兴八校联盟高一期中联考）下列函数中，既是偶函 数又在区间（0，＋∞）上单调递增的是（　　）
T 为非零有理数，若 x 是有理数，则 x ＋ T 是有理数，所以满足 f （ x ＋ T ）＝ f （ x ）＝1；若 x 是无理数，则 x ＋ T 也是无理数，所以满 足 f （ x ＋ T ）＝ f （ x ）＝0，即任意一个非零有理数 T ， f （ x ＋ T ）＝ f （ x ）对任意 x ∈R恒成立，故D正确.故选B、C、D.
解析：因为1＞0，所以 f （1）＝lg21＝0，又因为－2＜0，所以 f （－2）＝－（－2）＝2，所以 f （ f （－2））＝ f （2）＝lg22＝1.
答案：{ x ｜ x ≤2且 x ≠1}
解析：①当 a ＜0时，函数 f （ x ）在（－∞， a ）上单调递减，因 此 f （ x ）不存在最大值；
③当0＜ a ≤3时，函数 f （ x ）在（ a ，3）上单调递增，在（3，＋ ∞）上单调递减，故 x ≥ a 时， f （ x ）＝8－（ x －3）2≤8，当 x ＜ a 时，函数 f （ x ）在（－∞， a ）上单调递增，此时 f （ x ） ＜ f （ a ）＝ a 2－9 ，于是 a 2－9≤8时，函数 f （ x ）存在最大值.又0＜ a ≤3，解得0＜ a ≤3；④当 a ＞3时，函数 f （ x ）在（ a ，＋∞）上单调递减， f （ x ）≤ f （ a ）＝8－（ a －3）2 ，在（－∞， a ）上单调递增，此时 f （ x ）＜ f （ a ）＝ a 2－9.故当8－（ a －3）2≥ a 2－9时，函数 f （ x ）存在最大值，解得－1≤ a ≤4，又 a ＞3，故3＜ a ≤4.综上， a 的取值范围是0≤ a ≤4.
（2）判断 f （ x ）在[0，＋∞）上的单调性，并利用单调性的定义证明；
（3）若 f （2 a ＋1）＋ f （2－ a 2）＞0，求实数 a 的取值范围.
解：（3） f （ x ）在[0，＋∞）上单调递增，且函数 f （ x ）为R上 的奇函数，故 f （ x ）为R上的增函数.由 f （2 a ＋1）＋ f （2－ a 2）＞0，得 f （2 a ＋1）＞－ f （2－ a 2）＝ f （ a 2－2），于是2 a ＋1＞ a 2－2 ，所以 a 2－2 a －3＝（ a －3）（ a ＋1）＜0，解得－1＜ a ＜3，即实数 a 的取值范围为（－1，3）.
解：（1）因为函数 f （ x ）是奇函数且定义域为R，所以满足 f （－ x ）＝－ f （ x ）且 f （0）＝0.则当 x ＝0时， f （0）＝－ a ＝0，解得 a ＝0.