人教A版 学业考试复习 必修一 第二章 第二课时　二次函数与一元二次方程、不等式 课件

这是一份人教A版 学业考试复习 必修一 第二章 第二课时　二次函数与一元二次方程、不等式 课件，共60页。PPT课件主要包含了考点一，知识梳理，深化认知，考点二，绝对值不等式，课时跟踪检测，答案－33等内容，欢迎下载使用。

The part ne
一元二次不等式及其解法

2. 从函数的观点看一元二次不等式（1）一元二次不等式的解法
①一元二次不等式经过变形，可以化为两种标准形式： ax 2＋ bx ＋ c ＞0或 ax 2＋ bx ＋ c ＜0（其中 a ＞0）；②计算相应的判别式Δ；③当Δ≥0时，求出相应的一元二次方程的根；④利用二次函数的图象与 x 轴的相关位置确定一元二次不等式 的解集.
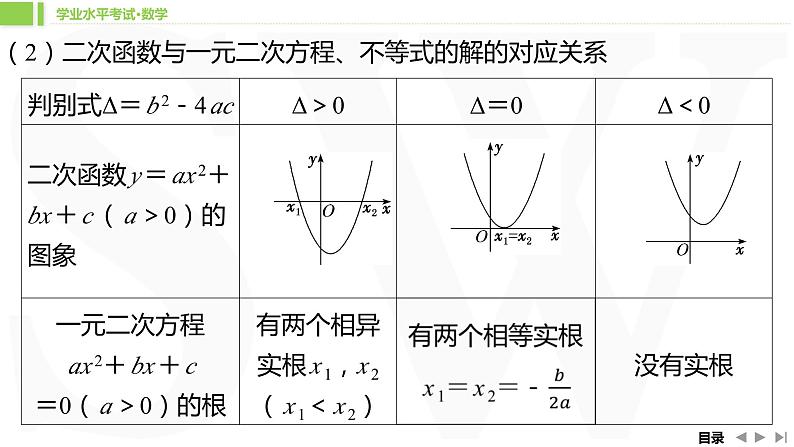
（2）二次函数与一元二次方程、不等式的解的对应关系
1. （2022·1月浙江学考）不等式 x 2－4 x ＜0的解集是（　　）　　　　　　 　　　　　 　　　　　
解析：　 x 2－4 x ＜0⇒ x （ x －4）＜0，解得0＜ x ＜4，所以不等式 的解集为（0，4）.故选A.
｜方法总结｜求解一元二次不等式，可以利用因式分解法，通过因式的正负 构造不等式组，进而通过解不等式组求得解集；也可以利用函数与 方程思想，结合该不等式相应的二次函数的图象与零点，求得不等 式的解集.
2. （2023·11月浙东北联盟高一期中联考）已知 x 2－ bx ＋ c ＜0的解集 为（－1， t ）（ t ＞－1），则 b ＋ c 的值为（　　）
3. 当 x ∈R时，不等式 x 2－2 x －1－ a ≥0恒成立，则实数 a 的取值范围 是（　　）
解析：　由题意知，当 x ∈R时，不等式 x 2－2 x －1－ a ≥0恒 成立，故Δ＝（－2）2＋4（1＋ a ）≤0，
解得 a ≤－2，故实数 a 的取值范围是（－∞，－2].故选A.
The part tw
　　[知识梳理]1. 绝对值不等式的解法
（1）含绝对值的不等式｜ x ｜＜ a 与｜ x ｜＞ a 的解集
（2）｜ ax ＋ b ｜≤ c （ c ＞0）和｜ ax ＋ b ｜≥ c （ c ＞0）型不等式的解法①｜ ax ＋ b ｜≤ c ⇔－ c ≤ ax ＋ b ≤ c ；②｜ ax ＋ b ｜≥ c ⇔ ax ＋ b ≥ c 或 ax ＋ b ≤－ c .
（3）｜ x － a ｜＋｜ x － b ｜≥ c （ c ＞0）和｜ x － a ｜＋｜ x － b ｜ ≤ c （ c ＞0）型不等式的解法①利用绝对值不等式的几何意义求解，体现了数形结合的思想；②利用“零点分段法”求解，体现了分类讨论的思想；③通过构造函数，利用函数的图象求解，体现了函数与方程的思想.
2. 绝对值不等式的性质（1）如果 a ， b 是实数，则｜ a ＋ b ｜≤｜ a ｜＋｜ b ｜，当且仅当 ab ≥0时，等号成立；（2）｜｜ a ｜－｜ b ｜｜≤｜ a ± b ｜≤｜ a ｜＋｜ b ｜；（3）如果 a ， b ， c 是实数，那么｜ a － c ｜≤｜ a － b ｜＋｜ b － c ｜，当且仅当（ a － b ）（ b － c ）≥0时，等号成立.
4. （2020·1月浙江学考）不等式｜ x －1｜＜2的解集是（　　）　
解析：　由｜ x －1｜＜2得－2＜ x －1＜2，解得－1＜ x ＜3.故选A.
5. 关于 x 的不等式｜ x ｜＋｜ x －1｜≥3的解集是（　　）
解析：　当 x ≥1时，原不等式化为 x ＋ x －1≥3，解得 x ≥2；当0 ＜ x ＜1时，原不等式化为 x － x ＋1≥3，无解；当 x ≤0时，原不等 式化为－ x － x ＋1≥3，解得 x ≤－1.综上可知，原不等式的解集为 （－∞，－1]∪[2，＋∞）.故选C.
（2）若 f （ x ）在[－1，1]上有零点，求证：当 a ≥－1时， c ≤｜ b ｜＋｜ a －1｜.
The part three
4. （2023·杭州钱塘联盟高一期中联考） 若集合 A ＝{ x ｜1＜ x ＜2}， B＝{ x ｜ x 2－4 x ＋3≥0}，则 A ∪（∁R B ）＝（　　）
解析：　∵ B ＝{ x ｜ x 2－4 x ＋3≥0}＝{ x ｜ x ≤1或 x ≥3}，∴∁R B ＝{ x ｜1＜ x ＜3}，则 A ∪（∁R B ）＝{ x ｜1＜ x ＜3}.故选B.
5. 不等式｜2 x ＋1｜－｜ x －1｜＞0的解集是（　　）
7. （2023·11月台州一中高一期中）设 x ∈R，则“ x 2－2 x ＜0”是“｜ x －1｜＜2”的（　　）
解析：　由 x 2－2 x ＜0得 x ∈（0，2），由｜ x －1｜＜2得 x ∈（－ 1，3），故“ x 2－2 x ＜0”是“｜ x －1｜＜2”的充分不必要条件.故选A.
10. 若不等式－ x 2－2 x ＋ a ＋2≤0对任意的 x ∈（1，3）恒成立，则实 数 a 的取值范围是（　　）
解析：　不等式－ x 2－2 x ＋ a ＋2≤0对任意的 x ∈（1，3）恒成 立，转化为不等式 x 2＋2 x － a －2≥0对任意的 x ∈（1，3） 恒成 立，记 f （ x ）＝ x 2＋2 x － a －2，其图象开口向上，对称轴为 x ＝ －1，当 x ∈（1，3）时，该函数单调递增，要想 f （ x ）≥0在 x ∈ （1，3）时恒成立，只需 f （1）≥0⇒3－ a －2≥0⇒ a ≤1.故选B.
11. 已知方程 x 2－4 x ＋ a ＝0的两实数根都大于1，则实数 a 的取值范围 是（　　）
12. （2023·杭州四校高一联考） 命题 p ：∃ x ∈{ x ｜1≤ x ≤9}， x 2－ ax ＋36≤0，若 p 是真命题，则实数 a 的取值范围为（　　）
二、多项选择题13. 下列不等式的解集为R的是（　　）
14. （2023·杭州四校高一联考）若不等式 ax 2－ bx ＋ c ＞0的解集是 （－1，2），则下列选项正确的是（　　）
15. 已知关于 x 的不等式 a （ x －1）（ x ＋3）＋2＞0的解集是（ x 1， x2），其中 x 1＜ x 2，则下列结论中正确的是（　　）
如图所示，由图知 x 1＜－3＜1＜ x 2，｜ x 1－ x2｜＞4，故B错误，C正确.故选A、C、D.
16. （2023·杭州四校高一联考） 已知函数 y ＝ x 2＋ ax ＋ b （ a ＞0）有 且只有一个零点，则（　　）
解得 c ＝4，故D正确.故选A、B、D.
三、填空题17. 已知 二 次 函 数 y ＝ ax 2＋ bx ＋ c （ a ≠0）的图象如图所示，那么 二次函数 y ＝ ax 2＋ bx ＋ c （ a ≠0）的零点是 　　　　；一元二次 不等式 ax 2＋ bx ＋ c ≥0的解集是 　　　　.
答案：－1，2　{ x ｜ x ≤－1或 x ≥2}
解析：根据图象可得函数 y ＝ ax 2＋ bx ＋ c （ a ≠0）的零点是 －1，2.一元二次方程 ax 2＋ bx ＋ c ＝0（ a ≠0）的实数根分别是－1， 2，则一元二次不等式 ax 2＋ bx ＋ c ≥0（ a ≠0）的解集是{ x ｜ x ≤－1或 x ≥2}.
18. 关于 x 的不等式 x 2－2｜ x ｜－3＜0的解集是 　　　　　　.
解析：当 x ≥0时，不等式化为 x 2－2 x －3＜0，
解得－1＜ x ＜3，即0≤ x ＜3；当 x ＜0时，不等式化为 x 2＋2 x －3＜0，
解得－3＜ x ＜1，即－3＜ x ＜0.综上所述，不等式的解集为（－3，3）.
答案：（－∞，－1）∪[0，＋∞）
20. （2023·11月杭州钱塘联盟高一期中联考） 已知关于 x 的不等式 ax 2 ＋ bx ＋ c ＞0的解集为（－∞，－3）∪（6，＋∞），则不等式 cx 2 ＋ bx ＋ a ＞0的解集为 　　　　.
四、解答题21. （2023·11月浙东北联盟高一期中联考）设集合 A ＝{ x ∈R｜｜ x － 1｜≤1}， B ＝{ x ∈R｜1－ m ≤ x ≤ m ＋6}.（1）若 B ＝⌀，求实数 m 的取值范围；
（2）若 A ∩ B ＝ A ，求实数 m 的取值范围.
（1）当 m ＝1时，求 A ∩（∁R B ）；
（2）若 A ∪ B ＝ A ，求实数 m 的取值范围.
23. （2023·杭州四校高一联考）已知二次函数 y ＝ ax 2＋ bx ＋2（ a ， b 为实数）.（1）当 x ＝1时， y ＝1，且对∀ x ∈（2，5）， y ＞0恒成立，求实 数 a 的取值范围；
令 t ＝ x －2，则 t ∈（0，3），
（2）当 x ＝1时， y ＝1，且对∀ a ∈[－2，－1]， y ＞0恒成立，求 实数 x 的取值范围；