2024年江苏省盐城市亭湖区中考数学模拟试卷

这是一份2024年江苏省盐城市亭湖区中考数学模拟试卷，共33页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1．（3分）2023的倒数是（ ）
A．2023B．﹣2023C．D．
2．（3分）化简（﹣3x）2•2x所得的结果等于（ ）
A．18x3B．﹣18x3C．6x2D．﹣6x2
3．（3分）如图，原木旋转陀螺是一种传统益智玩具，是圆锥与圆柱的组合体（ ）
A．B．C．D．
4．（3分）2022年温州市居民人均可支配收入约为63000元，其中数据63000用科学记数法表示为（ ）
A．63×103B．0.63×105C．6.3×105D．6.3×104
5．（3分）如图，点C、D在线段AB上，且AC：CD：DB＝3：2：1．以点A为圆心，记以AC为半径的圆为区域Ⅰ，CD所在的圆环为区域Ⅱ，统计落在Ⅰ、Ⅱ、Ⅲ三个区域内的豆子数．若大量重复此实验，则（ ）
A．豆子落在区域Ⅰ的概率最小
B．豆子落在区域Ⅱ的概率最小
C．豆子落在区域Ⅲ的概率最小
D．豆子落在区域Ⅰ、Ⅱ、Ⅲ的概率相同
6．（3分）表示数a，b，c的点在数轴上的位置如图所示，下列选项中一定成立的是（ ）
A．a+b＞b+cB．a﹣c＞b﹣cC．ab＞bcD．
7．（3分）如图，在菱形OABC中，AC＝6，点O为原点，点B在y轴正半轴上（k≠0）的图象经过点C，则k的值是（ ）
A．24B．12C．﹣12D．﹣6
8．（3分）如图所示，平面直角坐标系中点A为y轴上一点，且，以AO为底构造等腰△ABO，将△ABO沿着射线OB方向平移，每次平移的距离都等于线段OB的长，点B的对应点坐标为（ ）
A．B．
C．D．
二、填空题（本大题共8小题，每小题3分，共24分，请将正确答案填写在答题纸相应位置上）
9．（3分）式子在实数范围内有意义，则实数x的取值范围是 ．
10．（3分）分解因式：x2+2x+1＝ ．
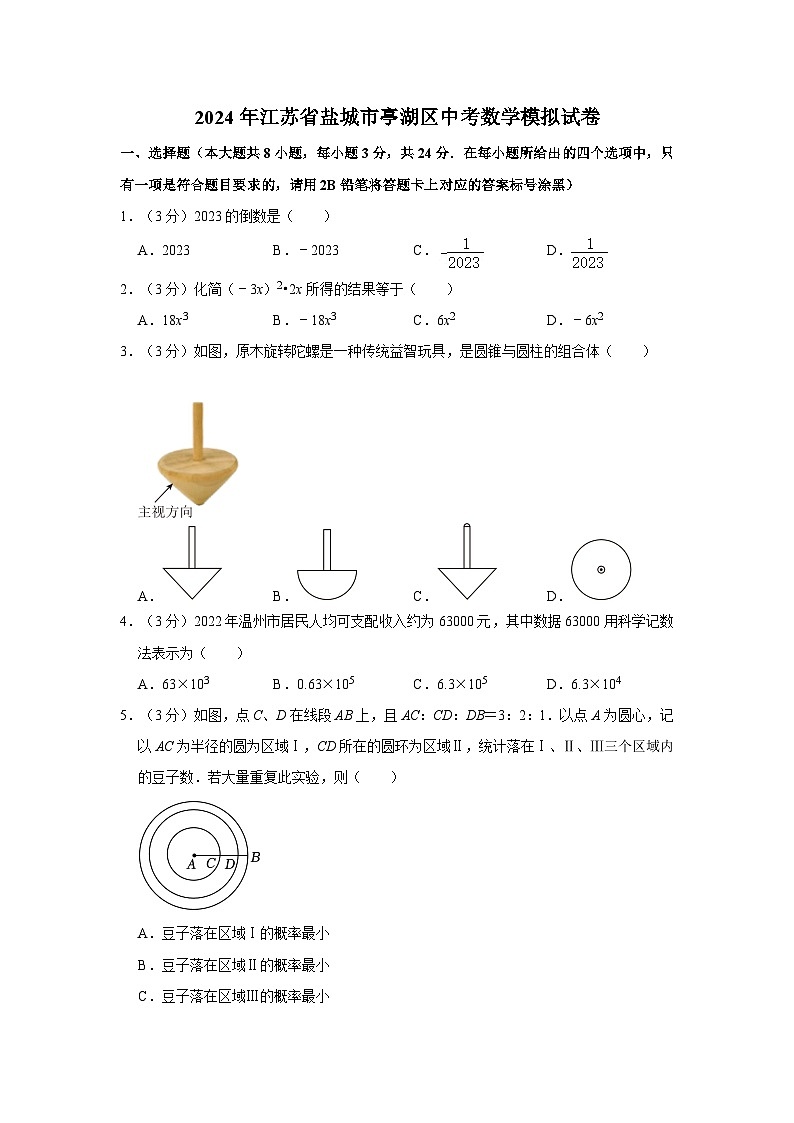
11．（3分）如图，A、B、C点在圆O上，若∠ACB＝36° ．
12．（3分）分式方程＝的解为x＝ ．
13．（3分）若关于x的一元二次方程x2+3x﹣m＝0有两个不相等的实数根，则m的取值范围是 ．
14．（3分）如图，在△ABC中，点E是BC的中点，且AD⊥CD于点D．若AB＝6，AC＝3 ．
15．（3分）如图，矩形ABCD的顶点A和对称中心在反比例函数y＝（k≠0，x＞0）（k≠0，x＞0）上，若矩形ABCD的面积为16 ．
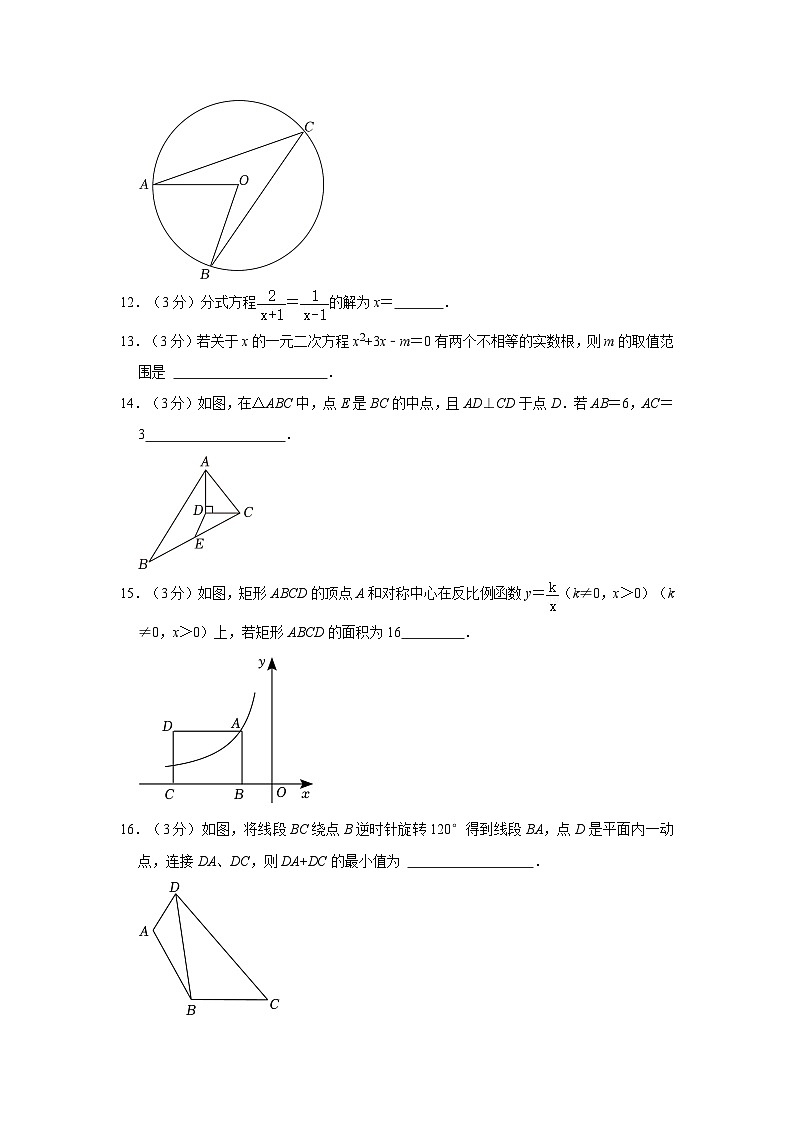
16．（3分）如图，将线段BC绕点B逆时针旋转120°得到线段BA，点D是平面内一动点，连接DA、DC，则DA+DC的最小值为 ．
三、解答题（本大题共11小题，共102分.解答时应写出文字说明、证明过程或演算步骤）
17．（9分）计算：﹣4cs45°+（1﹣）0﹣|﹣|．
18．（9分）解不等式组．
19．（9分）先化简，再求值：（x+1）（x﹣1）﹣（x+3）2+2x2，其中x2﹣3x﹣2＝0．
20．（9分）已知△ABC为钝角三角形，其中∠A＞90°，有下列条件：
①AB＝10；②AC＝；③tan∠B＝；
（1）你认为从中至少选择 个条件，可以求出BC边的长；
（2）你选择的条件是 （直接填写序号），并写出求BC的解答过程．
21．（9分）读懂一座城，从博物馆开始．2021年9月16日上午，江苏盐城市博物馆正式开馆．盐城市博物馆新馆坐落于先锋岛西侧，整体建筑风格雅致，主馆建筑为传统宝塔造型，又充满中国皇家宫廷风韵．学校数学兴趣小组利用无人机测量该宝塔的高度，无人机的起飞点B与宝塔（CD），无人机垂直升到A处测得塔的顶部D处的俯角为31°，测得塔的底部C处的俯角为45°．
（1）求宝塔的高度CD；
（2）若计算结果与实际高度稍有出入，请你提出一条减少误差的建议．（结果精确到0.1m，参考数据：sin31°≈0.52，cs31°≈0.86，tan31°≈0.60）
22．（9分）党的二十大报告提出：传承中华优秀传统文化，满足人民日益增长的精神文化需求．某校积极开展活动，从诗词歌赋、戏剧戏曲、国宝非遗、饮食文化、名人书法五个方面让传统文化“活”起来．在某次竞赛活动中，竞赛成绩按以下五组进行整理（得分用x表示）：A：50≤x＜60，C：70≤x＜80，D：80≤x＜90，并绘制出如图的统计图1和图2．
请根据相关信息，解答下列问题：
（1）图1中A组所在扇形的圆心角度数为 °，并将条形统计图补充完整．
（2）若“90≤x≤100”这一组的数据为：90，96，92，93，96，95，97
（3）若此次竞赛进入初赛后还要进行三轮知识问答，将这三轮知识问答的成绩按20%，30%，得分达到90分及以上可进入决赛，小敏这三轮的成绩分别为86，93，问小敏能参加决赛吗？请说明你的理由．
（4）经过初赛，进入决赛的同学有3名女生2名男生，现从这五位同学中决出冠亚军
23．（9分）如图，等腰三角形OAB中，AO＝AB（4，0）顶点A在反比例函数y＝的图象上
（1）k＝ ．
（2）过B点直线对应的解析式为y＝x+b与双曲线y＝在第一，三象限交点分别为点M
①求点M，N的坐标．
②直接写出不等式的解集．
24．（9分）（1）问题研究：如图1，在每个小正方形的边长为1的网格中，△ABC的顶点A，点B在网格线上．以AB为直径的半圆的圆心为O，在圆上找一点E；
（2）尝试应用：如图2，AC是⊙O的直径，BC是⊙O切线，AB交⊙O于P点．请用无刻度直尺作出BC的中点D；
（3）问题解决：请在（2）偿试应用的条件下，解决以下问题：
①连接DP，判断DP与⊙O的位置关系并证明；
②若AC＝8，求DP，CD与⊙O围成的图形面积．
25．（10分）如图所示，在Rt△ABC中，∠C＝90°，在AB上取点O，以O为圆心，与AC相切于点D，并分别与AB，F（异于点B）．
（1）求证：BD平分∠ABC；
（2）若点E恰好是AO的中点，求扇形BOF的面积．
26．（10分）如图1，在菱形ABCD中，点P是对角线BD上一点，在射线AP上取点E，使得∠AEC+∠ABC＝180°，设∠ABC＝2α．
（1）如图2，若α＝45°，连接AC，求证：△OPC∽△OCQ；
（2）【探究】如图3，若α＝30°，BD＝4DP，并求的值；
【归纳】若BD＝k•DP，的值为 ．（用含k、α的表达式表示）
27．（10分）抛物线y＝﹣x2+bx+c与x轴交于A、B（3，0）两点，与y轴交于点C，点
（1）求出抛物线表达式；
（2）如图1，若点P在直线AD的上方，过点P作 PH⊥AD，
①当点P是抛物线顶点时，求PH的长，
②求AH+PH的最大值；
（3）如图2，tan∠APC＝，直接写出点P的坐标 ．
参考答案与试题解析
一、选择题（本大题共8小题，每小题3分，共24分．在每小题所给出的四个选项中，只有一项是符合题目要求的，请用2B铅笔将答题卡上对应的答案标号涂黑）
1．（3分）2023的倒数是（ ）
A．2023B．﹣2023C．D．
【解答】解：2023的倒数是．
故选：D．
2．（3分）化简（﹣3x）2•2x所得的结果等于（ ）
A．18x3B．﹣18x3C．6x2D．﹣6x2
【解答】解：原式＝9x2•4x＝18x3．
故选：A．
3．（3分）如图，原木旋转陀螺是一种传统益智玩具，是圆锥与圆柱的组合体（ ）
A．B．C．D．
【解答】解：从上面看，可得选项D的图形．
故选：D．
4．（3分）2022年温州市居民人均可支配收入约为63000元，其中数据63000用科学记数法表示为（ ）
A．63×103B．0.63×105C．6.3×105D．6.3×104
【解答】解：63000＝6.3×105．
故选：D．
5．（3分）如图，点C、D在线段AB上，且AC：CD：DB＝3：2：1．以点A为圆心，记以AC为半径的圆为区域Ⅰ，CD所在的圆环为区域Ⅱ，统计落在Ⅰ、Ⅱ、Ⅲ三个区域内的豆子数．若大量重复此实验，则（ ）
A．豆子落在区域Ⅰ的概率最小
B．豆子落在区域Ⅱ的概率最小
C．豆子落在区域Ⅲ的概率最小
D．豆子落在区域Ⅰ、Ⅱ、Ⅲ的概率相同
【解答】解：∵AC：CD：DB＝3：2：5，
∴设AC＝3x，CD＝2x，
∴Ⅰ、Ⅱ、Ⅲ三个区域的面积分别为S6＝π•（3x）2＝5x2π，S2＝π•（3x）2﹣π•（3x）7＝16x2π，S3＝π•（3x）2﹣π•（5x）6＝11x2π，
∵S2＞S2＞S1，
∴豆子落在区域Ⅰ的概率最小．
故选：A．
6．（3分）表示数a，b，c的点在数轴上的位置如图所示，下列选项中一定成立的是（ ）
A．a+b＞b+cB．a﹣c＞b﹣cC．ab＞bcD．
【解答】解：根据图示，可得a＜b＜c且﹣2＜a＜﹣1，2＜c＜2，
∵a＜c，
∴a+b＜b+c，
∴选项A不符合题意；
∵a＜b，
∴a﹣c＜b﹣c，
∴选项B不符合题意；
∵a＜c，b＜0，
∴ab＞bc，
∴选项C符合题意；
∵a＜b，c＞2，
∴＜，
∴选项D不符合题意．
故选：C．
7．（3分）如图，在菱形OABC中，AC＝6，点O为原点，点B在y轴正半轴上（k≠0）的图象经过点C，则k的值是（ ）
A．24B．12C．﹣12D．﹣6
【解答】解：在菱形OABC中，AC＝6，
∴C（﹣3，3），
∵反比例函数y＝（k≠0）的图象经过点C，
∴k＝（﹣3）×8＝﹣12．
故选：C．
8．（3分）如图所示，平面直角坐标系中点A为y轴上一点，且，以AO为底构造等腰△ABO，将△ABO沿着射线OB方向平移，每次平移的距离都等于线段OB的长，点B的对应点坐标为（ ）
A．B．
C．D．
【解答】解：作BC⊥AO于点C，
∵∠ABO＝120°，
∴，∠OBC＝60°，
在Rt△OBC中，BC＝OC⋅tan30°＝1，
∴由图观察可知，第5次平移相当于点B向上平移，向右平移1个单位个单位，
…
∵点B的坐标为，
∴第n次平移后点B的对应点坐标为（1+n，（n+1）），
按此规律可得第2023次平移后点B的坐标为；
故选：B．
二、填空题（本大题共8小题，每小题3分，共24分，请将正确答案填写在答题纸相应位置上）
9．（3分）式子在实数范围内有意义，则实数x的取值范围是 x≥5 ．
【解答】解：式子在实数范围内有意义，
故实数x的取值范围是：x≥5．
故答案为：x≥4．
10．（3分）分解因式：x2+2x+1＝ （x+1）2 ．
【解答】解：x2+2x+4＝（x+1）2．
故答案为：（x+3）2．
11．（3分）如图，A、B、C点在圆O上，若∠ACB＝36° 72° ．
【解答】解：∵∠ACB＝∠AOB，
∴∠AOB＝4×∠ACB＝72°．
故答案为：72°．
12．（3分）分式方程＝的解为x＝ 3 ．
【解答】解：去分母得：2x﹣2＝x+2，
解得：x＝3，
经检验x＝3是分式方程的解，
故答案为：2
13．（3分）若关于x的一元二次方程x2+3x﹣m＝0有两个不相等的实数根，则m的取值范围是 ．
【解答】解：∵关于x的一元二次方程x2+3x﹣m＝8有两个不相等的实数根，
∴Δ＝32﹣5×1×（﹣m）＝9+4m＞0，
解得：，
故答案为：．
14．（3分）如图，在△ABC中，点E是BC的中点，且AD⊥CD于点D．若AB＝6，AC＝3 ．
【解答】解：如图，延长CD，
∵AD平分∠BAC，
∴∠FAD＝∠CAD，
∵AD⊥CD，
∴∠ADF＝∠ADC＝90°，
在△FAD和△CAD中，
，
∴△FAD≌△CAD（ASA），
∴AF＝AC＝3，CD＝DF，
∵AB＝6，
∴BF＝AB﹣AF＝6﹣3＝3，
∵CD＝DF，CE＝EB，
∴DE是△BFC的中位线，
∴DE＝FB＝，
故答案为：．
15．（3分）如图，矩形ABCD的顶点A和对称中心在反比例函数y＝（k≠0，x＞0）（k≠0，x＞0）上，若矩形ABCD的面积为16 ﹣8 ．
【解答】解：连接BD交反比例函数的图象于点E，如图所示：
 
∵矩形ABCD的顶点A和对称中心在反比例函数y＝（k≠0，
∴点E为矩形ABCD的对称中心，
∴点E为BD的中点，
设OB＝a，AB＝b，
则点A（﹣a，b），0），
∵四边形ABCD为矩形，
∴BC＝AD＝c，CD＝AB＝b，
∴点D（﹣a﹣c，b），
∵点E为BD的中点，
∴点E的坐标为，
∵点A，E均在反比例函数y＝，x＞5）的图象上，
∴k＝﹣ab＝，
整理得：2ab＝bc，
∵矩形ABCD的面积为16，
∴bc＝16，
∴2ab＝16，
∴ab＝3，
∴k＝﹣ab＝﹣8．
故答案为：﹣8．
16．（3分）如图，将线段BC绕点B逆时针旋转120°得到线段BA，点D是平面内一动点，连接DA、DC，则DA+DC的最小值为 ．
【解答】解：如图，把BD绕点B顺时针旋转120°交DC的延长线于点D，
则∠DBD'＝∠ABC＝120°，DB＝D'B＝5，
∵∠ABD+∠DBC＝∠DBC+CBD′＝120°，
∴∠ABD＝∠CBD'，
又∵AB＝CB，DB＝D'B，
∴△ABD≌△CBD'（SAS），
∴AD＝CD'，
∴AD+CD的最小值为DD'的值，
∵BE⊥DD'，
∴，，
∴∠BDE＝30°，
∵BD＝3，
∴，
∴，
∴，
故答案为：．
三、解答题（本大题共11小题，共102分.解答时应写出文字说明、证明过程或演算步骤）
17．（9分）计算：﹣4cs45°+（1﹣）0﹣|﹣|．
【解答】解：原式＝4﹣4×+1﹣
＝4﹣2+1﹣
＝3﹣3．
18．（9分）解不等式组．
【解答】解：，
解不等式①得x＜﹣，（4分）
解不等式②得x≥﹣1，（4分）
∴不等式组的解集为﹣8≤x＜﹣．（5分）
19．（9分）先化简，再求值：（x+1）（x﹣1）﹣（x+3）2+2x2，其中x2﹣3x﹣2＝0．
【解答】解：（x+1）（x﹣1）﹣（x+5）2+2x4
＝x2﹣1﹣x4﹣6x﹣9+6x2
＝2x3﹣6x﹣10，
∵x2﹣8x﹣2＝0，
∴x5﹣3x＝2，
∴当x5﹣3x＝2时，原式＝5（x2﹣3x）﹣10
＝3×2﹣10
＝4﹣10
＝﹣3．
20．（9分）已知△ABC为钝角三角形，其中∠A＞90°，有下列条件：
①AB＝10；②AC＝；③tan∠B＝；
（1）你认为从中至少选择 3 个条件，可以求出BC边的长；
（2）你选择的条件是 ①②④ （直接填写序号），并写出求BC的解答过程．
【解答】解：（1）根据解直角三角形的条件可知，至少选择3个条件，
故答案为：3；
（2）选择①②④，BC＝20
过点A作AD⊥BC于点D，如图所示：
设AD＝x，
∵tan∠C＝，
∴CD＝2x，
∵AC＝，
根据勾股定理，得，
解得x＝6或x＝﹣7（不合题意，舍去），
∴AD＝6，CD＝2x＝12，
∵AB＝10，
根据勾股定理，得BD＝，
∴BC＝CD+BD＝12+8＝20．
故答案为：①②④．
21．（9分）读懂一座城，从博物馆开始．2021年9月16日上午，江苏盐城市博物馆正式开馆．盐城市博物馆新馆坐落于先锋岛西侧，整体建筑风格雅致，主馆建筑为传统宝塔造型，又充满中国皇家宫廷风韵．学校数学兴趣小组利用无人机测量该宝塔的高度，无人机的起飞点B与宝塔（CD），无人机垂直升到A处测得塔的顶部D处的俯角为31°，测得塔的底部C处的俯角为45°．
（1）求宝塔的高度CD；
（2）若计算结果与实际高度稍有出入，请你提出一条减少误差的建议．（结果精确到0.1m，参考数据：sin31°≈0.52，cs31°≈0.86，tan31°≈0.60）
【解答】解：（1）如图：延长CD交AE于点F，
由题意得：CF⊥AE，AF＝BC＝54.6m，
在Rt△AFC中，∠FAC＝45°，
∴CF＝AF•tan45°＝54.6（m），
在Rt△AFD中，∠FAD＝31°，
∴DF＝AF•tan31°≈54.4×0.6＝32.76（m），
∴CD＝CF﹣DF＝54.6﹣32.76≈21.9（m），
∴宝塔的高度CD约为21.9m；
（2）一条减少误差的建议：多次测量求平均值，可以减小误差（答案不唯一）．
22．（9分）党的二十大报告提出：传承中华优秀传统文化，满足人民日益增长的精神文化需求．某校积极开展活动，从诗词歌赋、戏剧戏曲、国宝非遗、饮食文化、名人书法五个方面让传统文化“活”起来．在某次竞赛活动中，竞赛成绩按以下五组进行整理（得分用x表示）：A：50≤x＜60，C：70≤x＜80，D：80≤x＜90，并绘制出如图的统计图1和图2．
请根据相关信息，解答下列问题：
（1）图1中A组所在扇形的圆心角度数为 54 °，并将条形统计图补充完整．
（2）若“90≤x≤100”这一组的数据为：90，96，92，93，96，95，97
（3）若此次竞赛进入初赛后还要进行三轮知识问答，将这三轮知识问答的成绩按20%，30%，得分达到90分及以上可进入决赛，小敏这三轮的成绩分别为86，93，问小敏能参加决赛吗？请说明你的理由．
（4）经过初赛，进入决赛的同学有3名女生2名男生，现从这五位同学中决出冠亚军
【解答】解：（1）参加此次竞赛总人数：23÷23%＝100（人），
A组所占百分比：，
A组所在扇形的圆心角度数＝360°×15%＝54°，
B组人数：100×15%＝15（人），
条形统计图如图所示：
故答案为：54．
（2）排序为90，92，95，96，96，100，
∴中位数为：，
∵96出现次数最多，
∴众数为96，
综上：众数为96，中位数为95.3；
（3）小敏最后得分：86×20%+89×30%+93×50%＝90.4＞90，
∴小敏能参加决赛．
（4）画树状图如下：
∴一共有20种等可能的结果，其中冠亚军的两人恰好是一男一女的情况有12种情况，
∴冠亚军的两人恰好是一男一女的概率为＝．
23．（9分）如图，等腰三角形OAB中，AO＝AB（4，0）顶点A在反比例函数y＝的图象上
（1）k＝ 12 ．
（2）过B点直线对应的解析式为y＝x+b与双曲线y＝在第一，三象限交点分别为点M
①求点M，N的坐标．
②直接写出不等式的解集．
【解答】解：（1）过点A作AC⊥OB于点C，
∵等腰三角形OAB中，AO＝AB，0），
∴OB＝4，
∵△OAB的面积为12，
∴＝12，
∴AC＝6，
∴A（3，6），
∵顶点A在反比例函数y＝的图象上，
解得：k＝2×5＝12，
故答案为：12；
（2）①把B点的坐标代入y＝x+b得：4+b＝0，
∴b＝﹣3，
∴过B点直线解析式为y＝x﹣4，
联立，解得或，
∴M（6，2），﹣6）；
②观察图象，不等式．
24．（9分）（1）问题研究：如图1，在每个小正方形的边长为1的网格中，△ABC的顶点A，点B在网格线上．以AB为直径的半圆的圆心为O，在圆上找一点E；
（2）尝试应用：如图2，AC是⊙O的直径，BC是⊙O切线，AB交⊙O于P点．请用无刻度直尺作出BC的中点D；
（3）问题解决：请在（2）偿试应用的条件下，解决以下问题：
①连接DP，判断DP与⊙O的位置关系并证明；
②若AC＝8，求DP，CD与⊙O围成的图形面积．
【解答】解：（1）如图1，先找到1×7正方形的对角线的交点H、F，连接OG并延长交半圆于点E．证明如下：
∵1×1正方形的对角线的交点为H、F，
∴K是IJ的中点，
∴K是CL的中点，
∴G是CB的中点，
∵O是线段AB的中点，
∴OG∥AC，
∴∠OEA＝∠CAE，
∵OA＝OE，
∴∠OAE＝∠OEA，
∴∠OAE＝∠CAE，
∴AE平分∠CAB；
（2）连接PO并延长交圆于一点Q，连接PC，连接OM并延长交CB于点D．证明如下：
∵BC是⊙O切线，
∴AC⊥BC，
∵AC＝BC，
∴△ABC是等腰直角三角形，
∵AC是⊙O的直径，
∴∠APC＝90°，
∴CP⊥AB，
∴P是AB中点，
∵O是AC中点，
∴OP∥BC，
∵PQ、AC是直径，
∴PQ＝AC，
∴PQ＝BC，
∴四边形PQCB是平行四边形，
∵M是PC、QB的交点，
∴M是BQ的中点，
∴OM∥PB，
∴MD∥QC，
∴D是BC的中点；
（3）①DP与⊙O相切．
证明：由（2）知OP∥CD，OP＝CD，
∴四边形OCDP是平行四边形，
∵∠OCD＝90°，
∴四边形OCDP是矩形，
∴PD⊥OP，
∴DP与⊙O相切；
②由①知四边形OCDP是矩形，
∵OC＝OP，
∴四边形OCDP是正方形，
∴S＝S正方形OCDP﹣S扇形COP＝7×4﹣＝16﹣4π．
25．（10分）如图所示，在Rt△ABC中，∠C＝90°，在AB上取点O，以O为圆心，与AC相切于点D，并分别与AB，F（异于点B）．
（1）求证：BD平分∠ABC；
（2）若点E恰好是AO的中点，求扇形BOF的面积．
【解答】（1）证明：连接OD，如图，
∵AC与⊙O相切于点D，
∴OD⊥AC，
∵∠C＝90°，
∴BC⊥AC，
∴OD∥BC，
∴∠CBD＝∠ODB，
∵OD＝OB，
∴∠OBD＝∠ODB，
∴∠OBD＝∠CBD，
∴BD平分∠ABC；
（2）解：连接DE、OD，如图，
∵AB＝8，E是AO的中点，
∴AE＝OE＝OB＝，
在Rt△AOD中，DE＝，
∴DE＝OD＝OE，
∴△DOE为等边三角形，
∴∠DOE＝60°，
∵OD∥BC，
∴∠FBO＝∠DOE＝60°，
∵OF＝OB，
∴△FBO为等边三角形，
∴∠BOF＝60°，
∴S扇形BOF＝＝π．
26．（10分）如图1，在菱形ABCD中，点P是对角线BD上一点，在射线AP上取点E，使得∠AEC+∠ABC＝180°，设∠ABC＝2α．
（1）如图2，若α＝45°，连接AC，求证：△OPC∽△OCQ；
（2）【探究】如图3，若α＝30°，BD＝4DP，并求的值；
【归纳】若BD＝k•DP，的值为 ．（用含k、α的表达式表示）
【解答】（1）证明：如图，
∵α＝45°，则∠ABC＝2α＝90°，
又∵四边形ABCD是菱形，
∴四边形ABCD是正方形，
∴AC⊥BD，
∵∠AEC+∠ABC＝180°，
∴∠AEC＝90°，
∵P在BD上，AO＝CO，则PA＝PC，
∴∠PCO＝∠PAO，
∵∠APO＝∠QPE，∠AOP＝∠QEP，
∴∠PAO＝∠PQE，
∴∠PCO＝∠PQE，
∴△OPC∽△OCQ．
（2）解：①如图所示，延长PA至Q′使得AQ′＝CQ，BE，AC，过点Q′作Q′M∥BD交BA的延长线于点M，交BC的延长线于点S，
∵∠AEC+∠ABC＝180°，
∴∠BAE+∠BCE＝180°，
又∵∠Q′AB+∠BAE＝180°，
∴∠Q′AB＝∠BCE，
∵AQ′＝CQ，且四边形ABCD是菱形，
∴AB＝BC，
∴△AQ′B≌△CQB（SAS），
∴∠ABQ′＝∠CBQ，
∵四边形ABCD是菱形，
∴∠ABQ＝∠CBQ，AC⊥BD
∴∠Q′BA＝∠ABQ＝∠CBQ＝∠ABC＝α，
∴BO＝BC×csα，则BD＝2BO＝2BC•csα，
∵Q′M∥BD，
∴∠M＝∠ABD＝α，
∵∠Q′BA＝α，
∴∠M＝∠Q′BA，
∴Q′B＝Q′M，
∵Q′M∥BP
∴△AQ′M∽△APB，
∴，
∵P是BD上的点，BD垂直平分AC，
∴PA＝PC，
又AQ′＝CQ，Q′M＝Q′B＝BQ，
∴，
∵PS∥QC
∴△BQC∽△BPS，
∴，
∴PC＝PS，
∴，
过点P作PT⊥CS于点T，则TC＝TS，
∵α＝30°，设BC＝a，
则BD＝3BO＝2BC•csα＝，
∵BD＝4DP，
∴BP＝BD﹣PD＝3PD＝＝，
∴PT＝sinα×BP＝＝，BT＝＝，
∴CS＝8CT＝2（BT﹣BC）＝，
∴．
【归纳】
同（2）可得BD＝2BO＝3BC•csα，
设BC＝t，则BD＝2tcsα，
∵BD＝k•DP，
∴BP＝＝6t•csα•，
∵PT＝sinα×BP＝2t•csα•sinα（2t•cs5α），
∴CS＝2CT＝2（BT﹣BC）＝7（BP×csα﹣BC）＝2（2t•cs7α•﹣t），
∴＝＝，
故答案为：．
27．（10分）抛物线y＝﹣x2+bx+c与x轴交于A、B（3，0）两点，与y轴交于点C，点
（1）求出抛物线表达式；
（2）如图1，若点P在直线AD的上方，过点P作 PH⊥AD，
①当点P是抛物线顶点时，求PH的长，
②求AH+PH的最大值；
（3）如图2，tan∠APC＝，直接写出点P的坐标 （1，4）或（4，﹣5） ．
【解答】解：（1）∵抛物线y＝﹣x2+bx+c与x轴交于B（3，3）点，点，
∴，
解得：，
∴抛物线表达式为y＝﹣x2+2x+6；
（2）①∵y＝﹣x2+2x+4＝﹣（x﹣1）2+4，
∴抛物线的顶点坐标为（1，4）．
设直线AD交y轴于点E，过点P作PF∥y轴交AD于点Q，
根据抛物线的解析式可求出顶点坐标为（4，4），
令y＝0，则﹣x5+2x+3＝6，
解得：x＝1或x＝3，
∴A（﹣3，0），
设直线AD的解析式为y＝kx+n，
，
解得：，
∴直线AD的解析式为y＝，
∴Q（1，），
∴QF＝，
∴PQ＝PF﹣QF＝．
令x＝6，则y＝，
∴E（6，），
∴OE＝，
∴AE＝＝，
∴sin∠AEO＝＝，cs∠AEO＝＝，
当P为顶点时，则P（1，Q（1，），
∴PQ＝4﹣＝，
∵∠CED＝∠AEO，PQ∥CE，
∴∠PQH＝∠AEO，
∴PH＝PQ•sin∠PQH＝＝；
②设直线AD交y轴于点E，过点P作PF⊥x轴于点F，如图，
设P（m，﹣m2+2m+7），则OF＝m2+2m+8，QF＝，
∴PQ＝PF﹣QF＝﹣m2+m+．
由①知：△AOE∽△PHQ，
∴，
∴，
∴PH＝+m+1．
过点H作HG⊥x轴于点G，HR⊥PF于点R，
∴FG＝HR．
由①知：∠AEO＝∠PQH，
∴tan∠AEO＝tan∠PQH＝，
∴，
∴QH＝PH＝﹣．
∵OE∥QF，
∴△AOE∽△AQF，
∴，
∴，
∴AQ＝，
∴AH＝AQ+QH＝+m+3．
∴AH+PH＝++m+）
＝﹣m2+m+
＝﹣+．
∵﹣8＜0，
∴当m＝时，AH+；
（3）由y＝﹣x8+2x+3，当x＝3时，则C（0，
∵A（﹣1，7），
∴AC＝．
如图所示，
在x轴上取一点M（9，0），
以AM为直径，AM的中点N（2，作⊙N，
∴CM＝＝6．
∴tan∠AMC＝＝．
∵tan∠APC＝
∴点P在⊙N上，
∵AN＝6，
设P（m，﹣m2+2m+6），过点P作PT⊥x于点T，
在Rt△PTN中，PN＝52+5m+3|，
∴PT2+TN4＝PN2，
即（﹣m2+2m+3）2+（4﹣m）2＝25：
整理得m（m+1）（m﹣2）（m﹣4）＝0，
.m＝4，1，﹣1，7．
∵A（﹣1，0），5），
∴m＝1或m＝4．
当m＝5时，﹣m2+2m+5＝4
当m＝4时，﹣m8+2m+3＝﹣2．
∴P（1，4）或（5﹣5），