陕西省延安市志丹县2023-2024学年七年级下学期月考数学试卷(含答案)

这是一份陕西省延安市志丹县2023-2024学年七年级下学期月考数学试卷(含答案)，共14页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

一、单选题
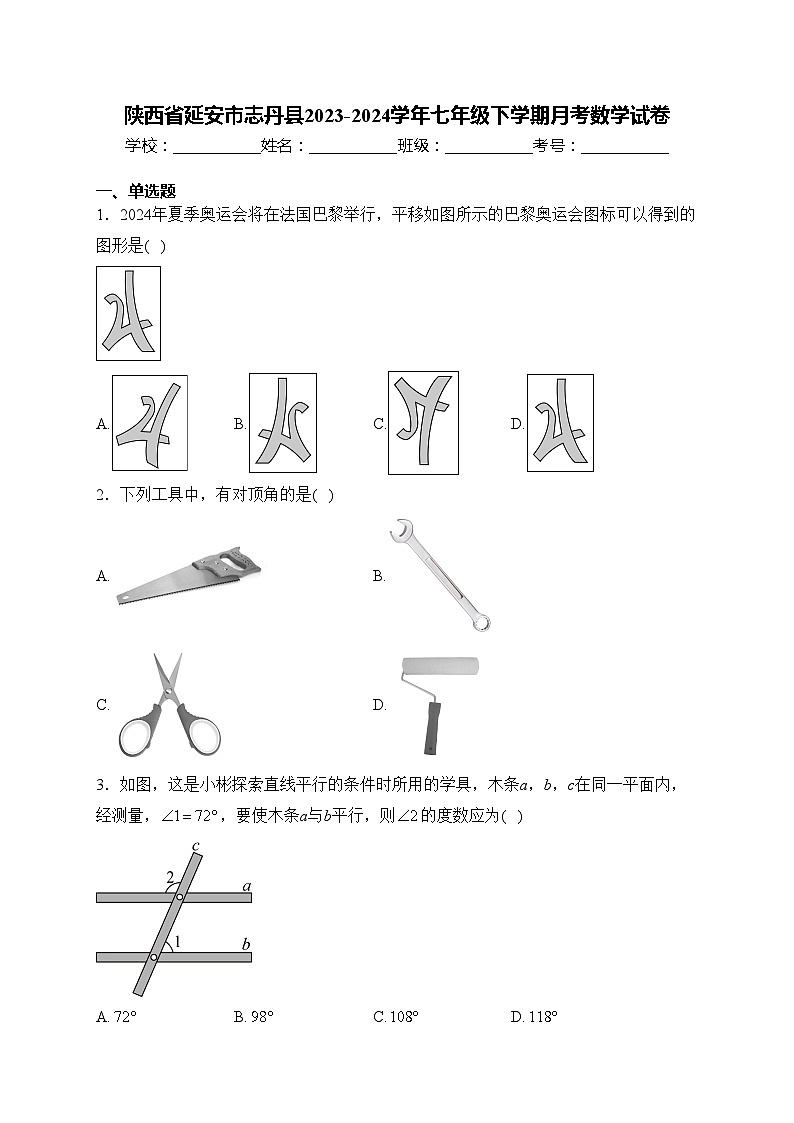
1．2024年夏季奥运会将在法国巴黎举行，平移如图所示的巴黎奥运会图标可以得到的图形是( )
A.B.C.D.
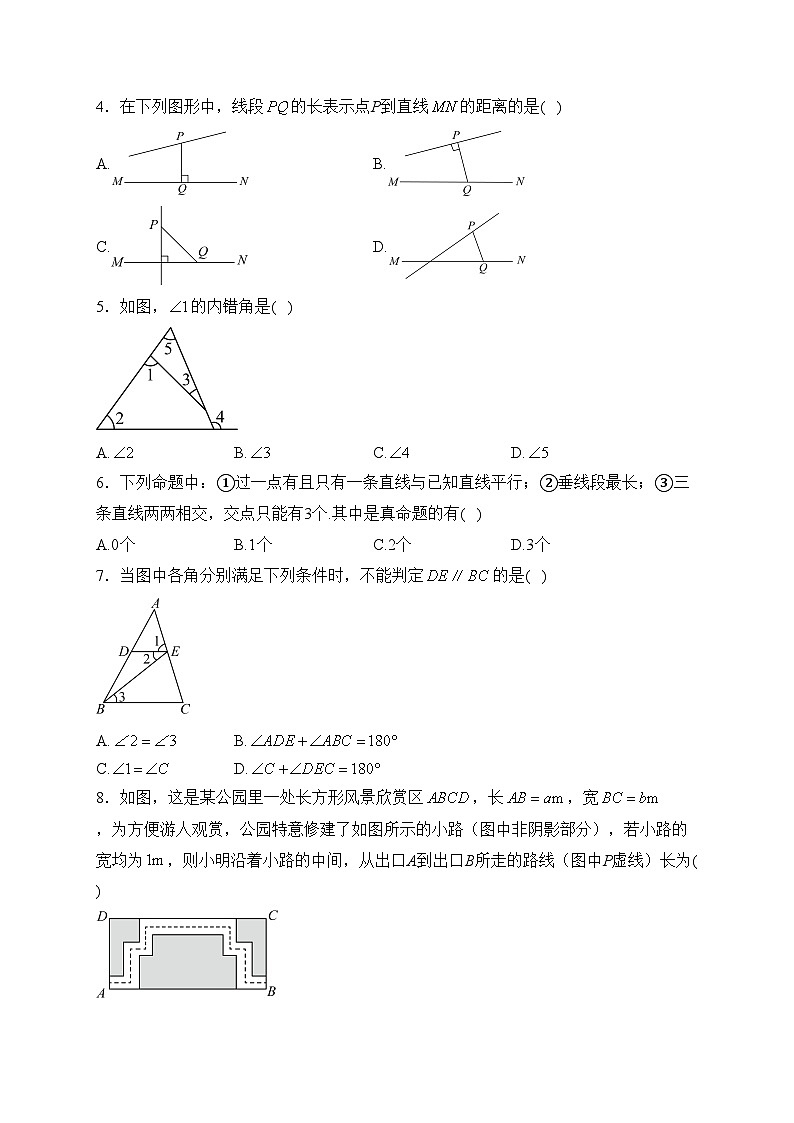
2．下列工具中，有对顶角的是( )
A.B.
C.D.
3．如图，这是小彬探索直线平行的条件时所用的学具，木条a，b，c在同一平面内，经测量，，要使木条a与b平行，则的度数应为( )
A.B.C.D.
4．在下列图形中，线段的长表示点P到直线的距离的是( )
A.B.
C.D.
5．如图，的内错角是( )

A.B.C.D.
6．下列命题中：①过一点有且只有一条直线与已知直线平行；②垂线段最长；③三条直线两两相交，交点只能有3个.其中是真命题的有( )
A.0个B.1个C.2个D.3个
7．当图中各角分别满足下列条件时，不能判定的是( )

A.B.
C.D.
8．如图，这是某公园里一处长方形风景欣赏区，长，宽，为方便游人观赏，公园特意修建了如图所示的小路（图中非阴影部分），若小路的宽均为，则小明沿着小路的中间，从出口A到出口B所走的路线（图中P虚线）长为( )
A.B.C.D.
二、填空题
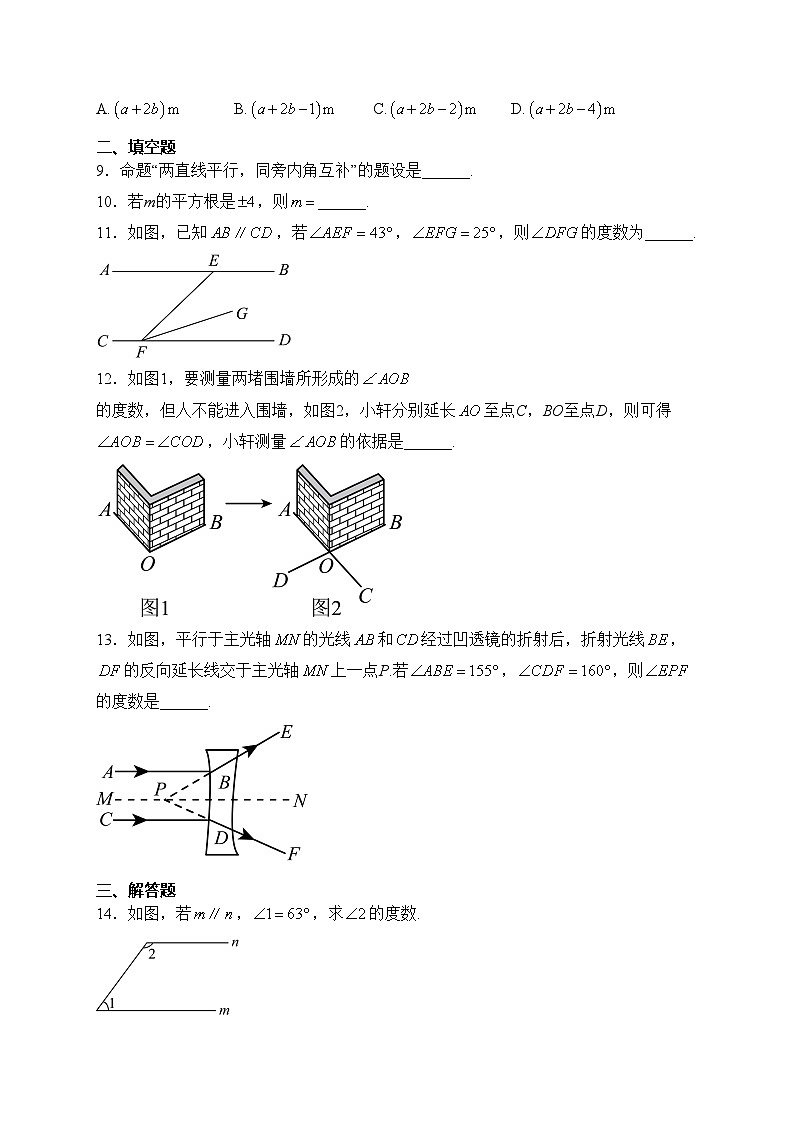
9．命题“两直线平行，同旁内角互补”的题设是______.
10．若m的平方根是，则______.
11．如图，已知，若，，则的度数为______.
12．如图1，要测量两堵围墙所形成的的度数，但人不能进入围墙，如图2，小轩分别延长至点C，BO至点D，则可得，小轩测量的依据是______.
13．如图，平行于主光轴的光线和经过凹透镜的折射后，折射光线，的反向延长线交于主光轴上一点P.若，，则的度数是______.
三、解答题
14．如图，若，，求的度数.
15．如图，直线，相交于点O，平分，若，求的度数.
16．如图，，若，求的度数.
17．如图，已知，求的度数.
18．如图，已知：，与相交于点E，且.求证：.
19．如图，若，，，求的度数.
20．如图，，，，，求的度数.
21．完成下面的证明过程.
已知：如图，点在上，与交于点.
求证：.
证明：（已知），
（____________）
（已知），
______（______），
______（____________），
（____________）.
22．如图，，.
(1)求证：；
(2)若，，求的度数.
23．已知，.
(1)若x的算术平方根为3，求a的值.
(2)若一个正数的两个平方根分别为x，y，求这个正数.
24．课本再现
（1）如图1，一条公路两次转弯后，和原来的方向相同.如果第一次的拐角是，第二次的拐角是多少度？为什么？
拓展延伸
（2）如图2，一条公路修到湖边时，需拐弯绕湖而过，若第一次拐角，第二次拐角，第三次拐的角是，这时的道路恰好和第一次拐弯之前的道路平行，求的度数.
25．图1是一辆滑轮摄影轨道车，图2为其侧面示意图.固定在底座于点，与是轨道车的“手臂”，可通过改变的度数调节车的高度.在调节过程中，放摄像机的杆始终平行于.
(1)如图3，调节轨道车的“手臂”，使，此时，求的度数.
(2)若图2中，求与的度数之和.
26．综合与实践
问题提出
如图1，已知，M，N分别是上的两点.点P在之间.探究、与之间的数量关系.
初步感知
（1）求证：.
延伸应用
（2）如图2，平分，且与的延长线交于点Q，平分，平分，，若，求的度数.
参考答案
1．答案：D
解析：由图形可知，选项D与原图形完全相同.
故选：D
2．答案：C
解析：由对顶角的定义可知，下列工具中，有对顶角的是选项C.
故选：C.
3．答案：C
解析：∵，
∴，
∵，
∴，
∴，
故选：C.
4．答案：A
解析：因为A选项中垂直于，所以线段的长表示点P到直线的距离的是A选项.
故选：A.
5．答案：B
解析：如图：根据内错角、同旁内角、同位角的定义可得：的内错角是，的同旁内角是，的同位角是.
故选B.
6．答案：A
解析：①过直线外一点有且只有一条直线与已知直线平行，原命题是假命题；
②垂线段最短，原命题是假命题；
③三条直线两两相交，交点有3个或者1个，原命题是假命题；
∴真命题有0个，
故选：A.
7．答案：B
解析：A、∵，∴，不符合题意；
B、∵，不能得到，符合题意；
C、∵，∴，不符合题意；
D、∵，∴，不符合题意；
故选：B.
8．答案：D
解析：利用已知可以得出此图形可以分为横向与纵向分析，横向距离等于，纵向距离等于，
∵，，
∴小明沿着小路的中间，从出口A到出口B所走的路线（图中P虚线）长为，
故选：D.
9．答案：两直线平行
解析：命题“两直线平行，同旁内角互补”的题设是两直线平行，结论是同旁内角互补，
故答案为两直线平行.
10．答案：16
解析：由题意知：，
解得：，
故答案为：16.
11．答案：
解析：∵，
∴，
∵，且，
∴，
故答案为：.
12．答案：对顶角相等
解析：由题意得，小轩测量的依据是对顶角相等，
故答案为：对顶角相等.
13．答案：
解析：∵，，
∴，.
∵，，
∴，，
∴.
故答案为：.
14．答案：
解析：∵，
∴.
∵，
∴
15．答案：
解析：平分，，
，
.
16．答案：
解析：∵，
∴，
∴，
∵，
∴.
17．答案：
解析：∵，，
∴，
∴.
18．答案：见解析
解析：证明：因为，
所以（两直线平行，内错角相等）
又因为，
所以，
所以.（同位角相等，两直线平行）
19．答案：的度数为
解析：如图所示，
∵，，
∴，，
∴，
∴，
∵，
∴，
∴的度数为：.
20．答案：
解析：∵，，
∴，
∴，，
∵，
∴，
∴，
∴.
21．答案：两直线平行，内错角相等；；等量代换；；同位角相等，两直线平行；两直线平行，同位角相等
解析：证明：（已知），
（两直线平行，内错角相等）
（已知），
（等量代换），
（同位角相等，两直线平行），
（两直线平行，同位角相等）.
22．答案：(1)见解析
(2)
解析：（1）证明：，
，
，
，
；
（2），，
，
∵，
∴，
∵，
∴.
23．答案：(1)
(2)25
解析：（1）依题意，∵x的算术平方根为3，
∴，
即，
∴.
（2）根据题意得，
即，
∴，
∴，
∴这个正数为.
24．答案：(1)，两直线平行，内错角相等
(2)的度数为
解析：（1）∵两次转弯后，和原来的方向相同，如图所示，
∴，且，
∴，两直线平行，内错角相等；
（2）∵第三次拐，这时的道路恰好和第一次拐弯之前的道路平行，如图所示，即，过点作，
∴，
∴，
∵，
∴，
∴，
∴的度数为.
25．答案：(1)
(2)
解析：（1）如图1，过点作，且点在的下方.
∵，，
∴.
∵，
∴，
∴，
∴.
∵，，
∴，
∴.
（2）如图2，过点作，且点在的下方.
∵，
∴.
由（1）可得，
∴.
∵，
∴，
∴.
26．答案：（1）详见解析
（2）
解析：（1）证明：如图，过点P作，且点E在点P的左侧.
∵
∴，
∴，.
∵，
∴.
（2）设，则.
由（1）得，
∴.
∵NQ平分，NT平分，
∴.
∵，
∴，
∴，
解得，
∴.
∵MT平分，
∴.
∵，
∴.