

2023-2024学年江苏省南京一中八年级(下)月考数学试卷(3月份)(含解析)
展开
这是一份2023-2024学年江苏省南京一中八年级(下)月考数学试卷(3月份)(含解析),共19页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
1.下列图案中,既是中心对称图形又是轴对称图形的是( )
A. B.
C. D.
2.某市有47857名初中毕业生参加升学考试,为了了解这47857名考生的数学成绩,从中抽取2000名考生的数学成绩进行统计,在这个问题中样本是( )
A. 47857名考生的数学成绩B. 2000
C. 抽取的2000名考生D. 抽取的2000名考生的数学成绩
3.甲校女生占全校总人数的54%,乙校女生占全校总人数的50%,则女生人数( )
A. 甲校多于乙校B. 甲校少于乙校C. 不能确定D. 两校一样多
4.下列运算中,正确的是( )
A. 2+ 3= 5B. 2 2− 2= 2
C. (−2)×(−3)= −2× −3D. 6÷ 3= 3
5.矩形具有而平行四边形不一定具有的性质是( )
A. 对角线互相垂直B. 对角线相等C. 对角线互相平分D. 对角相等
6.如图,线段AB与线段CD关于点P对称,若点A(a,b)、B(5,1)、D(−3,−1),则点C的坐标为( )
A. (−a,−b)
B. (−a+2,−b)
C. (−a−1,−b+1)
D. (−a+1,−b−1)
二、填空题:本题共10小题,每小题3分,共30分。
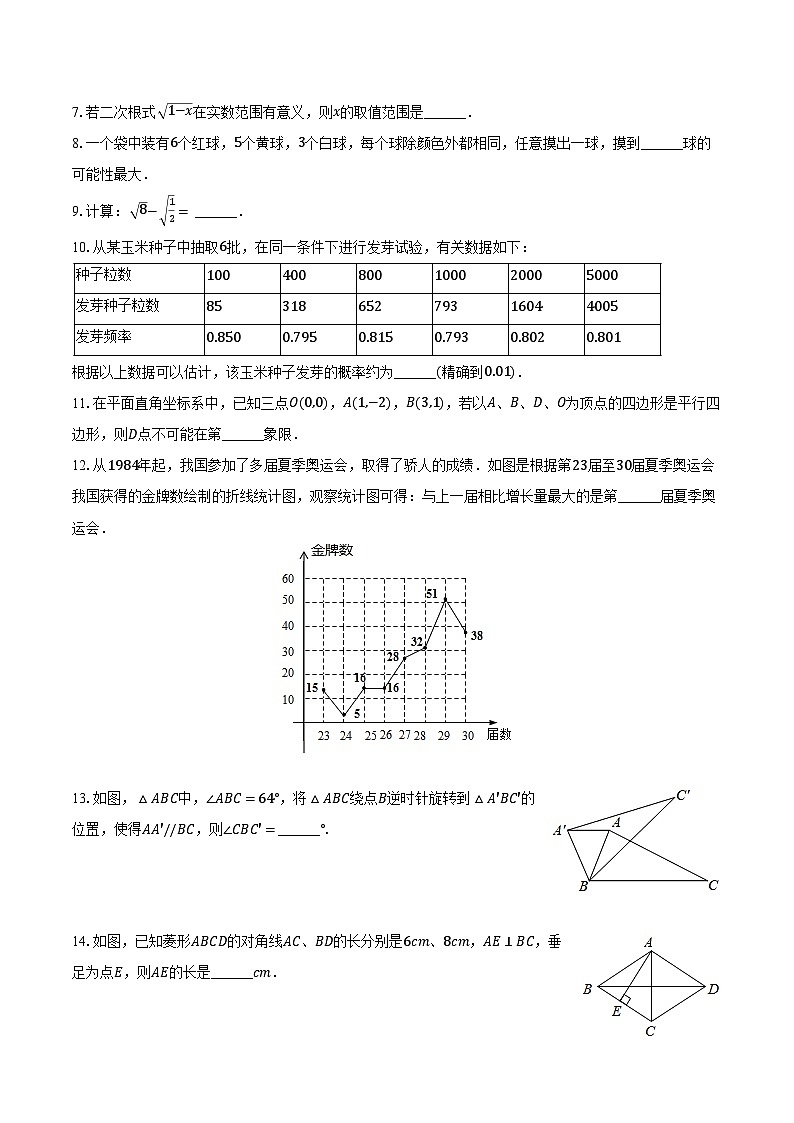
7.若二次根式 1−x在实数范围有意义,则x的取值范围是______.
8.一个袋中装有6个红球,5个黄球,3个白球,每个球除颜色外都相同,任意摸出一球,摸到______球的可能性最大.
9.计算: 8− 12= ______.
10.从某玉米种子中抽取6批,在同一条件下进行发芽试验,有关数据如下:
根据以上数据可以估计,该玉米种子发芽的概率约为______(精确到0.01).
11.在平面直角坐标系中,已知三点O(0,0),A(1,−2),B(3,1),若以A、B、D、O为顶点的四边形是平行四边形,则D点不可能在第______象限.
12.从1984年起,我国参加了多届夏季奥运会,取得了骄人的成绩.如图是根据第23届至30届夏季奥运会我国获得的金牌数绘制的折线统计图,观察统计图可得:与上一届相比增长量最大的是第______届夏季奥运会.
13.如图,△ABC中,∠ABC=64°,将△ABC绕点B逆时针旋转到△A′BC′的位置,使得AA′//BC,则∠CBC′=______°.
14.如图,已知菱形ABCD的对角线AC、BD的长分别是6cm、8cm,AE⊥BC,垂足为点E,则AE的长是______cm.
15.如图,在矩形ABCD中,AC、BD交于点O,DE⊥AC于点E,若∠AOD=110°,则∠CDE=______°.
16.如图,在△ABC中,AB=2,AC= 2,∠BAC=105°,△ABD、△ACE、△BCF都是等边三角形,则四边形AEFD的面积为______.
三、解答题:本题共9小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.(本小题10分)
计算:
(1)1 2−4 12+ 27+3 8;
(2)(2 12− 13)× 6.
18.(本小题8分)
已知:如图,在▱ABCD中,点E、F分别在AD、BC上,且∠ABE=∠CDF.
求证:四边形BFDE是平行四边形.
19.(本小题8分)
今年4月23日是第23个“世界读书日”.某校围绕学生日人均阅读时间这一问题,对初二学生进行随机抽样调查.如图是根据调查结果绘制成的统计图(不完整),请你根据图中提供的信息解答下列问题:
(1)本次抽样调查的样本容量是多少?
(2)请将条形统计图补充完整.
(3)在扇形统计图中,计算出日人均阅读时间在1~1.5小时对应的圆心角度数.
(4)根据本次抽样调查,试估计我市12000名初二学生中日均阅读时间在0.5~1.5小时的有多少人.
20.(本小题7分)
某中学八年级共有10个班,每班40名学生,学校对该年级学生数学学科某次学情调研测试成绩进行了抽样分析,请按要求回答下列问题:
(1)若要从全年级学生中抽取40人进行调查,你认为以下抽样方法中最合理的是______;
①随机抽取一个班级的40名学生的成绩;
②在八年级学生中随机抽取40名女学生的成绩;
③在八年级10个班中每班各随机抽取4名学生的成绩.
(2)将抽取的40名学生的成绩进行分组,绘制如下成绩频数分布表:
①m= ______,n= ______;
②根据表格中的数据,请用扇形统计图表示学生成绩分布情况.
八年级部分学生数学成绩频数分布表
21.(本小题6分)
如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,A(−1,4),B(−4,1),解答下列问题:
(1)将线段AB绕原点O顺时针方向旋转90°得到线段CD,再将线段CD向下平移2个单位长度得到线段EF,画出线段CD和线段EF;
(2)如果线段AB旋转可以得到线段EF,则旋转中心P的坐标为______.
22.(本小题7分)
如图,菱形ABCD的对角线相交于O点,DE//AC,CE//BD.
(1)求证:四边形OCED是矩形;
(2)若AD=5,BD=8,计算DE的值.
23.(本小题8分)
如图,四边形ABCD是平行四边形,E为AB上任意一点.
(1)如图①,只用无刻度的直尺在CD边上作出点F,使DF=BE;
(2)如图②,用直尺和圆规作出菱形EFGH,使得点F、G、H分别在边BC、CD、DA上.(不写作法,只保留作图痕迹)
24.(本小题8分)
如图,在▱ABCD中,E,F分别为AD,BC的中点,AG⊥BD,CH⊥BD,垂足分别为G,H,连接EG,EH,FG,FH.
(1)求证:四边形GEHF是平行四边形;
(2)若AB=2,BC=3,当BD=______时,▱GEHF是矩形.
25.(本小题10分)
在矩形ABCD中,P是线段BC上的一个动点,将△ABP沿直线AP翻折,点B的对应点为E,直线PE与直线AD交于点F.
(1)如图①,当点F在AD的延长线上时,求证:AF=PF;
(2)若AB=6,BC足够长,当点E到直线AD的距离等于3时,求BP的长;
(3)若AB=6,BC=10,当点P、E、D在同一直线上(如图②)时,点P开始向点C运动,到与C重合时停止,则点F运动的路程是______.
答案和解析
1.【答案】A
【解析】解:A、该图形既是轴对称图形,也是中心对称图形,符合题意;
B、该图形既不是轴对称图形,也不是中心轴对称图形,不符合题意;
C、该图形不是中心对称图形,是轴对称图形,不符合题意;
D、该图形不是中心对称图形,是轴对称图形,不符合题意;
故选:A.
根据中心对称图形的定义和轴对称图形的定义,对选项逐个判断,即可判断出答案.
此题考查了中心对称图形和轴对称图形的概念,掌握相关概念是解题的关键,图形绕一点旋转180°后能够与原图形完全重合则此图形为中心对称图形;轴对称图形的定义:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴.
2.【答案】D
【解析】解:这个问题中样本是所抽取的2000名考生的数学成绩.
故选:D.
根据样本的定义:从总体中取出的一部分个体叫做这个总体的一个样本进行解答即可.
本题考查了总体、个体、样本和样本容量:我们把所要考察的对象的全体叫做总体;把组成总体的每一个考察对象叫做个体;从总体中取出的一部分个体叫做这个总体的一个样本;一个样本包括的个体数量叫做样本容量.
3.【答案】C
【解析】解:两个学校的总人数不能确定,故甲校女生和乙校女生的人数不能确定.
故选:C
这里甲校与乙校的总人数不确定,所以甲校女生人数与乙校女生人数也不能确定,所以没法比较她们人数的多少.
本题考查频率问题,关键在于:只有确定两个学校的总人数才能进行比较.
4.【答案】B
【解析】解: 2+ 3不能合并成一项,故选项A错误,
∵2 2− 2= 2,故选项B正确,
∵负数没有算术平方根,故选项C错误,
∵ 6÷ 3= 2,故选项D错误,
故选:B.
根据各个选项中的式子可以计算出正确的结果,从而可以解答本题.
本题考查二次根式的混合运算,解答本题的关键是明确二次根式混合运算的计算方法.
5.【答案】B
【解析】【分析】
本题考查矩形的性质,矩形具有平行四边形的性质,又具有自己的特性,要注意运用矩形具备而一般平行四边形不具备的性质.如,矩形的对角线相等.矩形的对角线互相平分且相等,而平行四边形的对角线互相平分,不一定相等.
【解答】
解:矩形的对角线相等,而平行四边形的对角线不一定相等.
故选B.
6.【答案】B
【解析】解:∵线段AB与线段CD关于点P对称,
点P为线段AC、BD的中点.
∴a+m2=5−32,b+n2=1−12,
∴m=2−a,n=−b,
∴B(2−a,−b),
故选:B.
运用中点坐标公式求答案.
本题考查了中心对称,正确运用中点坐标公式是解题的关键.
7.【答案】x≤1
【解析】解:由题意得:1−x≥0,
解得:x≤1.
故答案为:x≤1.
根据二次根式有意义的条件可得1−2≥0,再解即可.
本题考查了二次根式有意义的条件,掌握二次根式中的被开方数是非负数是关键.
8.【答案】红
【解析】解:∵袋中装有6个红球,5个黄球,3个白球,
∴总球数是:6+5+3=14个,
∴摸到红球的概率是=614=37;
摸到黄球的概率是514;
摸到白球的概率是314;
∴摸出红球的可能性最大.
故答案为:红.
先求出总球的个数,再分别求出摸出各种颜色球的概率,即可比较出摸出何种颜色球的可能性最大.
本题主要考查可能性的大小,只需求出各自所占的比例大小即可,求比例时,应注意记清各自的数目.
9.【答案】32 2
【解析】解:原式=2 2− 22=3 22.
首先将各二次根式化为最简二次根式,再合并同类二次根式即可.
在二次根式的加减运算中,首先要将各式化为最简二次根式,然后再合并同类二次根式,不是同类二次根式的不能合并.
10.【答案】0.80
【解析】解:观察表格得到这种玉米种子发芽的频率稳定在0.801附近,
0.801≈0.80,
则这种玉米种子发芽的概率约是0.80.
故答案为0.80.
观察表格得到这种玉米种子发芽的频率稳定在0.801附近,即可估计出这种玉米种子发芽的概率.
本题考查了利用频率估计概率,以及频数(率)分布表.
11.【答案】二
【解析】解:如图所示:以A、B、D、O为顶点的四边形是平行四边形,
则D点不可能在第二象限.
故答案为:二.
直接利用平行四边形的判定方法结合其坐标位置,进而得出符合题意的答案.
此题主要考查了平行四边形的判定以及坐标与图形的性质,正确利用数形结合分析是解题关键.
12.【答案】29
【解析】解:观察统计图可得:与上一届相比增长量最大的是第29届夏季奥运会.
故答案为:29.
根据折线统计图反映了变化趋势,观察图形,即可得出增长幅度最大的年份和增加额.
此题考查了折线统计图,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键,折线统计图表示的是事物的变化情况.
13.【答案】52
【解析】解:∵△ABC绕点A逆时针旋转得到△BA′C′,
∴BA′=AB,
∴∠BAA′=∠BA′A,
∵AA′//BC,
∴∠A′AB=∠ABC,
∵∠ABC=64°,
∴∠A′AB=64°,
∴∠ABA′=(180°−2×64°)=52°,
∵∠CBC′=∠ABA′,
∴∠CBC′=52°.
故答案为:52.
首先根据旋转的性质可知BA′=AB,即可得到∠BAA′=∠BA′A,由AA′//BC,得到∠A′AB=64°,再由三角形内角和定理得到∠ABA′的度数,即可得到∠CBC′的度数.
本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.
14.【答案】245
【解析】解:如图,设AC与BD的交点为O,
∵四边形ABCD是菱形,
∴CO=12AC=3cm,BO=12BD=4cm,AC⊥BD,
∴BC= BO2+CO2= 9+16=5cm,
∴S菱形ABCD=12AC⋅BD=12×6×8=24(cm2),
∵S菱形ABCD=BC×AE,
∴BC×AE=24,
∴AE=245(cm),
故答案为:245.
根据菱形的性质得出BO、CO的长,在Rt△BOC中求出BC,利用菱形面积等于对角线乘积的一半,也等于BC×AE,可得出AE的长度.
此题考查了菱形的性质,以及勾股定理,关键是掌握菱形的面积的两种表示方法,菱形的对角线互相垂直且平分.
15.【答案】35
【解析】解:∵四边形ABCD是矩形,
∴∠ADC=90°,AC=BD,OA=OC,OB=OD,
∴OC=OD,
∴∠ODC=∠OCD,
∵∠AOD=110°,
∴∠DOE=70°,∠ODC=∠OCD=12(180°−70°)=55°,
∵DE⊥AC,
∴∠ODE=90°−∠DOE=20°,
∴∠CDE=∠ODC−∠ODE=55°−20°=35°;
故答案为:35.
由矩形的性质得出OC=OD,得出∠ODC=∠OCD=55°,由直角三角形的性质求出∠ODE=20°,即可得出答案.
本题主要考查了矩形的性质、等腰三角形的性质以及直角三角形的性质等知识;熟练掌握矩形的性质和等腰三角形的性质是解题的关键.
16.【答案】2
【解析】【分析】
本题综合考查了平行四边形的判定与性质,全等三角形的判定与性质以及等边三角形的性质.综合性比较强,难度较大,有利于培养学生综合运用知识进行推理和计算的能力.根据题中的等式关系可推出两组对边分别相等,从而可判断四边形AEFD为平行四边形,求出∠DAE=135°,易得∠FDA=45°,所以由平行四边形的面积公式即可解答.
【解答】
解:∵△ABD,△ACE都是等边三角形,
∴∠DAB=∠EAC=60°,
∵∠BAC=105°,
∴∠DAE=135°,
∵△ABD和△BCF都是等边三角形,
∴∠DBF+∠FBA=∠ABC+∠FBA=60°,
∴∠DBF=∠ABC.
在△ABC与△DBF中,
BD=BA∠DBF=∠ABCBF=BC
∴△ABC≌△DBF(SAS),
∴AC=DF=AE= 2,
同理可证△ABC≌△EFC,
∴AB=EF=AD=2,
∴四边形AEFD是平行四边形(两组对边分别相等的四边形是平行四边形).
∴∠FDA=180°−∠DAE=45°,
∴AD边上的高h等于1,
∴S▱AEFD=AD⋅h=2×1=2.
即四边形AEFD的面积是2,
故答案为2.
17.【答案】解:(1)原式= 22−2 2+3 3+6 2
=9 22+3 3;
(2)原式=2 2×6×6− 13×6
=12 2− 2
=11 2.
【解析】(1)先把各二次根式化为最简二次根式,然后合并同类二次根式即可;
(2)先根据二次根式的乘法法则运算,然后化简二次根式后合并即可.
本题考查了二次根式的混合运算,熟练掌握二次根式的性质、二次根式的乘法法则是解决问题的关键.
18.【答案】证明:∵四边形ABCD为平行四边形,
∴AD//BC,∠ABC=∠ADC,
∴∠ADF=∠DFC,ED//BF,
∵∠ABE=∠CDF,
∴∠EBC=∠ADF,
∴∠EBC=∠DFC,
∴EB//DF,
∵ED//BF,
∴四边形BFDE是平行四边形.
【解析】证明EB//DF,可得结论.
此题考查了平行四边形的性质与判定,注意熟练掌握定理与性质是解决问题的关键.
19.【答案】解:(1)30÷20%=150,
即样本容量是150;
(2)日人均阅读时间在0.5~1小时的人数是:150−30−45=75(人),
补全的条形统计图如右图所示;
(3)人均阅读时间在1~1.5小时对应的圆心角度数是:360°×45150=108°;
(4)12000×75+45150=9600(人),
答:我市12000名初二学生中日均阅读时间在0.5~1.5小时的有9600人.
【解析】本题考查条形统计图、扇形统计图、样本容量、用样本估计总体,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.
(1)根据统计图中的数据可以求得样本容量;
(2)根据(1)中的结果可以求得阅读时间在0.5~1小时的人数,从而可以将条形统计图补充完整;
(3)根据统计图中的数据可以求得日人均阅读时间在1~1.5小时对应的圆心角度数;
(4)根据统计图中的数据可以估计我市12000名初二学生中日均阅读时间在0.5~1.5小时的有多少人.
20.【答案】③ 16 0.2
【解析】解:(1)由题意可得,
抽样方式最合理的是在八年级10个班中每班各随机抽取4名学生的成绩;
故答案为:③;
(2)①m=40×0.4=16;
n=840=0.2;
故答案为:16,0.2;
②根据各类的频率画图如下:
(1)根据各个小题中的说法可以选除最合理的一个;
(2)①根据频数、频率与总数之间的关系求出m和n;
②根据图表中的频率即可画出扇形统计图.
本题考查扇形统计图及相关计算.在扇形统计图中,每部分占总部分的百分比等于该部分所对应的扇形圆心角的度数与360°的比.
21.【答案】(−1,−1)
【解析】解:(1)如图,线段CD和线段EF即为所求;
(2)线段AB绕点P(−1,−1)顺时针旋转90°可以得到线段EF,
所以P(−1,−1).
(1)根据旋转和平移的性质即可画出线段CD和线段EF;
(2)根据对应点连线的垂直平分线的交点就是旋转中心,将线段AB绕点P(−1,−1)顺时针旋转90°即可以得到线段EF.
本题考查了作图−旋转变换,作图−平移变换,解决本题的关键是掌握旋转和平移的性质.
22.【答案】(1)证明:∵DE//AC,CE//BD,
∴四边形OCED是平行四边形,
∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠DOC=90°,
∴四边形OCED是矩形;
(2)解:∵四边形ABCD是菱形,BD=8,
∴OD=12BD=4,OC=OA,AD=CD,
∵AD=5,
∴OC= 52−42=3,
∵四边形OCED是矩形,
∴DE=OC=3.
【解析】此题主要考查了菱形的性质,以及矩形的判定,关键是掌握矩形的判定定理,以及菱形的性质.
(1)首先证明四边形OCED是平行四边形,再根据菱形的性质可得AC⊥BD,进而得到四边形OCED是矩形;
(2)首先根据菱形的性质可得OD=12BD=4,OC=OA,AD=CD,然后再根据勾股定理可计算出DE=OC=3.
23.【答案】解:(1)如图1,点F即为所求作;
(2)如图2,菱形EFGH即为所求作.
【解析】本题考查作图−复杂作图,平行四边形的性质,菱形的判定和性质等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
(1)连接AC,BD交于点O,连接OE,延长EO交CD于点F,点F即为所求作;
(2)在线段DC上截取线段DG,使得DG=BE,连接EG,作线段EG的垂直平分线交AD于H,交BC于F,连接EH,GH,EF,FG即可.
24.【答案】6
【解析】(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,
∵AG⊥BD,CH⊥BD,
∴∠AGD=∠CHB=90°,
∵E,F分别为AD,BC的中点,
∴GE=DE=12AD,HF=BF=12BC,
∴EG=HF,∠EDG=∠EGD,∠FBH=∠BHF,
∵AD//BC,
∴∠EDG=∠FBH,
∴∠EGD=∠FHB,
∴EG//FH,
∴四边形GEHF是平行四边形;
(2)解:当BD=6时,▱GEHF是矩形,
理由:连接EF交GH于O,
∵四边形ABCD是平行四边形,
∴AD=BC,AD//BC,
∵E,F分别为AD,BC的中点,
∴AE=BF,
∴四边形ABFE是平行四边形,
∴EF=AB=2,
∵AG⊥BD,
∴AB2−BG2=AD2−DG2,
∴22−BG2=32−(6−BG)2,
∴BG=2,
同理可得DH=2,
∴HG=2,
∴EF=HG,
∵四边形GEHF是平行四边形,
∴▱GEHF是矩形,
故答案为:6.
(1)根据平行四边形性质得到AD=BC,根据直角三角形的性质得到GE=DE=12AD,HF=BF=12BC,证得EG//FH,根据平行四边形的判定定理即可得到结论;
(2)连接EF交GH于O,根据平行四边形的性质得到AD=BC,AD//BC,求得EF=AB=2,根据勾股定理和进行的判定定理即可得到结论.
本题考查了矩形的判定,平行四边形的性质和判定,直角三角形的性质,正确地作出辅助线是解题的关键.
25.【答案】(1)证明:∵四边形ABCD是矩形,
∴AD//BC,
∴∠APB=∠PAF,
由翻折的性质得:∠APB=∠APF,
∴∠APF=∠PAF,
∴AF=PF;
(2)解:∵四边形ABCD是矩形,
∴∠B=∠BAD=90°,
①当点E在矩形ABCD内部时,过点E作HG//AB,分别交AD、BC于H、G,延长PE交AD于F,如图③所示:
则HG⊥AD,EH=3,
由翻折的性质得:AE=AB=6,
在Rt△AHE中,EH=12AE,
∴∠EAH=30°,
∴∠BAE=90°−∠EAH=90°−30°=60°,
由折叠的性质得:∠EAP=∠BAP,
∴∠EAP=∠BAP=12∠BAE=12×60°=30°,
∴AP=2BP,
在Rt△ABP中,由勾股定理得:AB2+BP2=AP2,
即62+BP2=(2BP)2,
解得:BP=2 3(负值已舍去);
②当点E在矩形ABCD外部时,过点E作EH//AB,分别交AD于H,如图④所示:
则EH⊥AD,EH=3,
由翻折的性质得:AE=AB=6,
在Rt△AHE中,EH=12AE,
∴∠EAH=30°,
∴∠BAE=90°+∠EAH=90°+30°=120°,
由折叠的性质得:∠EAP=∠BAP,
∴∠EAP=∠BAP=12∠BAE=12×120°=60°,
∴∠APB=90°−60°=30°,
∴AP=2AB=12,
在Rt△ABP中,由勾股定理得:AB2+BP2=AP2,
即62+BP2=122,
解得:BP=6 3(负值已舍去);
综上所述,BP的长为2 3或6 3;
(3)4.8.
【解析】(1)见答案;
(2)见答案;
(3)解:∵四边形ABCD是矩形,
∴AD//BC,AB=CD=6,AD=BC=10,∠ADC=90°,
∴∠DAC=∠BCA,
当点P、E、D在同一直线上时,点P开始向点C运动,开始点F沿DA方向移动,点E与点F重合后,点F又沿AD方向移动,如图②所示:
则点F运动的路程为:DF′+F′F″,
E′与F′重合时,由折叠的性质得:AF′=AB=6,
∴DF′=AD−AF′=10−6=4,
由折叠的性质得:∠BCA=∠E″CA,
∴∠DAC=∠E″CA,
∴AF″=CF″=AD−DF″=10−DF″,
在Rt△CDF″中,由勾股定理得:DF′′2+CD2=CF″2,
即DF″2+62=(10−DF″)2,
解得:DF″=3.2,
∴F′F″=DF′−DF″=4−3.2=0.8,
∴DF′+F′F″=4+0.8=4.8,
故答案为:4.8.
本题是四边形综合题,考查了矩形的性质、平行线的性质、等腰三角形的判定与性质、折叠的性质、勾股定理、含30°角直角三角形的性质、分类讨论等知识;熟练掌握矩形的性质与折叠的性质是解题的关键.种子粒数
100
400
800
1000
2000
5000
发芽种子粒数
85
318
652
793
1604
4005
发芽频率
0.850
0.795
0.815
0.793
0.802
0.801
成绩(单位:分)
频数
频率
A类(80~100)
12
0.3
B类(60~79)
m
0.4
C类(40~59)
8
n
D类(0~39)
4
0.1
相关试卷
这是一份2023-2024学年江苏省南京市秦淮区钟英中学八年级(下)月考数学试卷(3月份)(含解析),共36页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份2022-2023学年江苏省南京市秦淮区第一中学八年级(下)期中数学试卷(含解析),共20页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份2023-2024学年江苏省南京市秦淮区钟英中学八年级(下)3月月考数学试卷(含解析),共31页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。









