2023-2024学年江苏省盐城市滨海县滨淮教育集团七年级（下）月考数学试卷（3月份）（含解析）

这是一份2023-2024学年江苏省盐城市滨海县滨淮教育集团七年级（下）月考数学试卷（3月份）（含解析），共17页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1.如图所示的图案分别是一些汽车的车标，其中，可以看作由“基本图案”经过平移得到的是( )
A. B.
C. D.
2.计算3x2⋅5x5的结果是( )
A. 15x3B. 15x5C. 15x7D. 15x10
3.下列运算不正确的是( )
A. x3+x3=x6B. [(−x)4]3=x12C. x2⋅x3=x5D. (−x3)4=x12
4.下列长度的三根木棒首尾相接，不能做成三角形框架的是( )
A. 5cm、7cm、2cmB. 7cm、13cm、10cm
C. 5cm、7cm、11cmD. 5cm、10cm、13cm
5.一个多边形的内角和为1080°，它为边形．( )
A. 10B. 6C. 8D. 12
6.如图所示，直线m/​/n，若∠1=63°，∠2=40°.则∠BAC的度数是( )
A. 67°
B. 77°
C. 97°
D. 103°
7.小明同学在计算某n边形的内角和时，不小心少输入一个内角，得到和为2000°，则n等于( )
A. 11B. 12C. 13D. 14
8.如图，将△ABC纸片沿DE折叠使点A落在点A′处，且BA′平分∠ABC，CA′平分∠ACB，若∠BA′C=112°，则∠1+∠2的大小为( )
A. 44°
B. 41°
C. 88°
D. 82°
二、填空题：本题共8小题，每小题3分，共24分。
9.(−0.25)2007×42007= ______．
10.已知ax=3，ay=2，则a2x+3y= ______．
11.已知一个n边形的每一个外角都为30°，则n等于______．
12.已知一个等腰三角形的两边边长为3和4，则这个等腰三角形的周长为______．
13.如图，直线a、b被直线c所截，∠2=65°，当∠1=______°时，a/​/b．
14.如图，将周长为8的△ABC沿BC方向向右平移1个单位得到△DEF，则四边形ABFD的周长为 ．
15.如图，△ABC的面积是4，点D、E、F分别是BC、AD、BE的中点，则△CEF的面积是______．
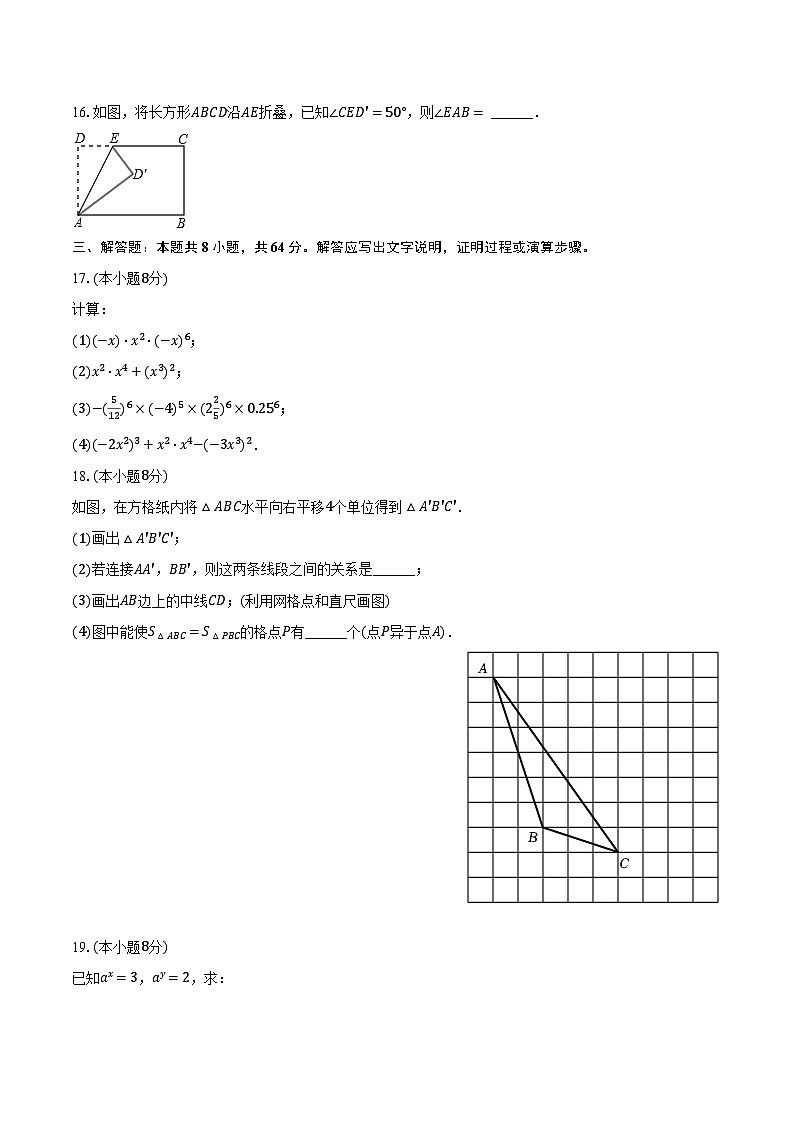
16.如图，将长方形ABCD沿AE折叠，已知∠CED′=50°，则∠EAB= ______．
三、解答题：本题共8小题，共64分。解答应写出文字说明，证明过程或演算步骤。
17.(本小题8分)
计算：
(1)(−x)⋅x2⋅(−x)6；
(2)x2⋅x4+(x3)2；
(3)−(512)6×(−4)5×(225)6×0.256；
(4)(−2x2)3+x2⋅x4−(−3x3)2．
18.(本小题8分)
如图，在方格纸内将△ABC水平向右平移4个单位得到△A′B′C′．
(1)画出△A′B′C′；
(2)若连接AA′，BB′，则这两条线段之间的关系是______；
(3)画出AB边上的中线CD；(利用网格点和直尺画图)
(4)图中能使S△ABC=S△PBC的格点P有______个(点P异于点A)．
19.(本小题8分)
已知ax=3，ay=2，求：
①ax+y的值；
②a3x+2y的值．
20.(本小题8分)
(1)已知3×9m×27m=98，求m的值；
(2)已知2x+5y+4=0，求4x×32y的值．
21.(本小题8分)
如图，在△ABC中，点D、E分别在AB、BC上，且DE/​/AC，∠1=∠2．
(1)求证：AF/​/BC．
(2)若AC平分∠BAF，∠B=50°，求∠1的度数．
22.(本小题8分)
如图，在△ABC中，CD为△ABC的高，AE为△ABC的角平分线，CD交AE于点G，∠BCD=50°，∠BEA=110°，求∠ACD的度数．
23.(本小题8分)
如图，在△ABC中，AD⊥BC，AE平分∠BAC，∠1=30°，∠2=20°，则∠B= ______度.
24.(本小题8分)
【数学经验】三角形的中线，角平分线，高是三角形的重要线段，我们知道，三角形的3条高所在直线交于同一点．
(1)①如图1，△ABC中，∠A=90°，则△ABC的三条高所在的直线交于点______；
②如图2，△ABC中，∠BAC>90°，已知两条高BE，AD，请你仅用一把无刻度的直尺(仅用于过任意两点作直线、连接任意两点、延长任意线段)画出△ABC的第三条高．(不写画法，保留作图痕迹)．
【综合应用】
(2)如图3，在△ABC中，∠ABC>∠C，AD平分∠BAC，过点B作BE⊥AD于点E．
①若∠ABC=80°，∠C=30°，则∠EBD=______°；
②请写出∠EBD与∠ABC，∠C之间的数量关系______，并说明理由．
【拓展延伸】
(3)三角形的中线将三角形分成面积相等的两部分，如果两个三角形的高相同，则它们的面积比等于对应底边的比．如图4，M是BC上一点，则有S△ABMS△ACM=BMCM．
如图5，△ABC中，M是BC上一点BM=14BC，N是AC的中点，若三角形ABC的面积是m，求四边形CMDN的面积．(用含m的代数式表示)
答案和解析
1.【答案】D
【解析】解：A、可以由一个“基本图案”旋转得到，不可以由一个“基本图案”平移得到，故本选项错误；
B、是轴对称图形，不是基本图案的组合图形，故本选项错误
C、不可以由一个“基本图案”平移得到，故把本选项错误；
D、可以由一个“基本图案”平移得到，故把本选项正确；
故选：D．
根据旋转变换，平移变换，轴对称变换对各选项分析判断后利用排除法求解．
本题考查了生活中的平移现象，仔细观察各选项图形是解题的关键．
2.【答案】C
【解析】解：3x2⋅5x5=15x7，
故选：C．
根据单项式乘单项式的运算法则计算即可．
本题考查的是单项式乘单项式，单项式与单项式相乘，把他们的系数，相同字母分别相乘，对于只在一个单项式里含有的字母，则连同它的指数作为积的一个因式．
3.【答案】A
【解析】解：A.∵x3+x3=2x3，∴此选项的计算错误，故此选项符合题意；
B.∵[(−x)4]3=(−x)12=x12，∴此选项的计算正确，故此选项不符合题意；
C.∵x2⋅x3=x5，∴此选项的计算正确，故此选项不符合题意；
D.∵(−x3)4=x12，∴此选项的计算正确，故此选项不符合题意；
故选：A．
A.利用合并同类项法则进行合并，然后判断即可；
B.D选项根据幂的乘方法则进行计算，然后判断即可；
C.根据同底数幂相乘法则进行计算，然后判断即可．
本题主要考查了整式的有关运算，解题关键是熟练掌握幂的乘方法则、同底数幂相乘法则和合并同类项法则．
4.【答案】A
【解析】解：A中，5+2=7，不能组成三角形；
B中，10+7>13，10−7<13，能组成三角形；
C中，5+7>11，7−5<11，能组成三角形；
D中，5+10>13，10−5<13，能组成三角形，
故选：A．
根据三角形的三边关系“两边之和大于第三边，两边之差小于第三边”进行分析判断．
本题考查了三角形的三边关系，一定注意构成三角形的三边关系：两边之和大于第三边，两边之差小于第三边．
5.【答案】C
【解析】解：设多边形是n边形，由内角和公式，
得(n−2)×180°=1080°．
解得n=8，
故选：C．
根据多边形的内角和公式，可得方程，解方程，可得答案．
本题考查了多边形的内角与外角，利用了多边形的内角和公式是解题根据．
6.【答案】B
【解析】解：如图：
∵直线m/​/n，∠2=40°．
∴∠3=∠2=40°．
∵∠1+∠BAC+∠3=180°，∠1=63°，
∴∠BAC=180°−63°−40°=77°．
故选：B．
由直线m/​/n，利用“两直线平行，内错角相等”可求出∠3的度数，再结合∠1+∠BAC+∠3=180°，即可求出∠BAC的度数．
本题考查了平行线的性质，利用“两直线平行，内错角相等”求出∠3的度数是解题的关键．
7.【答案】D
【解析】解：设少输入的内角度数为α，
由题意得，(n−2)⋅180°=2000°+α，
解得n=14，α=160°．
故选：D．
设少输入的内角度数为α，然后根据多边形的内角和公式(n−2)⋅180°列方程求解即可．
本题考查了多边形内角与外角，解题的关键在于明确多边形的内角和是180°的整数倍．
8.【答案】C
【解析】解：如图，连接AA′．
∵∠BA′C=112°，
∴∠A′BC+∠A′CB=180°−∠BA′C=68°．
∵BA′平分∠ABC，CA′平分∠ACB，
∴∠ABC=2∠A′BC，∠ACB=2∠A′CB．
∴∠ABC+∠ACB=2∠A′BC+2∠A′CB=2(∠A′BC+∠A′CB)=136°．
∴∠BAC=180°−(∠ABC+∠ACB)=44°．
由题意得：△ADE≌△A′DE．
∴∠DAE=∠DA′E=44°．
∵∠1=∠DAA′+∠AA′D，∠2=∠EAA′+∠AA′E，
∴∠1+∠2=∠DAA′+∠EAA′+∠DA′A+∠EA′A=∠DAE+∠DA′E=2∠DAE=88°．
故选：C．
由题意得△ADE≌△A′DE，那么∠DAE=∠DA′E.如图，连接AA′.根据三角形外角的性质，得∠1=∠DAA′+∠AA′D，∠2=∠EAA′+∠AA′E，那么∠1+∠2=∠DAE+∠DA′E=2∠DAE.欲求∠1+∠2，需求∠DAE.由三角形内角和定理得∠DAE=180°−∠ABC−∠ACB.由BA′平分∠ABC，CA′平分∠ACB，得∠ABC=2∠A′BC，∠ACB=2∠A′CB，那么∠ABC+∠ACB=2∠A′BC+2∠A′CB=2(∠A′BC+∠A′CB).由∠BA′C=112°，得∠A′BC+∠A′CB=180°−∠BA′C=68°，从而解决此题．
本题主要考查三角形内角和定理、角平分线的定义、图形折叠的性质，三角形外角的性质，熟练掌握三角形内角和定理、角平分线的定义、图形折叠的性质，三角形外角的性质是解决本题的关键．
9.【答案】−1
【解析】解：(−0.25)2007×42007
=(−0.25×4)2007
=(−1)2007
=−1．
故答案为：−1．
利用积的乘方的法则进行运算即可．
本题主要考查积的乘方，解答的关键是对相应的运算法则的掌握．
10.【答案】72
【解析】解：∵ax=3，ay=2，
∴a2x+3y
=a2x⋅a3y
=(ax)2⋅(ay)3
=32⋅23
=72．
故答案为：72．
利用同底数幂的乘法和幂的乘方运算法则将a2x+3y整理，再将已知条件代入计算即可．
本题考查幂的乘方与积的乘方、同底数幂的乘法，掌握其运算法则是解题的关键．
11.【答案】12
【解析】【分析】
本题主要考查多边形的外角和定理，解答本题的关键是掌握任意多边形的外角和都是360°．
根据多边形的外角和等于360°列式计算即可．
【解答】
解：∵一个n边形的每一个外角都为30°，任意多边形的外角和都是360°，
∴n=360°÷30°=12．
故答案为12．
12.【答案】10或11
【解析】解：等腰三角形的腰长为3，底为4时，能构成三角形，这个等腰三角形的周长为：3+3+4=10，
等腰三角形的腰长为4时，底为3时，能构成三角形，这个等腰三角形的周长为：3+4+4=11，
故答案为：10或11．
由于未说明两边哪个是腰，故分情况讨论．
此题考查了等腰三角形的性质、三角形三边关系，熟记等腰三角形的性质是解题的关键．
13.【答案】115
【解析】解：如图，当a/​/b时，∠3=∠2=65°，
∴∠1=180°−∠3=115°，
故答案为：115．
依据平行线的性质，即可得到∠3的度数，进而得出∠1的度数．
本题考查了平行线的性质．解题时注意：同位角相等，两直线平行．
14.【答案】10
【解析】解：根据题意，将周长为8的△ABC沿边BC向右平移1个单位得到△DEF，
则AD=1，BF=BC+CF=BC+1，DF=AC，
又∵AB+BC+AC=8，
∴四边形ABFD的周长=AD+AB+BF+DF=1+AB+BC+1+AC=10．
故答案为：10．
根据平移的基本性质解答即可．
本题考查平移的基本性质：①平移不改变图形的形状和大小；②经过平移，对应点所连的线段平行(或共线)且相等，对应线段平行(或共线)且相等，对应角相等．得到CF=AD，DF=AC是解题的关键．
15.【答案】1
【解析】解：∵S△ABC=4，点E是AD的中点，
∴S△BCE=12S△ABC=12×4=2，
又∵点F是BE的中点，
∴S△CEF=12S△BCE=12×2=1．
故答案为：1．
首先根据S△ABC=4，点E是AD的中点，判断出S△BCE=12S△ABC；然后根据点E是AD的中点，求出S△CEF是多少即可．
此题主要考查了三角形的面积的求法，要熟练掌握．
16.【答案】65°
【解析】解：∵∠CED′=50°，
∴∠D′ED=180°−50°=130°，
∵将长方形ABCD沿AE折叠D和D′重合，
∴∠D=∠D′=90°，∠DAE=∠D′AE，
∴∠DAD′=360°−90°−90°−130°=50°，
∴∠DAE=∠D′AE=25°，
∵∠DAB=90°，
∴∠EAB=90°−25°=65°，
故答案为：65°．
求出∠DED′，根据多边形的内角和定理求出∠DAD′，根据折叠求出∠DAE，即可求出答案．
本题考查了长方形的性质和折叠的性质的应用，解此题的关键是求出∠DAE的度数，题目比较好，难度适中．
17.【答案】解：(1)(−x)⋅x2⋅(−x)6
=−x⋅x2⋅x6
=−x9；
(2)x2⋅x4+(x3)2
=x2⋅x4+x6
=x6+x6
=2x6；
(3)−(512)6×(−4)5×(225)6×0.256
=(512)6×45×(125)6×(14)6
=(512×125)6×14×(4×14)5
=14；
(4)(−2x2)3+x2⋅x4−(−3x3)2
=−8x6+x6−9x6
=−16x6．
【解析】(1)利用同底数幂的乘法运算法则计算即可；
(2)利用同底数幂的乘法、幂的乘方运算法则计算即可；
(3)利用幂和乘方运算法则计算即可；
(4)利用积的乘方、幂的乘方、同底数幂的乘法运算法则计算即可．
本题考查积的乘方、幂的乘方、同底数幂的乘法，掌握它们的运算法则是本题的关键．
18.【答案】平行且相等 3
【解析】解：(1)如图，△A′B′C′即为所求．
(2)由平移可得，AA′=BB′，且AA′/​/BB′．
故答案为：平行且相等．
(3)如图，CD即为所求．
(4)如图，过点A作BC的平行线，所经过的格点P1，P2，P3即为满足条件的点P，共有3个．
故答案为：3．
(1)根据平移的性质作图即可．
(2)由平移可知，AA′=BB′，且AA′/​/BB′．
(3)利用网格取AB的中点D，连接CD即可．
(4)利用网格，过点A作BC的平行线，所经过的格点即为满足条件的点P，从而可得答案．
本题考查作图−平移变换、三角形的中线、平行线的性质，熟练掌握平移的性质以及平行线的性质是解答本题的关键．
19.【答案】解：①∵ax=3，ay=2，
∴ax+y=ax⋅ay
=3×2
=6；
②∵ax=3，ay=2，
∴a3x+2y=a3x⋅a2y
=(ax)3⋅(ay)2
=33×22
=27×4
=108．
【解析】①运用同底数幂乘法运算即可得到ax+y的值；
②运用同底数幂乘法和幂的乘方运算即可得到a3x+2y的值．
本题主要考查了同底数幂乘法和幂的乘方，正确掌握相关的运算法则是解题的关键．
20.【答案】解：(1)∵3×9m×27m=98，
∴3×32m×33m=316，
即31+5m=316，
∴1+5m=16．
解得：m=3；
(2)∵2x+5y+4=0，
∴2x+5y=−4，
∴4x×32y=22x×25y=22x+5y=2−4=116．
【解析】(1)利用“同底数幂乘法”、“幂的乘方”分别将等式的左右两边化简成底数为3的指数幂形式，得出m的方程，即可求得m的值；
(2)将4x×32y变形为底数为2的指数幂形式，再结合已知条件即可求解．
本题考查了同底数幂乘法、幂的乘方等运算，掌握将指数幂化为相同的底数是关键．
21.【答案】(1)证明：∵DE/​/AC，
∴∠1=∠C，
∵∠1=∠2，
∴∠C=∠2，
∴AF/​/BC；
(2)解：∵AF/​/BC，
∴∠B+∠BAF=180°，
∵∠B=50°，
∴∠BAF=130°，
∵AC平分∠BAF，
∴∠2=12∠BAF=65°，
∵∠1=∠2，
∴∠1=65°．
【解析】(1)根据平行线的性质得出∠1=∠C，求出∠C=∠2，根据平行线的判定得出即可；
(2)根据平行线的性质得出∠B+∠BAF=180°，求出∠BAF=130°，根据角平分线的定义求出∠2=12∠BAF=65°即可．
本题考查了平行线的性质和判定，角平分线的定义等知识点，能灵活运用平行线的性质和判定定理进行推理是解题的关键．
22.【答案】解：∵CD是△ABC的高，
∴∠ADC=∠CDB=90°．
∵∠BCD=50°，
∴∠B=90°−∠BCD=40°．
∵AE平分∠BAC，∠BAE=180°−∠B−∠AEB=180°−40°−110°=30°，
∴∠DAC=2∠BAE=60°，
∴∠ACD=90°−∠DAC=30°．
【解析】本题考查三角形内角和定理，角平分线的定义等知识，解题的关键是利用三角形内角和定理解决问题．
利用三角形内角和定理求出∠BAE，再根据角平分线的定义求出∠DAC，可得结论．
23.【答案】50
【解析】解：∵AE平分∠BAC，∠1=∠EAC，
∴∠1=∠EAD+∠2，
∴∠1−∠2=EAD=30°，
∴∠EAD=∠1−∠2=30°−20°=10°，
∴Rt△ABD中，∠B=90°−∠BAD=90°−30°−10°=50°．
故答案为：50．
由AE平分∠BAC，可得∠BAE和∠EAC相等，由∠1=30°，∠2=20°，可求得∠EAD的度数．已知∠1和∠EAD，在直角三角形ABD中利用两锐角互余，可求得答案．
本题考查了三角形的角平分线、中线和高的相关知识，观察图形可知在直角三角形ABD中，若能求得∠EAD，则可利用内角和求出∠B．
24.【答案】A 25 2∠EBD=∠ABC−∠ACB
【解析】解：(1)①∵直角三角形三条高的交点为直角顶点，∠A=90°，
∴△ABC的三条高所在直线交于点A，
故答案为：A；
②如图2，延长BE、DA交于点F，连接CF，延长BA交CF于点G，则CG为△ABC的第三条高；
(2)①∵∠ABC=80°，∠ACB=30°，
∴∠BAC=70°，
∵AD平分∠BAC，
∴∠BAE=12∠BAC=35°，
∵BE⊥AD，
∴∠AEB=90°，
∴∠ABE=90°−35°=55°，
∴∠EBD=∠ABC−∠ABE=80°−55°=25°，
故答案为：25°；
②∠EBD与∠ABC，∠C之间的数量关系为：2∠EBD=∠ABC−∠ACB，理由如下：
∵BE⊥AD，
∴∠AEB=90°，
∴∠ABE=90°−∠BAD，
∴∠EBD=∠ABC−∠ABE=∠ABC+∠BAD−90°，
∵AD平分∠BAC，
∴∠BAD=∠CAD=12∠BAC，
∵∠BAC=180°−∠ABC−∠ACB，
∴∠BAD=90°−12∠ABC−12∠ACB，
∴∠EBD=∠ABC+∠BAD−90°=∠ABC+90°−12∠ABC−12∠C−90°=12∠ABC−12∠ACB，
∴2∠EBD=∠ABC−∠ACB，
故答案为：2∠EBD=∠ABC−∠ACB；
(3)连接CD，如图5所示：
∵N是AC的中点，
∴S△ADNS△CDN=ANCN=1，
∴S△ADN=S△CDN，
同理：S△ABN=S△CBN，
设S△ADN=S△CDN=a，
∵△ABC的面积是m，
∴S△ABN=S△CBN=12m，
∴S△BCD=S△ABD=12m−a，
∵BM=14BC，
∴BMCM=13，
∴S△BDMS△CDM=BMCM=13，S△ABMS△ACM=BMCM=13，
∴S△CDM=3S△BDM，S△ACM=3S△ABM，
∴S△CDM=34S△BCD=34×(12m−a)=38m−34a，S△ACM=34S△ABC=34m，
∵S△ACM=S四边形CMDN+S△ADN=S△CDM+S△CDN+S△ADN，
即：34m=38m−34a+a+a，
解得：a=310m，
∴S四边形CMDN=S△CDM+S△CDN=38m−34×310m+310m=1320m.
(1)①由直角三角形三条高的定义即可得出结论；
②延长BE、DA交于点F，连接CF，延长BA交CF于点G，则CG为△ABC的第三条高；
(2)①由三角形内角和定理和角平分线定义得∠BAE=12∠BAC=35°，再由直角三角形的性质得∠ABE=55°，即可求解；
②由三角形内角和定理和角平分线定义求解即可；
(3)连接CD，由中线的性质得S△ADN=S△CDN，同理S△ABN=S△CBN，设S△ADN=S△CDN=a，则S△ABN=S△CBN=12m，再求出S△CDM=34S△DBC=38m−34a，S△ACM=34S△ABC=34m，然后由面积关系求出a=310m，即可解决问题．
本题是四边形综合题目，考查了四边形面积的计算、三角形的高、三角形的中线、三角形内角和定理、三角形的面积等知识；本题综合性强，熟练掌握三角形的三条高交于一点和三角形面积关系是解题的关键．