


还剩20页未读,
继续阅读
初中数学人教版九年级上册23.1 图形的旋转课文内容ppt课件
展开
这是一份初中数学人教版九年级上册23.1 图形的旋转课文内容ppt课件,共28页。PPT课件主要包含了确定点E的对应点E,旋转中心,旋转角,教材P62练习等内容,欢迎下载使用。
复习旋转及旋转图形的概念及基本性质,了解旋转作图的步骤和关键.掌握简单平面图形旋转的作法,能按要求作出简单平面图形旋转后的图形.体会旋转在图形变换中的作用,能利用旋转进行简单的图案设计.
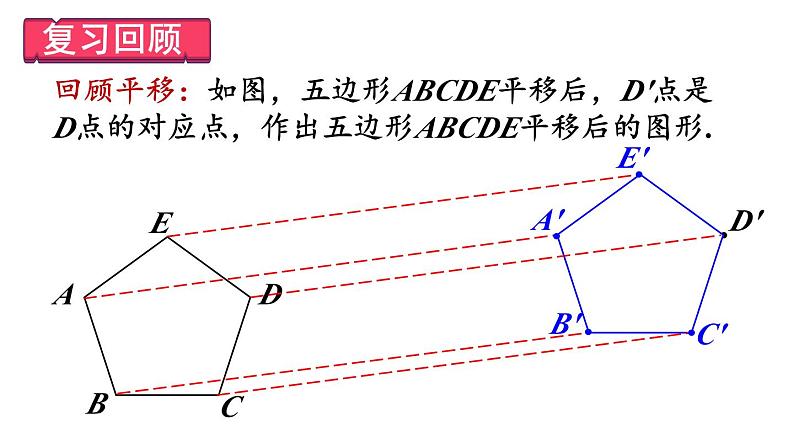
回顾平移:如图,五边形ABCDE平移后,D'点是D点的对应点,作出五边形ABCDE平移后的图形.
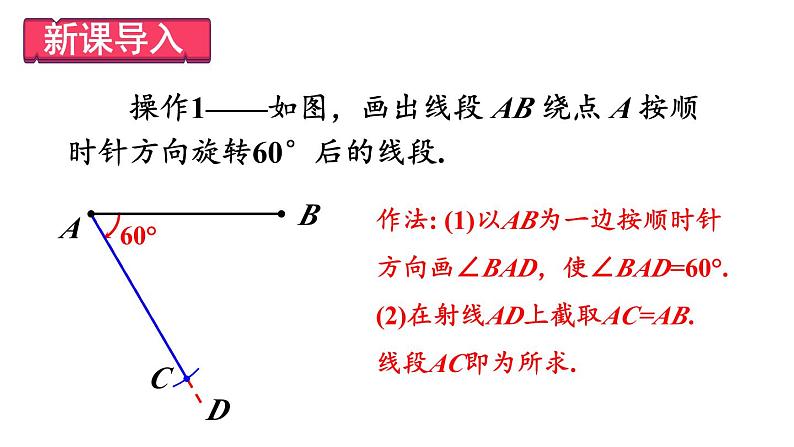
操作1——如图,画出线段 AB 绕点 A 按顺时针方向旋转60°后的线段.
作法: (1)以AB为一边按顺时针方向画∠BAD,使∠BAD=60°.(2)在射线AD上截取AC=AB. 线段AC即为所求.
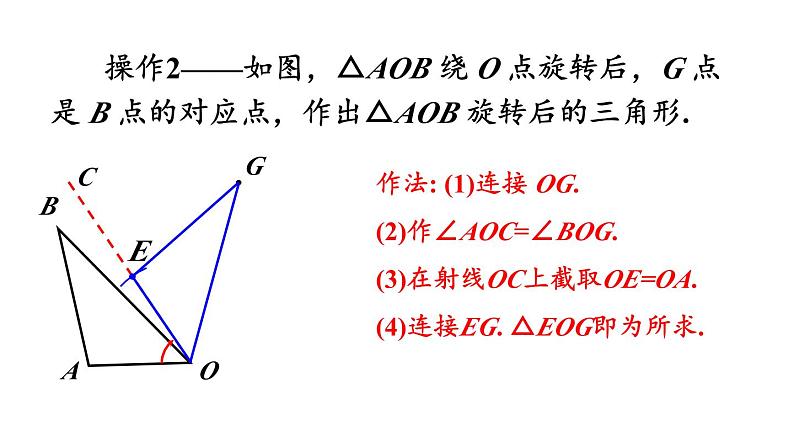
操作2——如图,△AOB 绕 O 点旋转后,G 点是 B 点的对应点,作出△AOB 旋转后的三角形.
作法: (1)连接 OG.(2)作∠AOC=∠BOG.(3)在射线OC上截取OE=OA.(4)连接EG. △EOG即为所求.
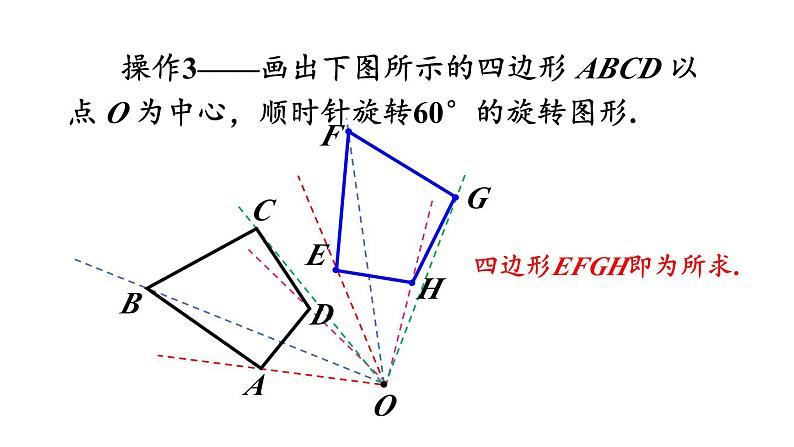
操作3——画出下图所示的四边形 ABCD 以点 O 为中心,顺时针旋转60°的旋转图形.
四边形EFGH即为所求.
你能总结出旋转作图的一般步骤吗?
举例:画出旋转后的三角形.
例 如图,E是正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形.
A DB C
解:因为点A是旋转中心,所以它的对应点是 .正方形ABCD中,AD=AB,∠DAB=90°,所以旋转后点D与点 重合.
设点E的对应点为点E'. 因为旋转后的图形与旋转前的图形全等,所以∠ABE'=∠ADE=90°,BE'=DE.因此,在CB的延长线上取点E',使BE'=DE,则△ABE'为旋转后的图形.
E点的对应点E′,还可以用其他方法确定吗?
方法一:由∠EAE′=90°,AE′=AE确定点E′.
方法二:由∠ABE′=90°,AE′ =AE可知,以点A为圆心,AE为半径画弧,和CB的延长线的交点即是点E′.
方法三:由∠ABE′=90°,∠EAE’=90°可知,过点A作AE垂直的直线与CB的延长线的交点即是E′.
任意画一个△ABC,以点A为旋转中心,把这个三角形逆时针旋转40°;
任意画一个△ABC,以AC中点为旋转中心,把这个三角形旋转180°.
选择不同的__________、不同的________旋转同一个图案,会出现不同的效果.
旋转中心不变,旋转角改变
旋转角不变,旋转中心改变
你还能通过旋转 设计出其他不同的图案吗?
我们可以借助旋转设计出许多美丽的图案.
把一个三角形进行旋转:(1)选择不同的旋转中心、不同的旋转角,看看旋转的效果;(2)改变三角形的形状,看看旋转的效果.
旋转角不变,改变旋转中心(答案不唯一)
旋转中心、旋转角都改变(答案不唯一)
1. 下面的图形是由一个基本的图形经过旋转得到的,分别指出它们的旋转中心和旋转角.
【教材P63习题23.1 第5题】
2. △ABC中,AB=AC,P 是 BC 边上任意一点. 以点 A 为中心,取旋转角等于∠BAC,把△ABP逆时针旋转,画出旋转后的图形.
【教材P62习题23.1 第3题】
解:如图所示,△ACP'即为所求作的图形.
3. 分别画出△ABC绕点O逆时针旋转90°和180°后的图形.
【教材P62习题23.1 第4题】
解:旋转90°后的图形如图所示.
旋转180°后的图形如图所示.
4. 如图,△ABC中,∠C=90°.(1)将△ABC绕点B逆时针旋转90°,画出旋转后的三角形;(2)若BC=3,AC=4,点A旋转后的对应点为A,求A'A的长.
【教材P63习题23.1 第9题】
解:(1)△A'BC'即为所求.
(2)∵△ABC中,∠C=90°,BC=3,AC=4.∴AB= =5. 由旋转的性质可得△A'BA 中,∠A'BA =90°,A'B=AB=5.∴A'A= .
5. 以原点为中心,把点A(4,5)逆时针旋转90°,得到点B. 求点B的坐标.
【教材P63习题23.1 第11题】
解:如图所示,画出旋转后的边OB.过点A作AC⊥x轴于点C.∵点A坐标为(4,5),∴在Rt△ACO中,AC=5,OC=4.由题意知,△ACO绕点O逆时针旋转90°得到△BC'O,∴BC'=AC=5,OC'=OC=4.∵点B在第二象限,∴点B的坐标为(-5,4).
复习旋转及旋转图形的概念及基本性质,了解旋转作图的步骤和关键.掌握简单平面图形旋转的作法,能按要求作出简单平面图形旋转后的图形.体会旋转在图形变换中的作用,能利用旋转进行简单的图案设计.
回顾平移:如图,五边形ABCDE平移后,D'点是D点的对应点,作出五边形ABCDE平移后的图形.
操作1——如图,画出线段 AB 绕点 A 按顺时针方向旋转60°后的线段.
作法: (1)以AB为一边按顺时针方向画∠BAD,使∠BAD=60°.(2)在射线AD上截取AC=AB. 线段AC即为所求.
操作2——如图,△AOB 绕 O 点旋转后,G 点是 B 点的对应点,作出△AOB 旋转后的三角形.
作法: (1)连接 OG.(2)作∠AOC=∠BOG.(3)在射线OC上截取OE=OA.(4)连接EG. △EOG即为所求.
操作3——画出下图所示的四边形 ABCD 以点 O 为中心,顺时针旋转60°的旋转图形.
四边形EFGH即为所求.
你能总结出旋转作图的一般步骤吗?
举例:画出旋转后的三角形.
例 如图,E是正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形.
A DB C
解:因为点A是旋转中心,所以它的对应点是 .正方形ABCD中,AD=AB,∠DAB=90°,所以旋转后点D与点 重合.
设点E的对应点为点E'. 因为旋转后的图形与旋转前的图形全等,所以∠ABE'=∠ADE=90°,BE'=DE.因此,在CB的延长线上取点E',使BE'=DE,则△ABE'为旋转后的图形.
E点的对应点E′,还可以用其他方法确定吗?
方法一:由∠EAE′=90°,AE′=AE确定点E′.
方法二:由∠ABE′=90°,AE′ =AE可知,以点A为圆心,AE为半径画弧,和CB的延长线的交点即是点E′.
方法三:由∠ABE′=90°,∠EAE’=90°可知,过点A作AE垂直的直线与CB的延长线的交点即是E′.
任意画一个△ABC,以点A为旋转中心,把这个三角形逆时针旋转40°;
任意画一个△ABC,以AC中点为旋转中心,把这个三角形旋转180°.
选择不同的__________、不同的________旋转同一个图案,会出现不同的效果.
旋转中心不变,旋转角改变
旋转角不变,旋转中心改变
你还能通过旋转 设计出其他不同的图案吗?
我们可以借助旋转设计出许多美丽的图案.
把一个三角形进行旋转:(1)选择不同的旋转中心、不同的旋转角,看看旋转的效果;(2)改变三角形的形状,看看旋转的效果.
旋转角不变,改变旋转中心(答案不唯一)
旋转中心、旋转角都改变(答案不唯一)
1. 下面的图形是由一个基本的图形经过旋转得到的,分别指出它们的旋转中心和旋转角.
【教材P63习题23.1 第5题】
2. △ABC中,AB=AC,P 是 BC 边上任意一点. 以点 A 为中心,取旋转角等于∠BAC,把△ABP逆时针旋转,画出旋转后的图形.
【教材P62习题23.1 第3题】
解:如图所示,△ACP'即为所求作的图形.
3. 分别画出△ABC绕点O逆时针旋转90°和180°后的图形.
【教材P62习题23.1 第4题】
解:旋转90°后的图形如图所示.
旋转180°后的图形如图所示.
4. 如图,△ABC中,∠C=90°.(1)将△ABC绕点B逆时针旋转90°,画出旋转后的三角形;(2)若BC=3,AC=4,点A旋转后的对应点为A,求A'A的长.
【教材P63习题23.1 第9题】
解:(1)△A'BC'即为所求.
(2)∵△ABC中,∠C=90°,BC=3,AC=4.∴AB= =5. 由旋转的性质可得△A'BA 中,∠A'BA =90°,A'B=AB=5.∴A'A= .
5. 以原点为中心,把点A(4,5)逆时针旋转90°,得到点B. 求点B的坐标.
【教材P63习题23.1 第11题】
解:如图所示,画出旋转后的边OB.过点A作AC⊥x轴于点C.∵点A坐标为(4,5),∴在Rt△ACO中,AC=5,OC=4.由题意知,△ACO绕点O逆时针旋转90°得到△BC'O,∴BC'=AC=5,OC'=OC=4.∵点B在第二象限,∴点B的坐标为(-5,4).














