人教A版 (2019)选择性必修 第一册3.2 双曲线授课ppt课件

这是一份人教A版 (2019)选择性必修 第一册3.2 双曲线授课ppt课件，共54页。PPT课件主要包含了F1F2＝2c，x≤－a或x≥a，y≤－a或y≥a，坐标轴，A1A2，B1B2，预习自测，答案B，答案D，微思考等内容，欢迎下载使用。
| 自 学 导 引 |
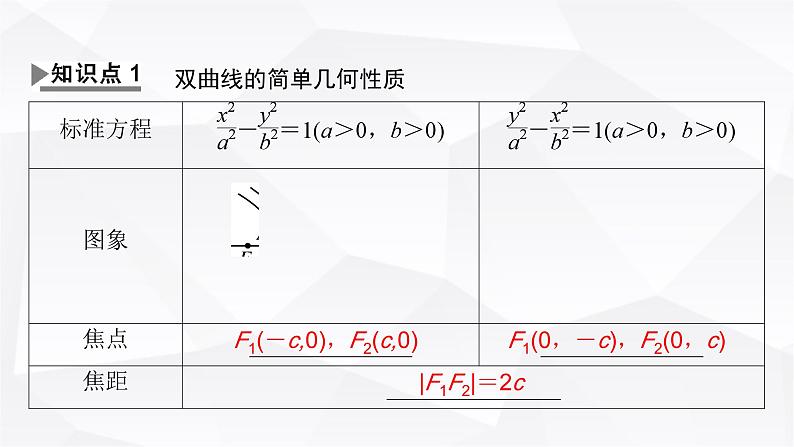
　　　　双曲线的简单几何性质
F1(－c,0)，F2(c,0)　
F1(0，－c)，F2(0，c)　
A1(－a,0)，A2(a,0)
A1(0，－a)，A2(0，a)　
【答案】(1)√　(2)×
若双曲线确定，则渐近线确定吗？反过来呢？
　　　　等轴双曲线实轴和虚轴等长的双曲线，标准方程为______________．
【答案】(1)×　(2)√
2．设双曲线的渐近线方程为y＝±x，则该双曲线的离心率e＝__________．
| 课 堂 互 动 |
【答案】(1)B　(2)C
用双曲线标准方程研究几何性质的步骤(1)将双曲线方程化为标准形式．(2)判断焦点位置．(3)求出a，b，c的值．(4)写出双曲线的几何性质．
【答案】(1)4　(2)y＝±x　
题型2　利用双曲线的几何性质求标准方程
【答案】(1)D　(2)C
由几何性质求双曲线标准方程的解题思路由双曲线的几何性质求双曲线的标准方程，一般用待定系数法．当双曲线的焦点不明确时，方程可能有两种形式，此时应注意分类讨论，为了避免讨论，也可设双曲线的方程为mx2－ny2＝1(mn＞0).
【例题迁移】　(变换条件)本例(2)中条件“若|PF1|＋|PF2|＝6a，且△PF1F2的最小内角为30°”改为“若PF1⊥PF2，且∠PF1F2＝30°”结果如何？
错解分析：错误的根本原因是误以为焦点只能在x轴上，造成失解．实际上本题应该有两种情况．
防范措施：条件考虑要全面由渐近线不能确定焦点是在x轴上，还是在y轴上，因此需要分两种情况讨论．在求解圆锥曲线问题时，既要分析定量条件，又要分析定位条件，以免造成失解、错解．
| 素 养 达 成 |
1．已知双曲线的几何性质确定双曲线的标准方程，常用待定系数法，首先要依据焦点的位置设出方程的形式，再由题设条件确定参数的值；当双曲线焦点位置不确定时，方程可能有两种形式，此时应注意分类讨论，以防止遗漏．
2．(题型2)中心在原点，实轴在x轴上，一个焦点在直线3x－4y＋12＝0上的等轴双曲线方程是(　　)A．x2－y2＝8B．x2－y2＝4C．y2－x2＝8D．y2－x2＝4【答案】A
【答案】C【解析】由已知焦点在x轴上，所以m＞0．所以m＋3m＝4，m＝1．所以双曲线的实轴长为2．