




所属成套资源:苏教版2019必修第二册2023-2024学年高一数学下册期中复习+模拟
- 【期中复习】苏教版2019必修第二册2023-2024学年高一下册数学 专题01 奔驰定理与三角形“四心”(考点专练) 试卷 0 次下载
- 【期中复习】苏教版2019必修第二册2023-2024学年高一下册数学 专题01 平面向量(考点梳理) 试卷 1 次下载
- 【期中复习】苏教版2019必修第二册2023-2024学年高一下册数学 专题02 三角恒等变换(考点梳理) 试卷 0 次下载
- 【期中复习】苏教版2019必修第二册2023-2024学年高一下册数学 专题02 三角恒等变换(考点讲解) 课件 0 次下载
- 【期中复习】苏教版2019必修第二册2023-2024学年高一下册数学 专题02 平面向量最值与范围问题(考点专练) 试卷 1 次下载
【期中复习】苏教版2019必修第二册2023-2024学年高一下册数学 专题01 平面向量(考点讲解)
展开
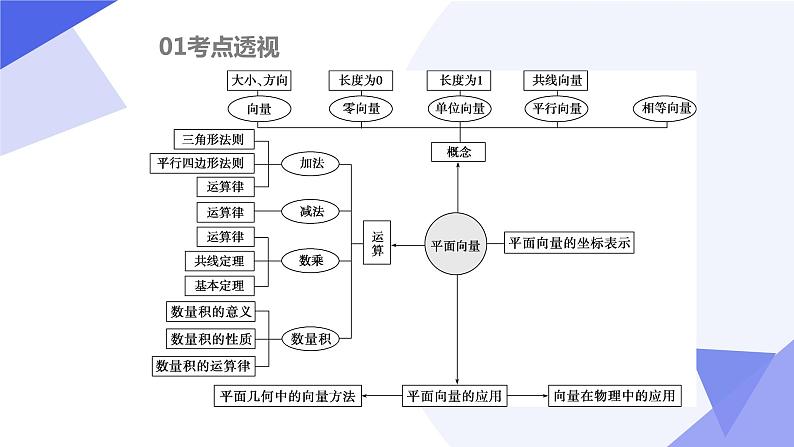
这是一份【期中复习】苏教版2019必修第二册2023-2024学年高一下册数学 专题01 平面向量(考点讲解),共60页。PPT课件主要包含了考场练兵,典例剖析,考点透视,要点二向量的数量积等内容,欢迎下载使用。
要点一 平面向量的线性运算及应用
向量线性运算的基本原则和求解策略(1)基本原则:向量的加法、减法和数乘运算统称为向量的线性运算.向量的线性运算的结果仍是一个向量,因此,对它们的运算法则、运算律的理解和运用要注意向量的大小和方向两个方面.
(2)求解策略:①向量是一个有“形”的几何量,因此在进行向量线性运算时,一定要结合图形,这是研究平面向量的重要方法与技巧.
数量积运算是向量运算的核心,利用向量数量积可以解决以下问题:(1)设a=(x1,y1),b=(x2,y2),则a∥b⇔x1y2-x2y1=0,a⊥b⇔x1x2+y1y2=0.(2)求向量的夹角和模的问题
(2)求a·b的最小值,并求出此时a与b的夹角θ的大小.
又∵0°≤θ≤180°,∴θ=60°.
要点三 平面向量在几何中的应用
把几何图形放到适当的坐标系中,就赋予了有关点与向量具体的坐标,这样就能进行相应的代数运算和向量运算,从而解决问题.这样的解题方法具有普遍性.
解析 由题意,得∠AOC=90°,故以O为坐标原点,OC,OA所在直线分别为x轴、y轴建立平面直角坐标系,如图,
【训练3】 在△ABC中,AB=AC,D为AB的中点,E为△ACD的重心,F为△ABC的外心,证明:EF⊥CD.证明 以BC的中点O为坐标原点,建立如图所示的平面直角坐标系.
设A(0,b),B(-a,0),C(a,0),
易知△ABC的外心F在y轴上,可设为(0,y).
要点四 平面向量在物理中的应用
把物理问题转化为数学问题,建立以向量为主体的数学模型求出数学模型的有关解,然后回到问题的初始状态,解释相关的物理现象,从而得出答案.
【例4】 奥运会帆船比赛是借助风帆推动船只在规定距离内竞速的一项水上运动.如果一帆船所受的风力方向为北偏东30°,速度大小为20 km/h,此时水的流向是正东,流速大小为20 km/h,若不考虑其他因素,求帆船行驶的速度大小与方向.解 如图所示,建立平面直角坐标系(x轴的正方向为东,y轴的正方向为北).风力的方向为北偏东30°,速度大小为|v1|=20 km/h,水流的方向为正东,速度大小为|v2|=20 km/h,帆船行驶的速度为v,则v=v1+v2.
∵α为锐角,∴α=30°.
解 因为F1,F2,F3三个力处于平衡状态,所以F1+F2+F3=0,所以F3=-(F1+F2),
向量线性运算的基本原则向量的加法、减法和数乘运算统称为向量的线性运算,向量的线性运算的结果仍是一个向量,因此,对它们的运算法则、运算律的理解和运用要注意向量的大小和方向两个方面.
向量数量积的两种计算方法(1)当已知向量的模和夹角θ时,可利用定义法求解,即a·b=|a||b|cs θ.(2)当已知向量的坐标时,可利用坐标法求解,即若a=(x1,y1),b=(x2,y2),则a·b=x1x2+y1y2.
【解析】 (1)因为m+n=(2λ+3,3),m-n=(-1,-1),(m+n)⊥(m-n),所以(m+n)·(m-n)=(2λ+3,3)·(-1,-1)=-2λ-6=0,解得λ=-3.
解决两个向量垂直问题,其关键在于将问题转化为它们的数量积为零,与求夹角相似.若向量能用坐标表示(或能建立适当的直角坐标系),将它转化为“x1x2+y1y2=0”则较为简单.
1.设向量a=(1,0),b=(-1,m).若a⊥(ma-b),则m=________. 解析:因为a=(1,0),b=(-1,m),所以ma-b=(m+1,-m).由a⊥(ma-b)得a·(ma-b)=0,即m+1=0,得m=-1.答案:-1
向量应用的求解策略向量的应用主要是指在物理与在平面几何中的应用,首先应将实际问题转化为向量问题解决,然后利用向量的几何意义、向量的运算解决实际问题.
相关课件
这是一份【期中复习】苏教版2019必修第二册2023-2024学年高一下册数学 专题03 解三角形(考点讲解),共59页。PPT课件主要包含了考场练兵,典例剖析,考点透视等内容,欢迎下载使用。
这是一份【期中复习】苏教版2019必修第二册2023-2024学年高一下册数学 专题02 三角恒等变换(考点讲解),共60页。PPT课件主要包含了考场练兵,典例剖析,考点透视等内容,欢迎下载使用。
这是一份【期中复习】人教B版2019 2023-2024学年必修第三册高一下册数学 专题02 向量的数量积与三角恒等变换(考点讲解),共60页。PPT课件主要包含了考场练兵,典例剖析,考点透视等内容,欢迎下载使用。










