






还剩52页未读,
继续阅读
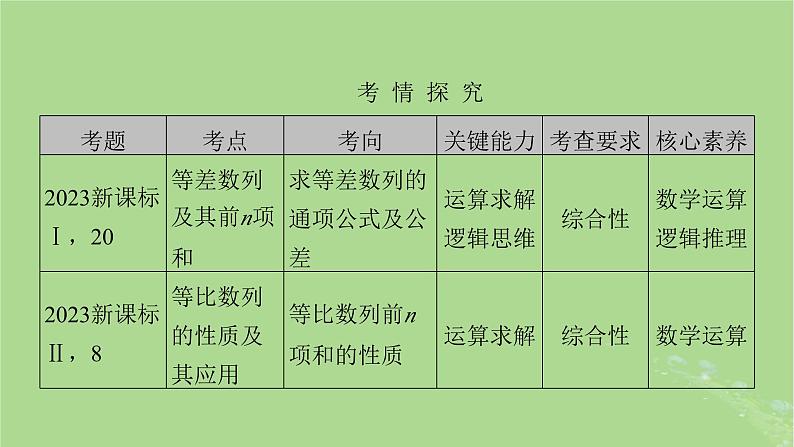
所属成套资源:2025版高考数学一轮总复习课件
成套系列资料,整套一键下载
2025版高考数学一轮总复习第6章数列第1讲数列的概念与简单表示法课件
展开
这是一份2025版高考数学一轮总复习第6章数列第1讲数列的概念与简单表示法课件,共60页。PPT课件主要包含了考情探究,一定顺序,每一个数,an=fn,a1+a2++an,nan,Sn-Sn-1,知识点四数列的分类,题组二走进教材,题组三走向高考等内容,欢迎下载使用。
【命题规律与备考策略】重点考查等差、等比数列的概念、性质、通项公式和前n项和公式,考查错位相减、裂项相消等求和方法.有时考查数列的创新问题,实际应用问题,与不等式的综合问题,考查化归与转化思想,运算求解能力.
第一讲 数列的概念与简单表示法
知识梳理 · 双基自测
知 识 梳 理知识点一 数列的有关概念
知识点二 数列的表示方法
知识点三 an与Sn的关系若数列{an}的前n项和为Sn,
归 纳 拓 展1.数列与函数数列可以看作是一个定义域为正整数集N*(或它的有限子集{1,2,…,n})的函数,当自变量从小到大依次取值时对应的一列函数值.数列的通项公式是相应函数的解析式,它的图象是一群孤立的点.
2.常见数列的通项公式(1)自然数列:1,2,3,4,…,an=n.(2)奇数列:1,3,5,7,…,an=2n-1.(3)偶数列:2,4,6,8,…,an=2n.(4)平方数列:1,4,9,16,…,an=n2.(5)2的乘方数列:2,4,8,16,…,an=2n.(6)乘积数列:2,6,12,20,…,an=n(n+1).
(8)重复数串列:9,99,999,9 999,…,an=10n-1.(9)符号数列:-1,1,-1,1,…,或1,-1,1,-1,…,an=(-1)n或an=(-1)n+1.
双 基 自 测题组一 走出误区1.判断下列结论是否正确(请在括号中打“√”或“×”)(1)所有数列的第n项都可以用公式表示出来.( )(2)依据数列的前几项归纳出数列的通项公式可能不止一个.( )(3)数列的项与项数是同一个概念.( )(4)如果数列{an}的前n项和为Sn,则对于任意n∈N*,都有an=Sn- Sn-1.( )
[解析] (1)因为数列是按一定顺序排列的一列数,如我班某次数学测试成绩,按考号从小到大的顺序排列,这个数列肯定没有通项公式,所以错误.
(3)数列{an}中第n项an,其中n为项数,an为项.(4)由数列前n项和的定义可知,当n∈N*,且n≥2都有an=Sn- Sn-1,而n=1时a1=S1,所以不正确.
3.(选修2P8T2改编)在数列{an}中,已知a1=1,a2=2且an+2=an+1+2an,则32是数列的( )A.第4项B.第5项C.第6项D.第7项[解析] 由a1=1,a2=2,得a3=a2+2a1=4,a4=a3+2a2=8,a5=a4+2a3=16,a6=a5+2a4=32.故选C.
4.(选修2P8T3改编)下列数列是递减数列的是( )
A.b1∴所求和为1+3+6=10.
考点突破 · 互动探究
由数列的前几项求数列的通项公式——自主练透
根据数列的前几项,写出下列各数列的一个通项公式an.(1)-1,7,-13,19,…;(2)3,5,9,17,33,…;(3)5,55,555,5 555,…;
[解析] (1)符号可通过(-1)n或(-1)n+1调节,其各项的绝对值的排列规律为:后面的数的绝对值总比前面数的绝对值大6,故通项公式为an=(-1)n(6n-5).(2)观察各项的特点:每一项都比2的n次幂多1,所以an=2n+1.
名师点拨:由前几项归纳数列通项公式的常用方法及具体策略1.常用方法:观察(观察规律)、比较(比较已知数列)、归纳、转化(转化为特殊数列)、联想(联想常见的数列)等.2.具体策略(1)分式中分子、分母的特征;(2)相邻项的变化特征;(3)拆项后的特征;(4)各项的符号特征和绝对值特征;
(5)化异为同.对于分式还可以考虑对分子、分母各个击破,或寻找分子、分母之间的关系;(6)对于符号交替出现的情况,可用(-1)k或(-1)k+1,k∈N*处理.注意:并不是每个数列都有通项公式,有通项公式的数列,其通项公式也不一定唯一.
由an与Sn的关系求通项公式——多维探究
角度1 已知Sn求an问题 1.若数列{an}的前n项和Sn=n2-10n,则此数列的通项公式为an=______________.[解析] 当n=1时,a1=S1=1-10=-9;当n≥2时,an=Sn-Sn-1=n2-10n-[(n-1)2-10(n-1)]=2n-11.当n=1时,2×1-11=-9=a1,所以an=2n-11.故填2n-11.
2.若数列{an}的前n项和Sn=2n+1,则此数列的通项公式为an=___________.[解析] 当n=1时,a1=S1=21+1=3;当n≥2时,an=Sn-Sn-1=(2n+1)-(2n-1+1)=2n-2n-1=2n-1.
角度2 由Sn与an的关系求an
名师点拨:已知Sn求an的一般步骤1.当n=1时,由a1=S1,求a1的值.2.当n≥2时,由an=Sn-Sn-1,求得an的表达式.3.检验a1的值是否满足2中的表达式,若不满足,则分段表示an.4.写出an的完整表达式.Sn与an关系问题的求解思路根据所求结果的不同要求,将问题向不同的两个方向转化.1.利用an=Sn-Sn-1(n≥2)转化为只含Sn,Sn-1的关系式.2.利用Sn-Sn-1=an(n≥2)转化为只含an,an-1的关系式,再求解.
【变式训练】1.(角度1)(2023·福建三明一中期中)已知Sn为数列{an}的前n项和,且lg2(Sn+1)=n+1,则数列{an}的通项公式( )
2.(角度2)(2023·辽宁部分重点高中高三联考)已知数列{an}的前n项和为Sn,满足Sn=2an-1,则{an}的通项公式为( )A.an=2n-1 B.an=2n-1C.an=2n-1 D.an=2n+1[解析] 当n=1时,S1=2a1-1=a1,∴a1=1.当n≥2时,an=Sn- Sn-1=2an-2an-1,∴an=2an-1.因此an=2n-1(n≥2).又n=1时,2n-1=1=a1,∴an=2n-1.故选B.
用累加法、累乘法求通项公式——多维探究
角度1 形如an+1=an+f(n),求an
∴an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1
角度2 形如an+1=anf(n),求an
名师点拨:1.累加法求通项公式如果数列{an}的递推公式满足an+1-an=f(n)的形式,且f(n)可求和,那么就可以运用累加法an=(an-an-1)+(an-1-an-2)+(an-2-an-3)+…+(a2-a1)+a1(n≥2),求出数列{an}的通项公式.
【变式训练】根据下列条件,写出数列{an}的通项公式:(1)(角度1)若a1=1,an+1=an+2n-1,则an=________________;(2)(角度2)若a1=1,nan-1=(n+1)an(n≥2),则an=______.
[解析] (1)∵an+1=an+2n-1,∴当n≥2时,a2-a1=1,a3-a2=3,…,an-an-1=2n-3,
又当n=1时,12-2×1+2=1,∴n=1时符合上式.∴an=n2-2n+2.
数列的函数性质——多维探究
可以看出数列的周期为4,
A.(3,+∞) B.(2,+∞)C.(1,+∞) D.(0,+∞)
角度3 数列的最大(小)项问题
名师点拨:1.解决数列周期性问题的方法:先根据已知条件求出数列的前几项,确定数列的周期,再根据周期性求值.2.判断数列单调性的方法:(1)作差(或商)法;(2)目标函数法:写出数列对应的函数,利用导数或利用基本初等函数的单调性探求其单调性,再将函数的单调性对应到数列中去.
[解析] ∵数列{an}满足a1=2,
可知此数列有周期性,周期T=3,
2.(角度2)(2024·滕州模拟)设数列{an}的通项公式为an=n2+bn,若数列{an}是单调递增数列,则实数b的取值范围为( )
[解析] ∵数列{an}是单调递增数列,∴对任意的n∈N*,都有 an+1>an,∴(n+1)2+b(n+1)>n2+bn,即b>-(2n+1)对任意的n∈N*恒成立,又n=1时,-(2n+1)取得最大值-3,∴b>-3,即实数b的取值范围为(-3,+∞).故选B.
A.此数列没有最大项B.此数列的最大项是a3C.此数列没有最小项D.此数列的最小项是a2
[解析] 令t=n-1≥0,则n=t+1,
所以数列{an}有最大项a3,有最小项a1.故选B.
名师讲坛 · 素养提升
递推数列的通项公式的求法热点一 an+1=Aan+B(A、B为常数)型 (2024·西北师大附中调研)已知数列{an}满足a1=-2,且an+1=3an+6,则an=______________.[解析] ∵an+1=3an+6,∴an+1+3=3(an+3),又a1=-2,∴a1+3=1,∴{an+3}是首项为1,公比为3的等比数列,∴an+3=3n-1,∴an=3n-1-3.
热点三 an+1=pan+f(n)(p为常数)型 (1)在数列{an}中,若a1=2,an+1=4an-3n+1,n∈N*,则an=______________.(2)若a1=1,an+1=2an+3n,n∈N*,则an=_____________.
名师点拨:1.形如an+1=pan+An+B(p、A、B为常数)的类型,可令an+1+λ(n+1)+μ=p(an+λn+μ),求出λ、μ的值即可知{an+λn+μ}为等比数列,进而可求an.
【变式训练】在数列{an}中,(1)若a1=1,an+1=3an+2,则an=________________.
(3)若a1=1,an+1=2an-3n,n∈N*,则an=__________________;(4)若a1=1,an+1=2an+3·2n,n∈N*,则an=__________________.
-5·2n-1+3n+3
(3n-2)·2n-1
[解析] (1)∵an+1=3an+2,∴an+1+1=3(an+1),又a1=1,∴a1+1=2,∴{an+1}是首项为2公比为3的等比数列,∴an+1=2×3n-1,∴an=2×3n-1-1.
∴an+1-3(n+1)-3=2(an-3n-3).又a1=1,∴{an-3n-3}是首项为-5,公比为2的等比数列,∴an-3n-3=-5·2n-1∴an=-5·2n-1+3n+3.
【命题规律与备考策略】重点考查等差、等比数列的概念、性质、通项公式和前n项和公式,考查错位相减、裂项相消等求和方法.有时考查数列的创新问题,实际应用问题,与不等式的综合问题,考查化归与转化思想,运算求解能力.
第一讲 数列的概念与简单表示法
知识梳理 · 双基自测
知 识 梳 理知识点一 数列的有关概念
知识点二 数列的表示方法
知识点三 an与Sn的关系若数列{an}的前n项和为Sn,
归 纳 拓 展1.数列与函数数列可以看作是一个定义域为正整数集N*(或它的有限子集{1,2,…,n})的函数,当自变量从小到大依次取值时对应的一列函数值.数列的通项公式是相应函数的解析式,它的图象是一群孤立的点.
2.常见数列的通项公式(1)自然数列:1,2,3,4,…,an=n.(2)奇数列:1,3,5,7,…,an=2n-1.(3)偶数列:2,4,6,8,…,an=2n.(4)平方数列:1,4,9,16,…,an=n2.(5)2的乘方数列:2,4,8,16,…,an=2n.(6)乘积数列:2,6,12,20,…,an=n(n+1).
(8)重复数串列:9,99,999,9 999,…,an=10n-1.(9)符号数列:-1,1,-1,1,…,或1,-1,1,-1,…,an=(-1)n或an=(-1)n+1.
双 基 自 测题组一 走出误区1.判断下列结论是否正确(请在括号中打“√”或“×”)(1)所有数列的第n项都可以用公式表示出来.( )(2)依据数列的前几项归纳出数列的通项公式可能不止一个.( )(3)数列的项与项数是同一个概念.( )(4)如果数列{an}的前n项和为Sn,则对于任意n∈N*,都有an=Sn- Sn-1.( )
[解析] (1)因为数列是按一定顺序排列的一列数,如我班某次数学测试成绩,按考号从小到大的顺序排列,这个数列肯定没有通项公式,所以错误.
(3)数列{an}中第n项an,其中n为项数,an为项.(4)由数列前n项和的定义可知,当n∈N*,且n≥2都有an=Sn- Sn-1,而n=1时a1=S1,所以不正确.
3.(选修2P8T2改编)在数列{an}中,已知a1=1,a2=2且an+2=an+1+2an,则32是数列的( )A.第4项B.第5项C.第6项D.第7项[解析] 由a1=1,a2=2,得a3=a2+2a1=4,a4=a3+2a2=8,a5=a4+2a3=16,a6=a5+2a4=32.故选C.
4.(选修2P8T3改编)下列数列是递减数列的是( )
A.b1
考点突破 · 互动探究
由数列的前几项求数列的通项公式——自主练透
根据数列的前几项,写出下列各数列的一个通项公式an.(1)-1,7,-13,19,…;(2)3,5,9,17,33,…;(3)5,55,555,5 555,…;
[解析] (1)符号可通过(-1)n或(-1)n+1调节,其各项的绝对值的排列规律为:后面的数的绝对值总比前面数的绝对值大6,故通项公式为an=(-1)n(6n-5).(2)观察各项的特点:每一项都比2的n次幂多1,所以an=2n+1.
名师点拨:由前几项归纳数列通项公式的常用方法及具体策略1.常用方法:观察(观察规律)、比较(比较已知数列)、归纳、转化(转化为特殊数列)、联想(联想常见的数列)等.2.具体策略(1)分式中分子、分母的特征;(2)相邻项的变化特征;(3)拆项后的特征;(4)各项的符号特征和绝对值特征;
(5)化异为同.对于分式还可以考虑对分子、分母各个击破,或寻找分子、分母之间的关系;(6)对于符号交替出现的情况,可用(-1)k或(-1)k+1,k∈N*处理.注意:并不是每个数列都有通项公式,有通项公式的数列,其通项公式也不一定唯一.
由an与Sn的关系求通项公式——多维探究
角度1 已知Sn求an问题 1.若数列{an}的前n项和Sn=n2-10n,则此数列的通项公式为an=______________.[解析] 当n=1时,a1=S1=1-10=-9;当n≥2时,an=Sn-Sn-1=n2-10n-[(n-1)2-10(n-1)]=2n-11.当n=1时,2×1-11=-9=a1,所以an=2n-11.故填2n-11.
2.若数列{an}的前n项和Sn=2n+1,则此数列的通项公式为an=___________.[解析] 当n=1时,a1=S1=21+1=3;当n≥2时,an=Sn-Sn-1=(2n+1)-(2n-1+1)=2n-2n-1=2n-1.
角度2 由Sn与an的关系求an
名师点拨:已知Sn求an的一般步骤1.当n=1时,由a1=S1,求a1的值.2.当n≥2时,由an=Sn-Sn-1,求得an的表达式.3.检验a1的值是否满足2中的表达式,若不满足,则分段表示an.4.写出an的完整表达式.Sn与an关系问题的求解思路根据所求结果的不同要求,将问题向不同的两个方向转化.1.利用an=Sn-Sn-1(n≥2)转化为只含Sn,Sn-1的关系式.2.利用Sn-Sn-1=an(n≥2)转化为只含an,an-1的关系式,再求解.
【变式训练】1.(角度1)(2023·福建三明一中期中)已知Sn为数列{an}的前n项和,且lg2(Sn+1)=n+1,则数列{an}的通项公式( )
2.(角度2)(2023·辽宁部分重点高中高三联考)已知数列{an}的前n项和为Sn,满足Sn=2an-1,则{an}的通项公式为( )A.an=2n-1 B.an=2n-1C.an=2n-1 D.an=2n+1[解析] 当n=1时,S1=2a1-1=a1,∴a1=1.当n≥2时,an=Sn- Sn-1=2an-2an-1,∴an=2an-1.因此an=2n-1(n≥2).又n=1时,2n-1=1=a1,∴an=2n-1.故选B.
用累加法、累乘法求通项公式——多维探究
角度1 形如an+1=an+f(n),求an
∴an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1
角度2 形如an+1=anf(n),求an
名师点拨:1.累加法求通项公式如果数列{an}的递推公式满足an+1-an=f(n)的形式,且f(n)可求和,那么就可以运用累加法an=(an-an-1)+(an-1-an-2)+(an-2-an-3)+…+(a2-a1)+a1(n≥2),求出数列{an}的通项公式.
【变式训练】根据下列条件,写出数列{an}的通项公式:(1)(角度1)若a1=1,an+1=an+2n-1,则an=________________;(2)(角度2)若a1=1,nan-1=(n+1)an(n≥2),则an=______.
[解析] (1)∵an+1=an+2n-1,∴当n≥2时,a2-a1=1,a3-a2=3,…,an-an-1=2n-3,
又当n=1时,12-2×1+2=1,∴n=1时符合上式.∴an=n2-2n+2.
数列的函数性质——多维探究
可以看出数列的周期为4,
A.(3,+∞) B.(2,+∞)C.(1,+∞) D.(0,+∞)
角度3 数列的最大(小)项问题
名师点拨:1.解决数列周期性问题的方法:先根据已知条件求出数列的前几项,确定数列的周期,再根据周期性求值.2.判断数列单调性的方法:(1)作差(或商)法;(2)目标函数法:写出数列对应的函数,利用导数或利用基本初等函数的单调性探求其单调性,再将函数的单调性对应到数列中去.
[解析] ∵数列{an}满足a1=2,
可知此数列有周期性,周期T=3,
2.(角度2)(2024·滕州模拟)设数列{an}的通项公式为an=n2+bn,若数列{an}是单调递增数列,则实数b的取值范围为( )
[解析] ∵数列{an}是单调递增数列,∴对任意的n∈N*,都有 an+1>an,∴(n+1)2+b(n+1)>n2+bn,即b>-(2n+1)对任意的n∈N*恒成立,又n=1时,-(2n+1)取得最大值-3,∴b>-3,即实数b的取值范围为(-3,+∞).故选B.
A.此数列没有最大项B.此数列的最大项是a3C.此数列没有最小项D.此数列的最小项是a2
[解析] 令t=n-1≥0,则n=t+1,
所以数列{an}有最大项a3,有最小项a1.故选B.
名师讲坛 · 素养提升
递推数列的通项公式的求法热点一 an+1=Aan+B(A、B为常数)型 (2024·西北师大附中调研)已知数列{an}满足a1=-2,且an+1=3an+6,则an=______________.[解析] ∵an+1=3an+6,∴an+1+3=3(an+3),又a1=-2,∴a1+3=1,∴{an+3}是首项为1,公比为3的等比数列,∴an+3=3n-1,∴an=3n-1-3.
热点三 an+1=pan+f(n)(p为常数)型 (1)在数列{an}中,若a1=2,an+1=4an-3n+1,n∈N*,则an=______________.(2)若a1=1,an+1=2an+3n,n∈N*,则an=_____________.
名师点拨:1.形如an+1=pan+An+B(p、A、B为常数)的类型,可令an+1+λ(n+1)+μ=p(an+λn+μ),求出λ、μ的值即可知{an+λn+μ}为等比数列,进而可求an.
【变式训练】在数列{an}中,(1)若a1=1,an+1=3an+2,则an=________________.
(3)若a1=1,an+1=2an-3n,n∈N*,则an=__________________;(4)若a1=1,an+1=2an+3·2n,n∈N*,则an=__________________.
-5·2n-1+3n+3
(3n-2)·2n-1
[解析] (1)∵an+1=3an+2,∴an+1+1=3(an+1),又a1=1,∴a1+1=2,∴{an+1}是首项为2公比为3的等比数列,∴an+1=2×3n-1,∴an=2×3n-1-1.
∴an+1-3(n+1)-3=2(an-3n-3).又a1=1,∴{an-3n-3}是首项为-5,公比为2的等比数列,∴an-3n-3=-5·2n-1∴an=-5·2n-1+3n+3.



![《高考总复习》数学 第五章 第1讲 数列的概念与简单表示法[配套课件]](http://jx-previews-01.oss-cn-hangzhou.aliyuncs.com/3/3/13744227/0/0.jpg?x-oss-process=image/resize,w_202)








