





2025版高考数学一轮总复习第1章集合常用逻辑用语不等式第3讲不等关系与不等式课件
展开知识梳理 · 双基自测
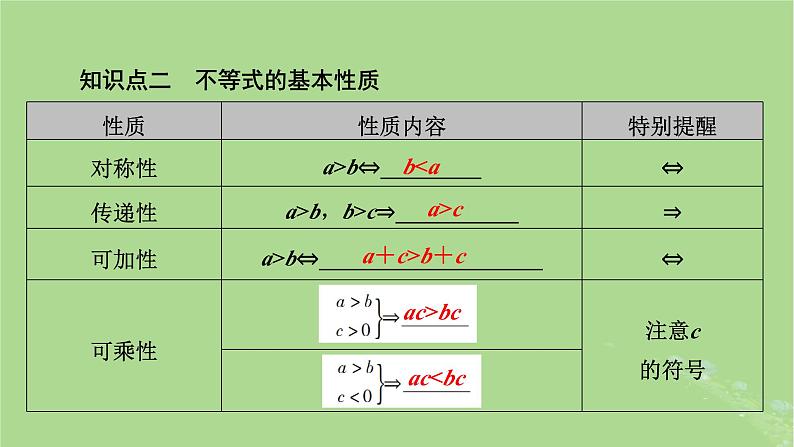
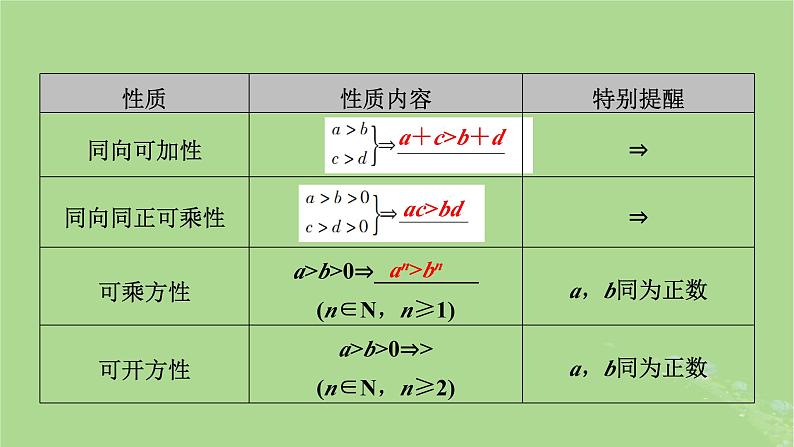
知识点二 不等式的基本性质
题组二 走进教材2.(必修1P14T5)某班有学生参加才艺比赛,已知每人只参加一个比赛,且参加书法比赛的人数多于参加唱歌比赛的人数,参加唱歌比赛的人数多于参加折纸比赛的人数,参加折纸比赛的人数的2倍多于参加书法比赛的人数,则参加这三项比赛的总人数至少为( )A.7 B.9C.12 D.15[解析] 设参加书法、唱歌、折纸比赛的人数分别为a,b,c,由题意得a≥b+1,b≥c+1,2c≥a+1,∴a+b+2c≥b+1+c+1+a+1,∴c≥3,∴b≥4,a≥5,∴参加这三项比赛的总人数至少为12.故选C.
题组三 走向高考5.(2022·上海卷)已知实数a,b,c,d满足:a>b>c>d,则下列选项中正确的是( )A.a+d>b+c B.a+c>b+dC.ad>bc D.ac>bd
[解析] 选项A,如取a=4,b=3,c=2,d=-4,此时a+d
比较代数式的大小——自主练透
比较代数式的大小——自主练透 1.已知0
名师点拨:比较两实数大小的方法1.作差(商)法:作差(商)⇒变形⇒判断.2.构造函数法:利用函数的单调性比较大小.3.中间量法:利用中间量法比较两式大小,一般选取“0”或“1”作为中间量.
不等式的性质及应用——多维探究
名师点拨:1.在判断一个关于不等式命题的真假时,先把要判断的命题和不等式的性质联系起来考虑,找到与命题相近的性质,并根据性质判断命题的真假,有时还要用到其他知识,如本例中幂函数、对数函数的性质等.2.在应用不等式的性质时,不可以强化或弱化不等式成立的条件,如“同向不等式”才可以相加,“同向正数不等式”才可以相乘.3.在不等关系的判断中,赋值法是非常有效的方法.
名师点拨:利用不等式性质可以求某些代数式的取值范围,但应注意两点:一是必须严格运用不等式的性质;二是在多次运用不等式的性质时有可能扩大了变量的取值范围.解决的途径是先建立所求范围的整体与已知范围的整体的等量关系,最后通过“一次性”不等关系的运算求解范围.
【变式训练】1.(角度1)(多选题)(2023·张家口一模)若a>b,则下列不等式中正确的有( )A.a-b>0 B.2a>2bC.ac>bc D.a2>b2
[解析] 对于A,因为a>b,所以a-b>0,故A正确;对于B,因为a>b,且指数函数y=2x在R上单调递增,所以2a>2b,故B正确;对于C,若c<0,则ac
2.设a>b>0,下列各数小于1的是( )
名师点拨:特殊值法比较大小的思路利用特殊值法比较不等式的大小时需要注意以下问题:选择项两数大小是确定的,如果出现两数大小由某个参数确定或大小不确定的选项,就无法通过特殊值进行检验;赋值应该满足前提条件:当一次赋值不能确定准确的选项,则可以通过二次赋值检验,直至得到正确选项.
[解析] 解法一:因为实数x,y满足ax
2.(2023·郑州模拟)设x>0,P=2x+2-x,Q=(sin x+cs x)2,则( )A.P>Q B.P
【变式训练】 (多选题)(2023·重庆一中模拟)下列不等式成立的是( )
[解析] 因为a,b∈(0,1),则aπ,bπ∈(0,π),而函数y=cs x在(0,π)上单调递减,又cs aπ
名师点拨:1.利用函数性质比较数、式的大小,得到函数的单调区间是问题求解的关键,解题时,指数、对数、三角函数单调性的运用是解题的主要形式.2.通过对称性、周期性,可以将比较大小的数、式转化到同一个单调区间,有利于其大小比较.3.导数工具的应用,拓宽了这类问题的命题形式和解题难度,值得我们关注和重视.
【变式训练】 (多选题)(2023·邯郸高三期末)设0
2025版高考数学一轮总复习第1章集合常用逻辑用语不等式第5讲基本不等式课件: 这是一份2025版高考数学一轮总复习第1章集合常用逻辑用语不等式第5讲基本不等式课件,共60页。PPT课件主要包含了a=b,a0b0,算术平均数,几何平均数,x=y,ABD,m=2n等内容,欢迎下载使用。
2025版高考数学一轮总复习第1章集合常用逻辑用语不等式第2讲常用逻辑用语课件: 这是一份2025版高考数学一轮总复习第1章集合常用逻辑用语不等式第2讲常用逻辑用语课件,共60页。PPT课件主要包含了充分不必要,必要不充分,既不充分也不必要,判断真假,全称量词,存在量词,ABD等内容,欢迎下载使用。
2025版高考数学一轮总复习第1章集合常用逻辑用语不等式第1讲集合课件: 这是一份2025版高考数学一轮总复习第1章集合常用逻辑用语不等式第1讲集合课件,共55页。PPT课件主要包含了考情探究,第一讲集合,列举法,描述法,图示法,正整数,整数集,有理数集,B中的元素,不属于A等内容,欢迎下载使用。












