高中数学人教B版 (2019)选择性必修 第一册第一章　空间向量与立体几何1.2 空间向量在立体几何中的应用1.2.1 空间中的点、直线与空间向量课后测评

这是一份高中数学人教B版 (2019)选择性必修 第一册第一章　空间向量与立体几何1.2 空间向量在立体几何中的应用1.2.1 空间中的点、直线与空间向量课后测评，共10页。
1．在正方体ABCD﹣A1B1C1D1中，点E是棱AB的中点，点F是四边形CDD1C1所在平面内的一点，且AF⊥B1E，则点F为（ ）
A．一条直线上任意一点B．一个平面上任意一点
C．一个圆上任意一点D．一个椭圆上任意一点
2．直线l的一方向向量为（2，3），则它的斜率k为（ ）
A．B．C．D．
3．若A（2，1，1），B（1，2，2）在直线l上，则直线l的一个方向向量为（ ）
A．（2，1，2）B．（﹣2，2，3）C．（﹣1，1，1）D．（1，0，0）
4．若A（0，1，2），B（2，5，8）在直线l上，则直线l的一个方向向量为（ ）
A．（3，2，1）B．（1，3，2）C．（2，1，3）D．（1，2，3）
5．已知向量＝（sinθ﹣1，1），＝（csθ，1），θ∈[﹣，﹣]，且，则θ的值为（ ）
A．﹣B．C．D．
6．已知＝（1，5，﹣2），＝（3，1，z），若⊥，＝（x﹣1，y，﹣3），且BP⊥平面ABC，则实数x、y、z分别为（ ）
A．，﹣，4B．，﹣，4C．，﹣2，4D．4，，﹣15
7．平面α的法向量，平面β的法向量，已知α∥β，则x+y＝（ ）
A．B．C．3D．
8．若平面α与β的法向量分别是＝（2，4，﹣3），＝（﹣1，2，2），则平面α与β的位置关系是（ ）
A．平行B．垂直
C．相交但不垂直D．无法确定
9．平面α的一个法向量为（1，2，0），平面β的一个法向量为（2，﹣1，0），则平面α与平面β的位置关系是（ ）
A．平行B．相交但不垂直
C．垂直D．不能确定
10．若直线l的方向向量为＝（1，0，2），平面α的法向量为＝（﹣2，0，﹣4），则直线l与平面α的位置关系为（ ）
A．平行B．垂直C．在平面内D．斜交
二．填空题
11．在棱长为6的正方体ABCD﹣A1B1C1D1中，点M是线段BC的中点，P是正方形DCC1D1（包括边界）上运动，且满足∠APD＝∠MPC，则P点的轨迹周长为 ．
12．已知直线l过点A（3，2，1），B（2，2，2），且＝（2，0，x）是直线l的一个方向向量，则x＝ ．
13．已知向量＝（x，3），＝（4，6），若，则实数x的值为 ；若⊥，则实数x的值为 ．
14．已知平面α，β的法向量分别为＝（1，y，4），＝（x，﹣1，﹣2），若a⊥β，则x﹣y的值为 ．
15．已知点A（3，2，1），点B（﹣1，4，3），线段AB中点为M，O为坐标原点，则|OM|＝ ．
三．解答题
16．（1）用符号表示下来语句，并画出同时满足这四个语句的一个几何图形：
①直线l在平面α内；
②直线m不在平面α内；
③直线m与平面α交于点A；
④直线l不经过点A．
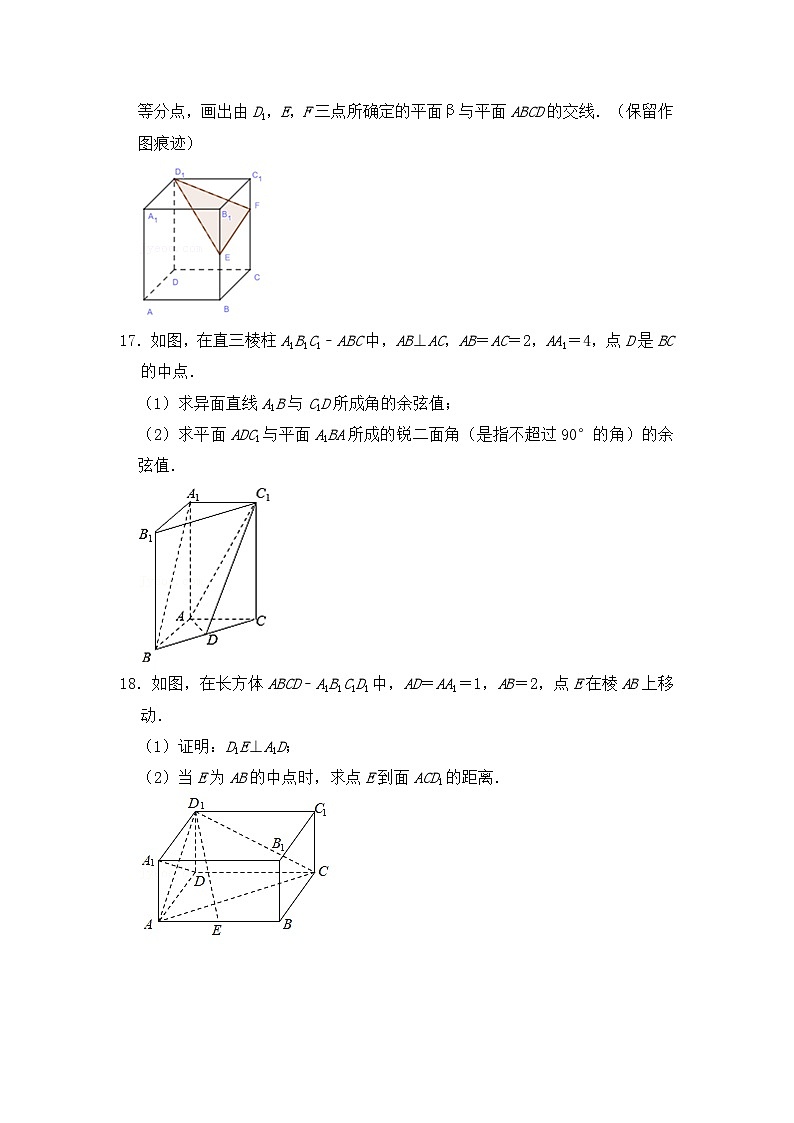
（2）如图，在长方体ABCD﹣A1B1C1D1中，E为棱BB1的中点，F为棱CC1的三等分点，画出由D1，E，F三点所确定的平面β与平面ABCD的交线．（保留作图痕迹）
17．如图，在直三棱柱A1B1C1﹣ABC中，AB⊥AC，AB＝AC＝2，AA1＝4，点D是BC的中点．
（1）求异面直线A1B与C1D所成角的余弦值；
（2）求平面ADC1与平面A1BA所成的锐二面角（是指不超过90°的角）的余弦值．
18．如图，在长方体ABCD﹣A1B1C1D1中，AD＝AA1＝1，AB＝2，点E在棱AB上移动．
（1）证明：D1E⊥A1D；
（2）当E为AB的中点时，求点E到面ACD1的距离．
人教B版（2019）数学高中选择性必修第一册
1.2.1 空间中的点、直线与空间向量
参考答案与试题解析
一．选择题
1．【考点】空间点、线、面的位置．
【解答】解：在正方体ABCD﹣A1B1C1D1中，因为AF⊥B1E，
所以F在过点A且与B1E垂直的一个平面α内，即为平面α的一个法向量，
又平面CDD1C11法向量为，与不平行，
所以平面α与平面CDD1C1一定相交于直线l，所以点F在直线l上运动．
故选：A．
2．【考点】直线的方向向量、空间直线的向量参数方程；直线的斜率．
【解答】解：∵，（1，k）是直线的方向向量，
∴，
故选：A．
3．【考点】直线的方向向量、空间直线的向量参数方程．
【解答】解：A（2，1，1），B（1，2，2）在直线l上，
则直线l的一个方向向量为＝（﹣1，1，1）．
故选：C．
4．【考点】直线的方向向量、空间直线的向量参数方程．
【解答】解：A（0，1，2），B（2，5，8）在直线l上，
则直线l的一个方向向量为：
＝（2，4，6）＝（1，2，3），
故选：D．
5．【考点】向量语言表述线线的垂直、平行关系．
【解答】解：由题意可得sinθ﹣1﹣csθ＝0，即sinθ﹣csθ＝1，
所以2sin（θ﹣）＝1，sin（θ﹣）＝，
因为θ∈[﹣，﹣]，所以θ﹣∈[﹣2π，﹣]，
所以θ﹣＝﹣，
所以θ＝﹣．
故选：C．
6．【考点】向量语言表述线线的垂直、平行关系．
【解答】解：∵⊥，
∴＝3+5﹣2Z＝0，解得z＝4．
∴．
∵BP⊥平面ABC，
∴，．
∴化为，
解得．
∴，，z＝4．
故选：B．
7．【考点】向量语言表述面面的垂直、平行关系．
【解答】解：根据题意，α∥β，则有∥，
则有＝＝，解可得x＝4，y＝﹣，
则x+y＝；
故选：A．
8．【考点】向量语言表述面面的垂直、平行关系．
【解答】解：＝﹣2+8﹣6＝0
∴⊥
∴平面α与平面β垂直
故选：B．
9．【考点】空间点、线、面的位置．
【解答】解：由题意可得（1，2，0）•（2，﹣1，0）＝1×2﹣2×1+0×0＝0，
故两个平面的法向量垂直，故平面α和平面β的位置关系为垂直，
故选：C．
10．【考点】空间点、线、面的位置．
【解答】解：直线l的方向向量为＝（1，0，2），
平面α的法向量为＝（﹣2，0，﹣4），
∵＝﹣2，∴∥，
∴直线l与平面α的位置关系为垂直．
故选：B．
二．填空题
11．【考点】空间点、线、面的位置．
【解答】解：如图，在棱长为6的正方体ABCD﹣A1B1C1D1中，
则AD⊥平面DCC1D1，MC⊥平面DCC1D1，
又DP，PC在平面DCC1D1上，
∴AD⊥DP，MC⊥CP，又∠APD＝∠MPC，
∴Rt△ADP～Rt△MCP，
∴＝2，即PD＝2PC，
如图，在平面DCC1D1中，以D为原点，DC，DD1分别为x，y轴建立平面直角坐标系，
则D（0，0），C（6，0），P（x，y），由PD＝2PC，知，
化简整理得（x﹣8）2+y2＝16，0≤x≤6，圆心（8，0），半径r＝4的圆，
所以P点的轨迹为圆（x﹣8）2+y2＝16与四边形DCC1D1的交点，
即为图中的，其中，CM＝2，FM＝4，则∠FMC＝，
由弧长公式知，
故答案为：．
12．【考点】直线的方向向量、空间直线的向量参数方程．
【解答】解：直线l过点A（3，2，1），B（2，2，2），且＝（2，0，x）是直线l的一个方向向量，
∴＝（﹣1，0，1），∴∥，
∴x＝﹣2．
故答案为：﹣2．
13．【考点】向量语言表述线线的垂直、平行关系．
【解答】解：向量＝（x，3），＝（4，6），
若，则6x﹣3×4＝0，解得x＝2；
若⊥，则4x+3×6＝0，解得x＝﹣．
故答案为：2；﹣．
14．【考点】向量语言表述面面的垂直、平行关系．
【解答】解：根据题意，平面α，β的法向量分别为＝（1，y，4），＝（x，﹣1，﹣2），
若a⊥β，则有•＝x﹣y﹣8＝0，即x﹣y＝8．
故答案为：8．
15．【考点】空间点、线、面的位置．
【解答】解：∵点A（3，2，1），点B（﹣1，4，3），
线段AB中点为M，O为坐标原点，
∴M（1，3，2），
∴|OM|＝＝．
故答案为：．
三．解答题
16．【考点】空间点、线、面的位置；平面的基本性质及推论；空间中直线与直线之间的位置关系．
【解答】解：（1）l⊂α；m⊄α；m∩α＝A；A∉l；示意图如下：
（2）如图，分别延长DB，D1E相交于点L，
分别延长DC，D1F相交于点I，
直线IL即为所求．
17．【考点】直线的方向向量、空间直线的向量参数方程；二面角的平面角及求法；异面直线及其所成的角．
【解答】解：（1）以{，，}为单位正交基底建立空间直角坐标系A﹣xyz，
则由题意知A（0，0，0），B（2，0，0），C（0，2，0），
A1（0，0，4），D（1，1，0），C1（0，2，4），
∴＝（2，0，﹣4），＝（1，﹣1，﹣4），
∴cs＜，＞＝＝＝，
∴异面直线A1B与C1D所成角的余弦值为．
（2）是平面ABA1的一个法向量，
设平面ADC1的法向量为，
∵，
∴，取z＝1，得y＝﹣2，x＝2，
∴平面ADC1的法向量为＝（2，﹣2，1），
设平面ADC1与ABA1所成二面角为θ，
∴csθ＝|cs＜，＞|＝||＝，
∴平面ADC1与ABA1所成二面角的余弦值为：．
18．【考点】向量语言表述线线的垂直、平行关系；点、线、面间的距离计算．
【解答】解：（1）分别以DA、DC、DD1所在直线为x、y、z轴，建立如图的坐标系，则D（0，0，0），A1（1，0，1），D1（0，0，1），A（1，0，0）
所以，设E（1，t，0），
所以，，
∴D1E⊥A1D；
（2）当E为AB的中点时，E（1，1，0），，
设平面ACD1的法向量是，
求出，，
由，得
∵＝（1，1，﹣1）
由点到平面的距离公式，得，
∴点E到面ACD1的距离是．