人教B版 (2019)选择性必修 第一册1.2.3 直线与平面的夹角复习练习题

这是一份人教B版 (2019)选择性必修 第一册1.2.3 直线与平面的夹角复习练习题，共22页。

1．在正三棱锥P﹣ABC中，D是棱PC上的点，且PD＝2DC．设PB，PC与平面ABD所成的角分别为α，β，则sinα：sinβ＝（ ）
A．B．C．D．
2．在直三棱柱ABC﹣A1B1C1中，底面是等腰直角三角形，，点D在棱BB1上，且，则AD与平面AA1C1C所成角的正弦值为（ ）
A．B．C．D．
3．已知三棱柱ABC﹣A1B1C1的所有棱长均为2，该三棱柱体积等于3，则直线AA1和平面ABC所成角的大小为（ ）
A．90°B．30°C．45°D．60°
4．已知在空间直角坐标系Oxyz（O为坐标原点）中，点A（1，1，﹣1）关于x轴的对称点为点B，则z轴与平面OAB所成的线面角为（ ）
A．B．C．D．
5．在空间直角坐标系O﹣xyz中，经过点P0（x0，y0，z0），以为法向量的平面方程为a（x﹣x0）+b（y﹣y0）+c（z﹣z0）＝0，经过点P0（x0，y0，z0），且一个方向向量为的直线l方程为．已知在空间直角坐标系O﹣xyz中，平面α的方程为x﹣2y+3z＝0，直线l的方程为，则直线l与平面α所成角的正弦值为（ ）
A．B．C．D．
6．已知三棱锥S﹣ABC的所有顶点都在表面积为64π的球面上，且SA⊥平面ABC，SA＝4，，，M是边BC上一动点，则直线SM与平面ABC所成的最大角的正切值为（ ）
A．3B．C．D．
7．如图，在正方体ABCD﹣A1B1C1D1中，E为AB的中点，则直线A1E与平面A1BC1所成角的正弦值为（ ）
A．B．C．D．
8．在长方体ABCD﹣A1B1C1D1中，AB＝BC＝1，，则直线AC1与平面BB1C1C所成角的大小为（ ）
A．30°B．45°C．60°D．90°
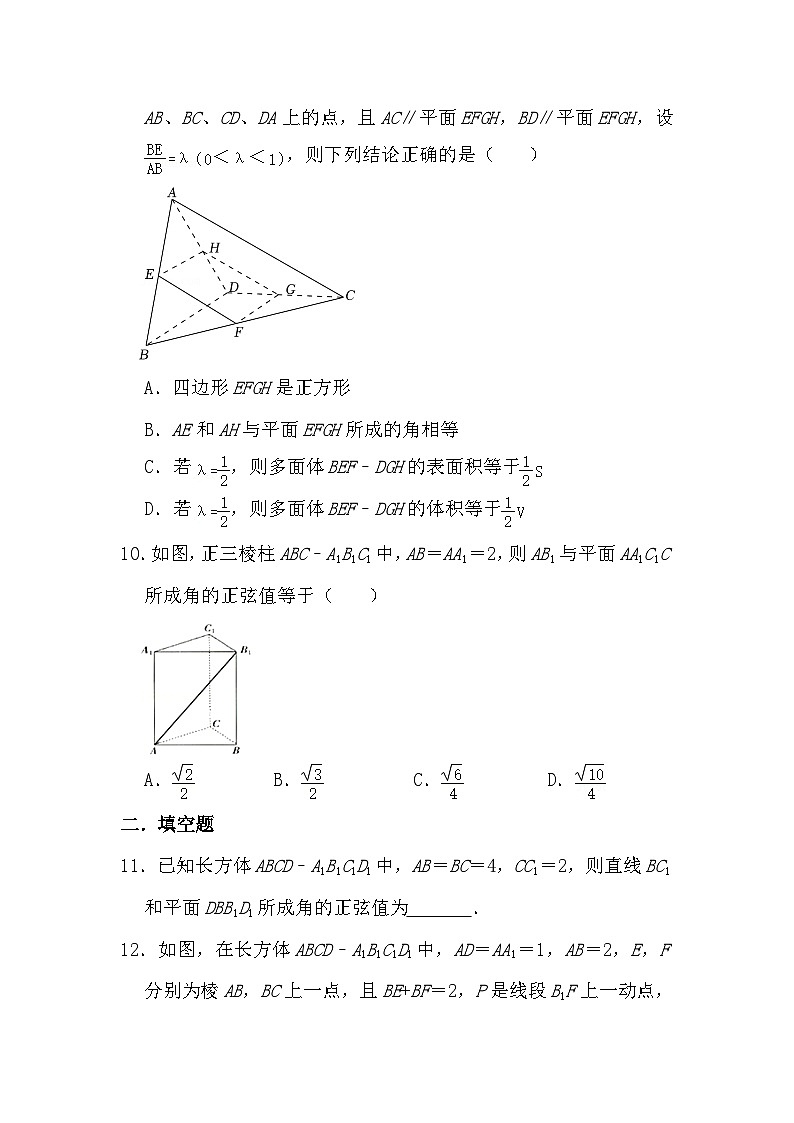
9．如图，四面体ABCD的表面积为S，体积为V，E、F、G、H分别是AB、BC、CD、DA上的点，且AC∥平面EFGH，BD∥平面EFGH，设，则下列结论正确的是（ ）
A．四边形EFGH是正方形
B．AE和AH与平面EFGH所成的角相等
C．若，则多面体BEF﹣DGH的表面积等于
D．若，则多面体BEF﹣DGH的体积等于
10．如图，正三棱柱ABC﹣A1B1C1中，AB＝AA1＝2，则AB1与平面AA1C1C所成角的正弦值等于（ ）
A．B．C．D．
二．填空题
11．已知长方体ABCD﹣A1B1C1D1中，AB＝BC＝4，CC1＝2，则直线BC1和平面DBB1D1所成角的正弦值为 ．
12．如图，在长方体ABCD﹣A1B1C1D1中，AD＝AA1＝1，AB＝2，E，F分别为棱AB，BC上一点，且BE+BF＝2，P是线段B1F上一动点，当三棱锥B1﹣EBF的体积最大时，直线D1P与平面B1EC所成角的正弦值的取值范围为 ．
13．已知一个圆锥的底面半径为1cm，侧面积为2πcm2，则该圆锥的母线与底面所成的角的大小为 ．
14．在三棱锥P﹣ABC中，PA⊥底面ABC，PA＝1，AB＝BC＝3，，则PB与平面PAC所成角的正切值为 ．
15．已知正三棱柱ABC﹣A1B1C1的所有棱长都相等，则AC1与平面BB1C1C所成角的余弦值为 ．
三．解答题
16．如图，在圆锥PO中，边长为的正△ABC内接于圆O，AD为圆O的直径，E为线段PD的中点．
（1）求证：直线PO∥平面BCE；
（2）若AE⊥PD，求直线AP与平面ABE所成角的正弦值．
17．如图，在多面体ABCDEF中，ABCD为正方形，DE⊥平面ABCD，CF∥DE，DE＝DC＝2CF＝2．
（Ⅰ）求证：BF∥平面ADE；
（Ⅱ）求直线BD与平面AEF所成角的大小．
18．如图，在正四棱锥P﹣ABCD中，O为底面中心，PO＝AO＝3，M为PO中点，＝2．
（1）求证：DM∥平面EAC；
（2）求：（ⅰ）直线DM到平面EAC的距离；
（ⅱ）求直线MA与平面EAC所成角的正弦值．
人教B版（2019）数学高中选择性必修第一册
1.2.3 直线与平面的夹角
参考答案与试题解析
一．选择题
1．【考点】直线与平面所成的角．
【解答】解：设点P到平面ABD的距离为h，则sinα＝，
∵D是棱PC上的点，且PD＝2DC，
∴PD和PC与平面ABD所成的角相等，
∴sinβ＝，
∴＝＝＝＝．
故选：D．
2．【考点】直线与平面所成的角．
【解答】解：如图，取AC的中点M，∵BA＝BC＝3，∠ABC＝90°，
则AC＝6，BM＝3，BM⊥AC，
过点M作MN∥BD，且使得MN＝BD＝，
则四边形BDNM是平行四边形，∴DN∥BM，DN＝BM＝3，
由题意，BD⊥平面ABC，则MN⊥平面ABC，
而BM⊂平面ABC，∴MN⊥BM，
又BM⊥AC，AC∩MN＝M，∴BM⊥平面AA1C1C，∵DN∥BM，∴DN⊥平面AA1C1C，
连接DA，NA，则∠DAN是AD与平面AA1C1C所成的角，
∵AD＝＝2，∴sin∠DAN＝＝＝，
∴AD与平面AA1C1C所成角的正弦值为．
故选：C．
3．【考点】直线与平面所成的角．
【解答】解：设三棱柱ABC﹣A1B1C1的高为h，
因为三棱柱ABC﹣A1B1C1的所有棱长均为2，该三棱柱体积等于3，
所以三棱柱体积，解得，
所以过A1点作底面ABC的垂线A1H，垂足为H，则，
连接AH，则∠A1AH是直线AA1和平面ABC所成角，
所以，
由于，所以∠A1AH＝60°．
故选：D．
4．【考点】直线与平面所成的角．
【解答】解：在空间直角坐标系Oxyz（O为坐标原点）中，
点A（1，1，﹣1）关于x轴的对称点为点B，
∴B（1，﹣1，1），＝（1，1，﹣1），＝（1，﹣1，1），
设平面OAB的法向量＝（x，y，z），
则，取y＝1，得＝（0，1，1），
在z轴上取C（0，0，1），＝（0，0，1），
设z轴与平面OAB所成的线面角为θ，
则sinθ＝＝＝，
∴θ＝，
∴z轴与平面OAB所成的线面角为．
故选：B．
5．【考点】直线与平面所成的角．
【解答】解：∵经过P（﹣1，2，0）的直线l方程为，
则直线l的一个方向向量为＝（2，3，1），
又平面α的方程为x﹣2y+3z＝0，
则平面α的一个法向量为＝（1，﹣2，3），
∴|cs＜＞|＝＝，
则直线l与平面α所成角的正弦值为．
故选：A．
6．【考点】直线与平面所成的角．
【解答】解：根据题意：设外接球的半径为r，则4πr2＝64π，∴r＝4，
设外接球的球心为O，则O在平面ABC内的投影O′为三角形ABC的外心，
SA⊥平面ABC，SA＝4，所以OS2＝22+O′A2，
从而AO′＝2，所以＝＝2R＝4，
解得sinC＝，BC＝6，又，∴C＝，∴B＝，
M是边BC上一动点，SM与平面ABC内的射影最短时，直线SM与平面ABC所成的最大，
此时AM⊥BC，易求AM长的最小值为，
所以直线SM与平面ABC所成的最大角的正切值为＝．
故选：B．
7．【考点】直线与平面所成的角．
【解答】解：设正方体A1B1C1D1﹣ABCD的棱长为2，
以D为原点，DA为x轴，DC为y轴，DD1为z轴，建立空间直角坐标系，
∵E为AB中点，∴A1（2，0，2），E（2，1，0），
B（2，2，0），A1（2，0，2），C1（0，2，2），
＝（﹣2，2，0），＝（0，2，﹣2），＝（0，1，﹣2），
设平面A1C1B的法向量＝（x，y，z），
则，取x＝1，得＝（1，1，1），
设直线A1E与平面A1C1B所成角为θ，
则sinθ＝|cs＜，＞|＝||＝||＝．
∴直线A1E与平面A1C1B所成角的正弦值为．
故选：D．
8．【考点】直线与平面所成的角．
【解答】解：连接BC1，由长方体ABCD﹣A1B1C1D1，可得AB⊥平面BB1C1C，
所以AC1在平面BB1C1C的射影为BC1，
所以∠AC1B为直线AC1与平面BB1C1C所成的角，
由AB＝BC＝1，，
可得BC1＝＝，AC1＝＝2，
在Rt△ABC1中，cs∠AC1B＝＝，
所以直线AC1与平面BB1C1C所成角的大小为30°．
故选：A．
9．【考点】直线与平面所成的角；棱柱、棱锥、棱台的体积．
【解答】解：对A，因为AC∥平面EFGH，AC⊂平面ABC，
EF⊂平面EFGH，平面EFGH⋂平面ABC＝EF，所以AC∥EF，同理AC∥GH，
所以EF∥GH，同理EH∥FG，
所以四边形EFGH是平行四边形．
所以四边形EFGH不一定是正方形，所以选项A错误；
对B，如果AE和AH与平面EFGH所成的角相等，则AE＝AH，则AB＝AD，
已知中没有AB＝AD，所以AE和AH与平面EFGH所成的角不一定相等，所以选项B错误；
对C，假设正四面体ABCD，AB＝2，取BD的中点N，
连接AN，CN．则BD⊥AN，BD⊥CN，
因为AN⋂CN＝N，AN，CN⊂平面ACN，所以BD⊥平面ACN，
所以BD⊥AC，所以EF⊥FG，
前面已经证明四边形EFGH是平行四边形，
又EF＝FG，所以四边形EFGH是正方形，且EF＝FG＝1，
正四面体的每一个面的面积为，
所以正四面体的表面积为，
所以多面体BEF﹣DGH的表面积，
所以选项C错误；
对D，如图，设BD中点为M，连接EM，MF，则多面体EMF﹣HDG是棱柱，
设点B到平面EMF的距离为h1，由于，所以点E是AB的中点，
则点M到平面HDC的距离为h1，点B到平面ADC的距离为2h1．
则多面体BEF﹣DGH的体积＝＝，
所以选项D正确．
故选：D．
10．【考点】直线与平面所成的角．
【解答】解：如图，
∵ABC﹣A1B1C1是正三棱柱，∴平面A1B1C1⊥平面AA1C1C，
取A1C1的中点O，连接AO，B1O，则B1O⊥A1C1，可得B1O⊥平面AA1C1C，
即∠B1AO为AB1与平面AA1C1C所成角．
∵AB＝AA1＝2，∴，，
可得sin，
∴AB1与平面AA1C1C所成角的正弦值为．
故选：C．
二．填空题
11．【考点】直线与平面所成的角．
【解答】解：由题意，连接A1C1，交B1D1于点O
∵长方体ABCD﹣A1B1C1D1中，AB＝BC＝4
∴C1O⊥B1D1
∴C1O⊥平面DBB1D1
在Rt△BOC1中，
∴直线BC1和平面DBB1D1所成角的正弦值为．
故答案为：．
12．【考点】直线与平面所成的角．
【解答】解：当三棱锥B1﹣EBF的体积最大时，△EBF的面积取最大值，，
当且仅当BE＝BF＝1时，等号成立，此时，E为AB的中点，F与C重合．
如图，以D为坐标原点，DA，DC，DD1所在直线分别为x轴、y轴、z轴建立空间直角坐标系，
则D1（0，0，1），B1（1，2，1），E（1，1，0），C（0，2，0），，．
设平面B1EC的法向量为，∴可取x＝1，得．
设，λ∈[0，1]，∴P（λ，2，λ），∴．
设直线D1P与平面B1EC所成的角为θ，
∴．
∵λ∈[0，1]，∴当时，sinθ的最大值为；当λ＝0或1时，sinθ的最小值为，
∴直线D1P与平面B1EC所成角的正弦值的取值范围为．
故答案为：．
13．【考点】直线与平面所成的角．
【解答】解：如图，
圆锥的底面半径为1，设母线长为l，
则圆锥的侧面积S＝，得l＝2．
设母线与底面所成角为θ，则csθ＝，
∴θ＝，
故答案为：．
14．【考点】直线与平面所成的角．
【解答】解：以A为原点，在平面ABC内作垂直于AC的射线为x轴，以射线AC为y轴，
射线AP为z轴建立如图所示空间直角坐标系，如图所示：
则P（0，0，1），B（1，2，0），C（0，4，0），
所以＝（1，2，﹣1），
由x轴⊥平面PAC得平面PAC的一个法向量为＝（1，0，0），
设直线PB与平面PAC所成的角为α，
则sinα＝|cs＜，＞|＝||＝＝，
α∈（0，），csα＝＝，
所以PB与平面PAC所成角的正切值为tanα＝＝．
故答案为：．
15．【考点】直线与平面所成的角．
【解答】解：取BC的中点E，连接C1E，AE，则AE⊥BC，
∵正三棱柱ABC﹣A1B1C1中，面ABC⊥面BB1C1C，面ABC∩面BB1C1C＝BC，
∴AE⊥面BB1C1C，
∴∠AC1E就是AC1与平面BB1C1C所成的角，
不妨设正三棱柱ABC﹣A1B1C1的所有棱长都为2，则C1E＝，AC1＝2
在Rt△AC1E中，cs∠AC1E＝＝
故答案为：
三．解答题
16．【考点】直线与平面所成的角；直线与平面平行．
【解答】（1）证明：设AD交BC于点F，
∵O为△ABC外心，
又∵．
又OA＝OD＝r＝＝2，∴F为OD中点．
∴△POD中E，F分别为PD，OD中点，
∴EF∥PO（中位线定理），
∵EF∥PO，EF⊂平面ECB，
∴直线PO∥平面BCE．
（2）解：∵AE⊥PD，E为PD中点，又PA＝PD，∴△APD为等边三角形．
过O作OQ⊥AD且OQ⊂平面ABC，Q位于上，
以O为空间坐标原点，，，为x轴，y轴，z轴正向建立空间直角坐标系．
则：A（0，﹣2，0），，＝（0，2，2），
B（，1，0），E（0，1，），
＝（，3，0），＝（﹣，0，）．
设平面ABE的法向量为，
，∴，
取，则y＝﹣1，．
则，
设直线AP与平面ABE所成角的正弦值为sinθ，
，
∴直线AP与平面ABE所成角正弦值为．
17．【考点】直线与平面所成的角；直线与平面平行．
【解答】（Ⅰ）证明：方法1：设G为DE的中点，连接FG，AG，
由已知CF∥DE，且CF＝DG，
所以四边形CFGD是平行四边形，…………（1分）
又ABCD为正方形，
所以ABFG为平行四边形，…………（2分）
所以BF∥AG，…………（3分）
又AG⊂平面ADE，BF⊄平面ADE，…………（4分）
所以BF∥平面ADE．…………（5分）
方法2：因为CF∥DE，所以CF∥平面ADE，
又CB∥DA，所以CB∥平面ADE，CB∩CF＝C，
所以平面BCF∥平面ADE，
所以BF∥平面ADE．
（Ⅱ）解：因为ABCD为正方形，DE⊥平面ABCD，
以D为坐标原点建立空间直角坐标系（如图）…………（1分）
所以 A（2，0，0），E（0，0，2），F（0，2，1），B（2，2，0），…………（2分）
，，，…………（3分）
设平面AEF的一个法向量为＝（x，y，z），
则…………（4分）
即
令z＝2，得x＝2，y＝1．
于是＝（2，1，2）．…………（5分）
设直线BD与平面AEF所成角为θ，则，…………（7分）
即，…………（8分）
所以直线BD与平面AEF所成的角为．…………（9分）
18．【考点】直线与平面所成的角；点、线、面间的距离计算．
【解答】解：（1）证明：连接BD，则O是BD的中点，且AC⊥BD，
在正四棱锥P﹣ABCD中，PO⊥平面ABCD，
以点O为坐标原点，OA，OB，OP所成直线分别为x，y，z轴，建立空间直角坐标系，如图，
则O（0，0，0），A（3，0，0），P（0，0，3），B（0，3，0），C（﹣3，0，0），D（0，﹣3，0），M（0，0，），E（0，2，1），
＝（0，3，），，
则，取y＝1，得＝（0，1，﹣2），
∵＝0，∴，
∵DM⊄平面EAC，∴DM∥平面EAC．
（2）（i）＝（3，3，0），
∴直线DM到平面EAC的距离d＝＝＝．
（ii）＝（3，0，﹣），
则cs＜＞＝＝＝．
∴直线MA与平面EAC所成角的正弦值为．