人教版七年级下册5.4 平移测试题

这是一份人教版七年级下册5.4 平移测试题，共7页。试卷主要包含了在下列实例中，属于平移过程的有，下列运动属于平移的是，下列现象中，属于平移的是等内容，欢迎下载使用。
1．在下列实例中，属于平移过程的有（ ）
①时针运行的过程；
②电梯上升的过程；
③地球自转的过程；
④小汽车在平直的公路行驶．
A．1个B．2个C．3个D．4个
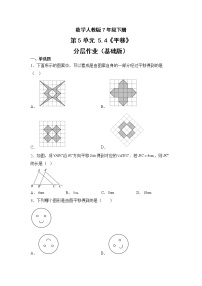
2．下面四个选项中的图形，可以从所给的心形图平移得到的是（ ）
A．B．C．D．
3．下列运动属于平移的是（ ）
A． 荡秋千
B． 钟摆的摆动
C．随风摆动的五星红旗
D．在笔直公路上行驶的汽车
4．下列现象中，属于平移的是（ ）
A．滚动的足球B．转动的电风扇叶片
C．正在上升的电梯D．正在行驶的汽车后轮
二．填空题（共3小题）
5．如图，△ABC沿AB平移后得到△DEF，点D是点A的对应点．如果AE＝10，BD＝2，那么△ABC平移的距离是 ．
6．如图，将△ABC沿射线BC平移3个单位后得到△DEF，连接AD，若AD＝3EC，则BF的长为
7．如图，△ABC沿BC方向平移得到△DEF．若BF＝13，EF＝9，则EC的长是 ．
三．解答题（共3小题）
8．如图，将△ABC沿BC方向平移得到△DEF，△ABC与△DEF重叠部分（图中阴影部分）的面积是△ABC的一半．已知BC＝2，求△ABC平移的距离．
9．如图，方格纸中每个小正方形的边长都为1，△ABC的顶点都在方格纸的格点上，将△ABC经过平移，使点C移到点C′的位置．
（1）画出△A′B′C′；
（2）连接AA′、BB′，这两条线段的关系是 ；
（3）△B′CC′的面积为 ．
10．如图，在平面直角坐标系xOy中，三角形ABC三个顶点的坐标分别是A（4，2），B（1，0），C（5，﹣3），三角形ABC中任意一点P（x0，y0），经平移后对应点为P′（x0﹣6，y0+2），将三角形ABC作同样的平移得到三角形A'B'C'，点A，B，C的对应点分别为A′，B′，C′．
（1）点A′的坐标为 ，点B′的坐标为 ；
（2）①画出三角形A′B′C′；
②写出三角形A′B′C′的面积；
（3）过点A′作A′D∥y轴，交B′C′于点D，则点D的坐标为 ．
（基础篇）2023-2024学年下学期初中数学人教版七年级同步分层作业5.4平移
参考答案与试题解析
一．选择题（共4小题）
1．在下列实例中，属于平移过程的有（ ）
①时针运行的过程；
②电梯上升的过程；
③地球自转的过程；
④小汽车在平直的公路行驶．
A．1个B．2个C．3个D．4个
【分析】根据平移的定义直接判断即可．
【解答】解：①时针运行的过程是旋转；
②电梯上升的过程是平移；
③地球自转的过程是旋转现象；
④小汽车在平直的公路行驶是平移．
故属于平移的有2个．
故选：B．
【点评】本题考查了生活中的平移现象，图形的平移只改变图形的位置，而不改变图形的形状和大小，学生易混淆图形的平移与旋转或翻转而误选．
2．下面四个选项中的图形，可以从所给的心形图平移得到的是（ ）
A．B．C．D．
【分析】根据平移的性质即可判断．
【解答】解：根据平移的性质可知图形可以从所给的心形图平移得到，
故选：C．
【点评】本题考查了平移的性质，熟练掌握平移前后图形的形状大小不变是解题的关键．
3．下列运动属于平移的是（ ）
A． 荡秋千
B． 钟摆的摆动
C．随风摆动的五星红旗
D．在笔直公路上行驶的汽车
【分析】在平面内，把一个图形整体沿某一直线的方向移动，这种图形的平行移动，叫做平移变换，简称平移．根据平移的概念进而得出答案．
【解答】解：A、荡秋千，属于旋转变换，不符合题意；
B、钟摆的摆动，属于旋转变换，不符合题意；
C、随风摆动的五星红旗，不属于平移变换，不符合题意；
D、在笔直公路上行驶的汽车，属于平移，符合题意；
故选：D．
【点评】本题考查了生活中的平移现象，熟练掌握平移的定义是解题的关键．
4．下列现象中，属于平移的是（ ）
A．滚动的足球B．转动的电风扇叶片
C．正在上升的电梯D．正在行驶的汽车后轮
【分析】利用平移的定义进行判断即可．
【解答】解：A．滚动的足球是旋转，
故不符合题意；
B．转动的电风扇叶片是旋转，
故不符合题意；
C．正在上升的电梯是平移，
故符合题意；
D．正在行驶的汽车后轮是旋转，
故不符合题意；
故选：C．
【点评】本题考查平移的定义，掌握图形经过平移，对应线段相等，对应角相等，对应点所连的线段相等是解题的关键．
二．填空题（共3小题）
5．如图，△ABC沿AB平移后得到△DEF，点D是点A的对应点．如果AE＝10，BD＝2，那么△ABC平移的距离是 4 ．
【分析】直接利用平移的性质得出方程进而得出答案．
【解答】解：设平移的距离为x，则EB＝AD＝x，
则BE+BD+AD＝10，
故x+2+x＝10，
解得：x＝4，
即△ABC平移的距离是：4．
故答案为：4．
【点评】此题主要考查了平移的性质，正确得出等式是解题关键．
6．如图，将△ABC沿射线BC平移3个单位后得到△DEF，连接AD，若AD＝3EC，则BF的长为 7
【分析】利用平移的性质得到AD＝BE＝CF＝3，由AD＝3EC可求BC，根据线段的和差求出BF即可．
【解答】解：∵△ABC沿射线BC平移3个单位得到△DEF，
∴AD＝BE＝CF＝3，
∵AD＝3EC，
∴EC＝1，
∴BF＝BE+CE+CF＝3+1+3＝7，
故答案为：7．
【点评】本题考查了平移的性质：新图形中的每一点，都是由原图形中的某一点移动后得到的，这两个点是对应点．连接各组对应点的线段平行（或共线）且相等．
7．如图，△ABC沿BC方向平移得到△DEF．若BF＝13，EF＝9，则EC的长是 5 ．
【分析】根据△ABC沿BC方向平移得到△DEF求出BC，从而可求出BE，即可求得EC．
【解答】解：∵△ABC沿BC方向平移得到△DEF，
∴BC＝EF＝9，
∵BF＝13，
∴BE＝BF﹣EF＝13﹣9＝4，
∴EC＝BC﹣BE＝9﹣4＝5，
故答案为：5．
【点评】本题考查平移的性质，解题的关键是根据平移的性质求出BC＝EF＝9．
三．解答题（共3小题）
8．如图，将△ABC沿BC方向平移得到△DEF，△ABC与△DEF重叠部分（图中阴影部分）的面积是△ABC的一半．已知BC＝2，求△ABC平移的距离．
【分析】移动的距离可以视为FC或BE的长度，根据题意可知△ABC与阴影部分为相似三角形，且面积比为2：1，所以BC：EC=2：1，推出EC=2，所以BE＝2-2．
【解答】解：∵△ABC沿BC边平移到△DEF的位置，
∴AB∥EG，
∴△ABC∽△GEC，
∴S阴影S△ABC=（CEBC）2=12，
∴BC：EC=2：1，
∵BC＝2，
∴EC=2，
∴△ABC平移的距离为：BE＝2-2．
【点评】本题主要考查相似三角形的判定和性质、平移的性质，关键在于求证△ABC与阴影部分为相似三角形．
9．如图，方格纸中每个小正方形的边长都为1，△ABC的顶点都在方格纸的格点上，将△ABC经过平移，使点C移到点C′的位置．
（1）画出△A′B′C′；
（2）连接AA′、BB′，这两条线段的关系是 AA′∥BB′且AA′＝BB′ ；
（3）△B′CC′的面积为 5 ．
【分析】（1）利用C点和C′点的位置确定平移的方向与距离，然后根据此平移规律确定A′、B′的位置；
（2）根据平移的性质进行判断；
（3）利用割补法进行计算．
【解答】解：（1）△A′B′C′即为所求；
（2）AA′∥BB′且AA′＝BB′．
故答案为：AA′∥BB′且AA′＝BB′；
（3）S△B′CC′=3×4-12×3×1-12×3×1-12×2×4=5．
故答案为：5．
【点评】本题考查了作图﹣平移变换：作图时要先找到图形的关键点，分别把这几个关键点按照平移的方向和距离确定对应点后，再顺次连接对应点即可得到平移后的图形．
10．如图，在平面直角坐标系xOy中，三角形ABC三个顶点的坐标分别是A（4，2），B（1，0），C（5，﹣3），三角形ABC中任意一点P（x0，y0），经平移后对应点为P′（x0﹣6，y0+2），将三角形ABC作同样的平移得到三角形A'B'C'，点A，B，C的对应点分别为A′，B′，C′．
（1）点A′的坐标为 （﹣2，4） ，点B′的坐标为 （﹣5，2） ；
（2）①画出三角形A′B′C′；
②写出三角形A′B′C′的面积；
（3）过点A′作A′D∥y轴，交B′C′于点D，则点D的坐标为 （﹣2，-14） ．
【分析】（1）由点P的对应点P′坐标知，需将三角形向左平移6个单位、向上平移2个单位，据此可得；
（2）①根据平移规律求出C′点的坐标，根据A′，B′，C′点的坐标即可画出三角形A′B′C′；
②利用割补法求解可得答案；
（3）设D（﹣2，m），利用面积法求解．
【解答】解：（1）点A′的坐标为（4﹣6，2+2），点B′的坐标为（1﹣6，0+2），即A（﹣2，4），B（﹣5，2）；
故答案为：（﹣2，4），（﹣5，2）；
（2）①如图，△A′B′C′即为所求；
②△A′B′C′的面积＝5×4-12×5×1-12×2×3-12×3×4=172；
（3）设D（﹣2，m），则有172=12×（4﹣m）×4，
解得m=-14，
∴D（﹣2，-14），
故答案为：（﹣2，-14）．
【点评】此题主要考查了平移作图，关键是正确确定组成图形的关键点平移后的位置．