

河南省名校联盟2024届高三下学期4月教学质量检测数学试卷(Word版附解析)
展开注意事项:
1.答卷前,考生务必将自己的姓名、考生号、考场号和座位号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上。写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.若 a+2i2-3i为纯虚数,a∈R,则a=
A.3 B.4 C.-3 D.-4
2.设集合A={1,-a},B={0,3-a,3a-8},若A⊆B,则a=
A.0 B.1 C.2 D.3
3.已知圆锥的底面圆的半径为1,其侧面展开图是一个圆心角为π/2的扇形,则该圆锥的母线长为
A. 52 B.3 C. 72 D.4
4.已知函数 fx=2sin2x-π3cs2x+π3,则下列结论正确的是
A. f(x)的最小正周期为π B. f(x)在( -π8π4上单调递增
C. f'(x)为偶函数 D. f(x)的最小值为 32
5.已知点 P(m,n)是圆 C :x²+y²=8上的任意一点,则( m-n214m+n2+1的最大值为
A.25 B.24 C.23 D.22
6.过双曲线 C.x24-y2=1的左焦点 F₁ 作倾斜角为θ的直线l交C于M,N两点,若 MF1=3F1N,则|csθ|=
A.1010 B.31010 C.255 D.55
7.将8个数学竞赛名额全部分给4个不同的班,其中甲、乙两班至少各有1个名额,则不同的分配方案种数为
A.56 B.84 C.126 D.210
8.已知函数f(x)的定义域为R,对于任意实数x,y满足f(x+y)+f(x-y)=2f(x+1)f(y),且 f(0)=2,则下列结论错误的是
A. f(1)=1 B. f(x)为偶函数
C. f(x)是周期函数 D.f10=1512
二、选择题:本题共 3小题,每小题6分,共 18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
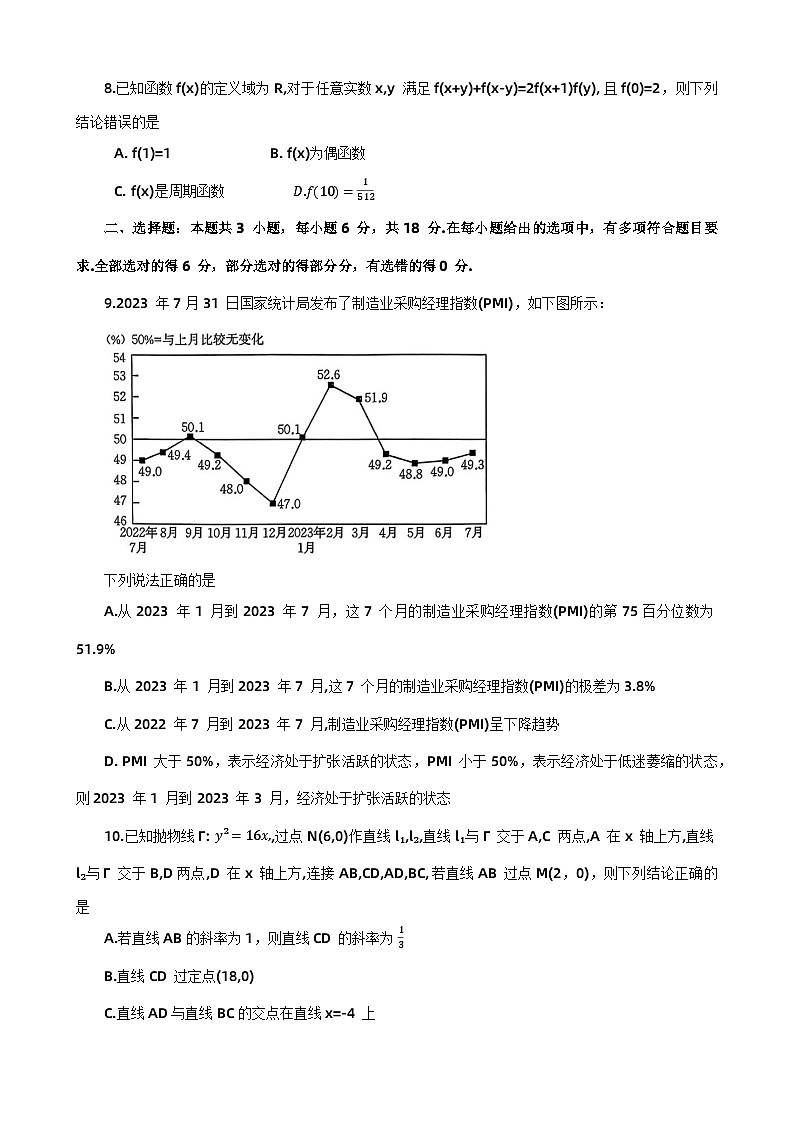
9.2023年7 月 31日国家统计局发布了制造业采购经理指数(PMI),如下图所示:
下列说法正确的是
A.从2023年1月到 2023年7月,这7个月的制造业采购经理指数(PMI)的第75 百分位数为51.9%
B.从 2023年1月到2023年7月,这7个月的制造业采购经理指数(PMI)的极差为3.8%
C.从 2022年7月到 2023年7月,制造业采购经理指数(PMI)呈下降趋势
D. PMI大于50%,表示经济处于扩张活跃的状态,PMI小于50%,表示经济处于低迷萎缩的状态,则2023年1月到 2023年3月,经济处于扩张活跃的状态
10.已知抛物线Γ: y²=16x,,过点 N(6,0)作直线l₁,l₂,直线l₁与Γ交于A,C两点,A在x轴上方,直线l₂与Γ交于B,D 两点,D在x轴上方,连接AB,CD,AD,BC,若直线AB过点M(2,0),则下列结论正确的是
A.若直线AB 的斜率为1,则直线CD的斜率为 13
B.直线CD过定点(18,0)
C.直线AD 与直线BC 的交点在直线x=-4上
D.△ABN 与△CDN的面积之和的最小值为 1602
11.已知定义在R上的奇函数 f(x)连续,函数f(x)的导函数为f'(x).当x>0时,.f'(x) csx >fxsinx+e⋅f'x,,其中e为自然对数的底数,则
A. f(x)在R上为减函数
B.当x>0时,f(x)<0
C.fπ2>f3π2
D.∫(x)在 R上有且只有1个零点
三、填空题:本题共3小题,每小题5分,共15分.
12.已知数列{an}的前n项和为Sn,若( aₙ=λn+1,a₁₀=21,则 λ=.
13.太极图被称为“中华第一图”,其形状如阴阳两鱼互抱在一起,因而又被称为“阴阳鱼太极图”.如图所示的图形是由半径为2 的大圆O和两个对称的半圆弧组成的,线段MN过点O 且两端点M,N 分别在两个半圆弧上,点P 是大圆上一动点,则 PM⋅PN的最小值为 ▲ .
14.已知正四棱台. ABCD-A₁B₁C₁D₁的内切球半径 r=22,AB=2A1B1,则异面直线 A₁B₁与 DD₁所成角的余弦值为 ▲ .
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)
在△ABC中,内角A,B,C的对边分别为a, b,c, a=2,55sinA=1-csA.
(1)求 cs A;
(2)若AD为△ABC的中线,且. AD=3,,求△ABC的面积S.
16.(15分)
如图,在四棱锥 P-ABCD 中,底面 ABCD 为平行四边形,且 ∠ABC=π3,,平面 PAC⊥平面AB-CD. F为PA的中点,且CF=PF,PC=4,BC=2,PB=PD,M,N分别为PB,PD的中点.
(1)证明:BD⊥AC.
(2)设DM交平面 NAC于点 H,求平面ABC与平面ABH夹角的余弦值.
17.(15分)
某市共有教师1000名,为了解老师们的寒假研修情况,评选研修先进个人,现随机抽取了10名教师利用“学习 APP”学习的时长(单位:小时):35,43,90,83,50,45,82,75,62,35.时长不低于 80 小时的教师评为“研修先进个人”.
(1)现从该样本中随机抽取3名教师的学习时长,求这3名教师中恰有2名教师是研修先进个人的概率.
(2)若该市所有教师的学习时长 X 近似地服从正态分布 Nμσ²,其中 σ=10,μ为抽取的 10名教师学习时长的样本平均数,利用所得正态分布模型解决以下问题:
①试估计学习时长不低于50小时的教师的人数(结果四舍五入到整数);
②若从该市随机抽取的n名教师中恰有ξ名教师的学习时长在[50,70]内,则n为何值时,P(ξ=10)的值最大?
附:若随机变量 X 服从正态分布N(μ,σ²),则.P(μ-σ≤X≤μ+σ)≈0.6827,P(μ--2σ≤X≤μ+2σ)≈0.9545,P(μ-3σ≤X≤μ+3σ)≈0.9973.
18.(17分)
如图所示,在圆锥内放入两个球O₁,O₂,它们都与圆锥的侧面相切(即与圆锥的每条母线相切),且这两个球都与平面α相切,切点分别为 F₁,F₂,数学家丹德林利用这个模型证明了平面α与圆锥侧面的交线为椭圆,记为Γ,F₁,F₂为椭圆Γ的两个焦点.设直线 F₁F₂分别与该圆锥的母线交于A,B两点,过点A的母线分别与球O₁,O₂相切于 C,D 两点,已知|AC|= 2-3,|AD|=2+3.以直线 F₁F₂为x轴,在平面α内,以线段 F₁F₂的中垂线为y轴,建立平面直角坐标系.
(1)求椭圆Γ的标准方程.
(2)点 T在直线x=4上,过点T作椭圆Γ的两条切线,切点分别为M,N,A,B分别是椭圆Γ的左、右顶点,连接AM,BN,设直线AM与BN交于点P.证明:点 P 在直线x=4上.
19.(17分)
已知b>0,函数 f(x)=(x+a) ln(x+b)的图象在点(1,f(1))处的切线方程为xln 2-y-ln 2=0.
(1)求a,b的值;
(2)若方程 fx=1e(e为自然对数的底数)有两个实数根x₁,x₂,且. x₁
1. A 【解析】本题考查复数的运算,考查数学运算的核心素养.
因为 a+2i2-3i=a+2i2+3i13=2a-6+3a+4i13为纯虚数,所以2a-6=0,解得a=3.
2. C 【解析】本题考查集合的基本运算,考查数学运算的核心素养.
因为A⊆B,所以-a=0或-a=3a-8,解得a=0或a=2.当a=0时,A={1,0},B={0,3,-8},不符合题意.当a=2时,A={1,-2},B={0,1,-2},符合题意.故选 C.
3. D 【解析】本题考查圆锥的侧面展开图,考查直观想象的核心素养.
设母线长为l,由 π2l=2π×1,得l=4.
4. C 【解析】本题考查三角函数的图象与性质,考查直观想象、数学运算的核心素养.
因为 fx=2sin2x-π3cs2x+π3=sin4x-32.所以 A错误,D错误.因为 -π8
由已知,设 m=22csα,n=22sinα,则 m-n)214m+n2+1=8csα-sinα2[2csα+sinα2+ ]=81-sin2α3+2sin2α≤42-2sin2α+3+2sin2α22=25 当且仅当 sin2α=-14时,等号成立.
6. D 【解析】本题考查双曲线的性质,考查数学运算的核心素养.
由焦比定理可得 |ecsθ|=|3-13+1|=12,又 e=52, 所以 |csθ|=55.
7. B 【解析】本题考查用排列组合解决实际问题,考查数学建模的核心素养和应用意识.
将8个数学竞赛名额全部分给4个不同的班,其中甲、乙两班至少各有1个名额的分法,等价于将 10个数学竞赛名额全部分给4个不同的班,每个班至少有1个名额的分法.用3个隔板插入10个小球中间的空隙中,将球分成4堆,由于 10个小球中间共有 9个空隙,因此共有 C93=84种不同的分法.
8. C 【解析】本题考查抽象函数的性质,考查数学抽象、逻辑推理的核心素养.
令x=y=0,得2f(0)=2f(1)f(0),因为f(0)=2,所以 f(1)=1,A正确;
令x=0,则.f(y)+f(-y)=2f(1)f(y)=2f(y),月所以f(y)=f(-y),则f(x)为偶函数,B正确;
令y=0,得2f(x)=2f(x+1)f(0)=4f(x+1),即 fx+1=12fx,所以 f(x)不是周期函数,C错误;
当x取正整数n时, fn+1=12fn=12nf1=12n,则 f10=129=1512,D.正确.
9. ABD 【解析】本题考查统计的知识,考查数据分析的核心素养和应用意识.
由图知,从2023年1月到 2023 年7月,这7个月的制造业采购经理指数(PMI)从小到大的顺序为 48.8%,49.0%,49.2%,49.3%,50.1%,51.9%,52.6%,因为7×75%=5.25,所以第75 百分位数为第6个数,即为51.9%,故A 正确;从2023年1月到2023年7月,这7个月的制造业采购经理指数(PMI)的最大值为 52.6%,最小值为48.8%,所以极差为52.6%-48.8%=3.8%,故B正确;由图易知C错误,D正确.
10. ABD 【解析】本题考查抛物线的性质,考查直观想象的核心素养.
设A(x₁,y₁),B(x₂,y₂),C(x₃,y₃),D(x₄,y₄),设直线 CD交x轴于点(t,0),联立方程组 y1y2=-32,y1y3=-96,92y4=-96,3y4=-16t,可得t=18,B正确 kABkCD2yy1+y22py3+y4y1+y2=-96y1-96y2y1+y2=-96y1y2=-96-32=3,当 kAB=1时, k(D=13,A正确;当l₁⊥x轴时,可知 A646,C6-46,D54126, B23-463,求得直线 AD的方程为 x=6y-18,,直线 BC的方程为 6x+2y+26=0,将这两方程联立方程组,解得x=-6,C错误;设△ABN 与△CDN的面积分别为S₁,S₂,则 S1+S2=12×6-2×y1-y2+12×18-6×y4-y3=2y1-y2+6y4-y3又 y1-y2=y1+32y1≥82,y4-y3=y4+16×18y4≥242,所以 S1+S2≥1602,当且仅当 y₁= 42,y4=122时,等号成立,D正确.
11. BCD 【解析】本题考查导数在研究函数中的应用,考查逻辑推理的核心素养.
由f'(x) csx>f(x) sinx+e·f'(x),得.f'(x)(csx-e)-f(x) sinx>0.
令 g(x)=f(x)(csx--e),则当x>0时, g'x=f'xcsx-e-fxsinx>0,所以g(x)在(0,+∞)上单调递增,所以 gπ2
因为g(0)=f(0)(1-e)=0,所以当x>0时,g(x)>g(0)=0.又因为 csx-e<0,所以当x>0时,f(x)<0,B正确.
由于 f(x)是定义在R上的奇函数,故当x<0时,f(x)=--f(-x)>0.
又 f(0)=0,所以 f(x)在R上有且只有1个零点,D正确.
因为 f(x)的单调性无法判断,所以 A 错误.
12.2;99 【解析】本题考查等差数列的求和,考查数学运算的核心素养.
由10λ+1=21,得λ=2.因为 aₙ=2n+1,所以{an}是等差数列,则 S₉=9a₅=9×11=99.
13.0 【解析】本题考查平面向量的数量积,考查直观想象、数学运算的核心素养.
连接 PO,可得 PM⋅PN=PO+OM⋅PO-OM=PO2-OM2=4- OM2,显然当 OM2最大,即 |OM|取得最大值2时, PM⋅PN取得最小值0.
14.1010 【解析】本题考查四棱锥的内切球、异面直线所成的角,考查直观想象、数学运算的核心素养.
由题设知正四棱台 ABCD-A₁B₁C₁D₁的高 h=2.设 AB=2A₁B₁=4a,作正四棱台的轴截面,如图所示,其中I,J,L 分别为圆O与四边形 EFGH 的切点,FK⊥GH,K 为垂足,则 IF=FL=a,JG=GL=2a,所以, KG=a,FK=2,FG=3a,由 9a²-a²= 22,解得 a=12.延长侧棱 DD₁,CC₁,设它们相交于点 P,则异面直线A₁B₁与 DD₁所成的角为∠PD₁C₁.因为 PG=6a=3,12CD=1,所以 PC=PD=32+12=10,从而 cs∠PD1C1=110=1010.
15.解:(1)由 55sinA=1-csA,得 255sinA2csA2=2sin2A2, 2分
又0
所以 csA=2cs2A2-1=23. 6分
(2)由(1)知 sinA=53, 7分
因为 AD为△ABC 的中线, AD=3,所以 AB+AC=2AD, 9分
两边平方得 b2+c2+43bc=12. …… 10分
又 b²+c²-2bccsA=4,即 b2+c2-43bc=4, …11分
两式相减,得bc=3, · …12分
所以 S=12bcsinA=12×3×53=52. …13分
16.(1)证明:如图1,设 BD与AC 交于点O,连接 PO.
因为底面ABCD是平行四边形,所以O为BD,AC的中点.
因为PB=PD,所以PO⊥BD.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯2分
又CF=FP=FA,所以PC⊥AC.…………………………………………………………4分
因为 PC⊂平面 PAC,且平面 PAC⊥平面 ABCD,平面 PAC∩平面ABCD=AC,所以 PC⊥平面 ABCD.
因为BD⊂平面ABCD,所以PC⊥BD.……………………………5分
因为 PO∩PC=P,所以 BD⊥平面 PAC.
因为AC⊂平面PAC,所以BD⊥AC.………………………………7分
(2)解:连接ON,因为ON为△PBD的中位线,所以ON∥PB.
因为平面 PBD∩平面ACH=OH,BM=ON且H∈ON,所以OH∥MB,且 OH=12MB.易证OF⊥平面ABCD.…………………………………9分
以OA,OB,OF 所在直线分别为x,y,z轴,建立如图2所示的空间直角坐标系,则O(0,0,0),F(0,0,2),A(1,0,0),C(--1,0,0),B(0, 3,0),P(-1,0,4),所以 OH=14BP=-14-341. ……………11分
设m=(x,y,z)为平面ABH的法向量,因为 AB=-130,AH=
-54-341,所以 m⋅AB=-x+3y=0,m⋅AH=-5x4-3y4+z=0.令 y=2,得m=
23233.…………………………………13分
平面ABC的一个法向量为n=(0,0,1).………………………………………………14分
设平面 ABC 与平面ABH 的夹角为θ,
所以 csθ=|m⋅n|m|⋅|n||=334+12+27=312943.…15分
17.解:(1)设事件“抽取的3名教师中恰有2名教师是研修先进个人”为A.
由题知样本中学习时长不低于 80 小时的人数为3,时长低于 80 小时的人数为7,…… 2分
则 PA=C32C71C103=740,,即这3名教师中恰有 2 名教师是研修先进个人的概率为 740.…4分
(2)①由样本数据知, μ=35+43+⋯+3510=60,σ=10.⋯5分
因为 CX≥50=PX≥μ-σ=Pμ-σ≤X≤μ+σ2+12≈0.84135,…7分
所以0.84135×1000≈841,即学习时长不低于50小时的教师人数为841.⋯⋯⋯⋯⋯8分
②每名教师的学习时长在[50,70]内的概率为P(μ-σ≤X≤μ+σ)≈0.6827,………10分
由题意可知ξ~B(n,0.6827),则 Pξ=10=Cn10×0.682710×0.3173n-10,…11分
设 fn=Cn10×0.682710×0.3173n-10n≥10,则 fn+1fn=Cn+110×0.682710×0.3173n-9Cn10×0.682710×0.3173n-10=
… ……………………………………………………………………………13分
令得 n<931736827=1344226827,所以当n≤13时,f(n+1)>f(n),
令得 n>1344226827,所以当n≥14时,f(n+1)
18.(1)解:设椭圆Γ的标准方程为 x2a2+y2b2=1ab>0),
由切线长定理知| |AF₁|=|AC|,|AF₂|=|AD|,……2分
则| |AF₁|+|AF₂|=|AC|+|AD|=2a=4,解得a=2.⋯4分
由 |AD|-|AC|=23=2c,解得 c=3,b=1.…6分
所以椭圆Γ的标准方程为 x24+y2=1.………………7分
(2)证明:设P(x₀,y₀),M(x₁,y₁),N(x₂,y₂),T(4,t),已知A(-2,0),B(2,0).设PA:y=k₁(x+2),PB:y=k₂(x-2).…………………………………………………8分
联立方程组 x24+y2=1,y=k1x+2,消去 y得( 1+4k12x2+16k12x+16k12-4=0,
由 -2x1=16k12-41+4k12, 可得 x1=2-8k121+4k12, …9分
所以 M2-8k121+4k124k11+4k12, 同理 N8k22-21+4k22-4k21+4k22. … 11分
因为 M,N是切点,且T(4,t),所以直线MN的方程为 4x4+ty=1,即x+ty=1,…… 13分
显然直线MN过定点D(1,0),即M,D,N三点共线,则 4k11+4k122-8k121+4k12-1-4k21+4k221+4k22-1,
解得 k₂=3k₁或 4k₁k₂=-1(舍去),………………………………………16分
联立方程组 y0=k1x0+2,y0=k2x0-2,解得 x0=2k1+k2k2-k1=4,即点 P 在直线x=4上. … 17分
19.(1)解:因为 f'x=x+ax+b+lnx+b,所以 f'1=1+a1+b+ln1+b=ln2.…3分
由题意知f(1)=0,所以f(1)=(1+a)ln(b+1)=0.……………………………………4分
联立方程组 1+alnb+1=0,1+a1+b+ln1+b=ln2,解得a=-1,b=1.…6分
(2)证明:由(1)可知f(x)=(x-1) ln(x+1),x>--1,f(0)=0,f(1)=0, f'x=1-2x+1+lnx+1,易知f'(x)在(-1,+∞)上单调递增.…………………7分
又f'(0)=-1<0,f'(1)=ln 2>0,所以存在x₀∈(0,1),使得. f'x₀=0,
故f(x)在(-1,x₀)上单调递减,在(x₀,+∞)上单调递增.……………………………8分
设h(x)=(x--1)·ln 2,令.F(x)=f(x)-h(x)=(x--1) ln(x+1)--(x--1)·ln 2,则
F'x=x-1x+1+lnx+1-ln2=lnx+1-2x+1+1-ln2,易知F'(x)在(-1,+∞)上单调递增.……………………………………………………………………………………10分
又 F'(1)=0,所以当x∈(-1,1)时,, F'x<0,,当x∈(1,+∞)时,F'(x)>0.
所以F(x)在(-1,1)上单调递减,在(1,+∞)上单调递增.
故 F(x)≥F(1)=0,即(x-1) ln(x+1)≥(x-1) ln 2,当且仅当x=1时,等号成立. …………………………………………………………11分
易知 x₂>1,所以( x₂-1lnx₂+1>x₂-1ln2,即 fx₂>hx₂.…12分
设 hx=1e的根为:x₂',则 x2'=1+1eln2.
又h(x)在(--1,+∞)上单调递增,所以 hx₂'=fx₂>hx₂,故x₂'>x₂①. ………13分易知f(x)的图象在坐标原点处的切线方程为g(x)=-x,
令T(x)=f(x)-g(x)=(x-1) ln(x+1)+x,
则 T'x=2xx+1+lnx+1=2-2x+1+lnx+1,易知T'(x)在(--1,+∞)上单调递增.…………………………………………14分
又 T'0=0,,所以当x∈(-1,0)时, T'x<0,,当x∈(0,+∞)时,T'(x)>0,
所以T(x)在(-1,0)上单调递减,在(0,+∞)上单调递增.
所以T(x)≥T(0)=0,(x--1) ln(x+1)≥-x,当且仅当x=0时,等号成立.因为 x₁<0,所以 x₁-1lnx₁+1>-x₁,即 fx₁>gx₁.……………………………………………15分
设 gx=1e的根为x₁',则 x1'=-1e.
又g(x)在(--1,+∞)上单调递减,所以 gx₁'=fx₁>gx₁,所以 x₁'
由①②可知 x2-x1
河南省名校联盟2023-2024学年高三下学期教学质量检测(3月)数学试卷(原卷版+解析版): 这是一份河南省名校联盟2023-2024学年高三下学期教学质量检测(3月)数学试卷(原卷版+解析版),文件包含河南省名校联盟2023-2024学年高三下学期教学质量检测3月数学试卷原卷版docx、河南省名校联盟2023-2024学年高三下学期教学质量检测3月数学试卷解析版docx等2份试卷配套教学资源,其中试卷共26页, 欢迎下载使用。
河南省名校联盟2023-2024学年高三下学期3月教学质量检测试题 数学 Word版含解析: 这是一份河南省名校联盟2023-2024学年高三下学期3月教学质量检测试题 数学 Word版含解析,共13页。试卷主要包含了给出下列四个命题,下列说法正确的是,65x+3等内容,欢迎下载使用。
河南省名校联盟2023-2024学年高三下学期3月教学质量检测数学试题(Word版附解析): 这是一份河南省名校联盟2023-2024学年高三下学期3月教学质量检测数学试题(Word版附解析),共13页。试卷主要包含了给出下列四个命题,下列说法正确的是,65x+3等内容,欢迎下载使用。












