2024年湖南省湘潭市中考一模数学试题

这是一份2024年湖南省湘潭市中考一模数学试题，共13页。试卷主要包含了下列事件中，是必然事件的是等内容，欢迎下载使用。

数学
本试卷共8页．全卷满分120分，考试时间120分钟．
注意事项：
1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上．
2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号，回答非选择题时，将答案写在答题卡上，写在本试卷上无效．
3．考试结束后，将本试卷和答题卡一并交回．
一、选择题（本大题共10个小题，每小题有且只有一个正确答案，请将正确答案的选项代号涂在答题卡相应的位置上，每小题3分，满分30分）
1．下列四个数中最小的数是（ ）
A．B．3.14C．0D．
2．下列汽车图标既不是轴对称图形，也不是中心对称图形的是（ ）
A．B．C．D．
3．下列计算正确的是（ ）
A．B．C．D．
4．菲尔兹奖是数学领域的一项国际大奖，被视为数学界的诺贝尔奖，其规定获奖数学家年龄不得超过40岁．截至目前，菲尔兹奖得主中最年轻的8位数学家获奖时年龄分别为：29，27，31，31，31，29，29，31，则该组由年龄组成的数据的众数和中位数分别是（ ）
A．29，31B．29，29C．31，30D．30，31
5．已知一元二次方程有一个根是，则的值是（ ）
A．2B．C．1D．
6．下列事件中，是必然事件的是（ ）
A．守株待兔B．水中摸月
C．三角形三边之长为D．若，则
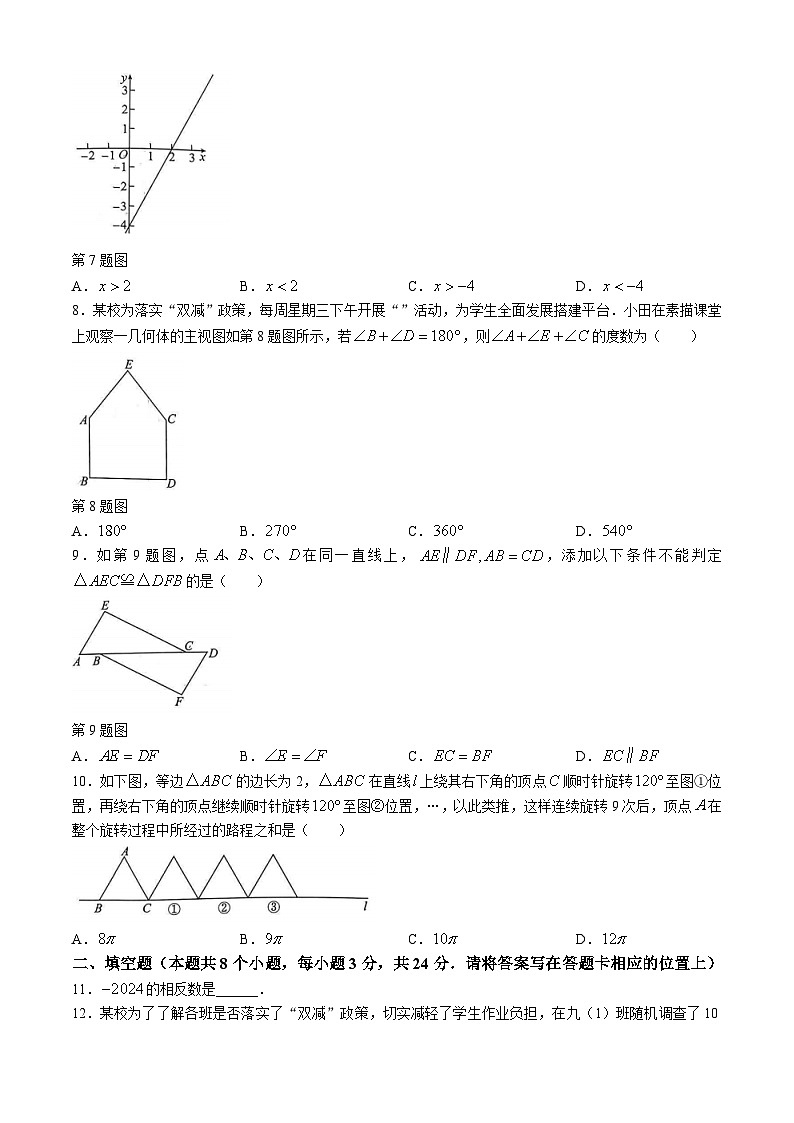
7．如第7题图，一次函数的图象经过点，当时，的取值范围是（ ）
第7题图
A．B．C．D．
8．某校为落实“双减”政策，每周星期三下午开展“”活动，为学生全面发展搭建平台．小田在素描课堂上观察一几何体的主视图如第8题图所示，若，则的度数为（ ）
第8题图
A．B．C．D．
9．如第9题图，点在同一直线上，，添加以下条件不能判定的是（ ）
第9题图
A．B．C．D．
10．如下图，等边的边长为2，在直线上绕其右下角的顶点顺时针旋转至图①位置，再绕右下角的顶点继续顺时针旋转至图②位置，…，以此类推，这样连续旋转9次后，顶点在整个旋转过程中所经过的路程之和是（ ）
A．B．C．D．
二、填空题（本题共8个小题，每小题3分，共24分．请将答案写在答题卡相应的位置上）
11．的相反数是______．
12．某校为了了解各班是否落实了“双减”政策，切实减轻了学生作业负担，在九（1）班随机调查了10名学生每天完成作业的时长，调查数据统计如下表：
请你估计九（1）班学生每天完成作业的平均时长约是______h．
13．国家能源局印发《2023年能源工作指导意见》提出，结构转型深入推进．2023年，风电、光伏发电量占全社会用电量的比重不断增大，其中太阳能电池（光伏电池）产量达5.4亿千瓦．数据5.4亿用科学记数法表示为______．
14．分解因式：______．
15．如第15题图，点都在圆上，顺次连接，若，则______度．
第15题图
16．如第16题图，平行于轴的直线与函数和的图象分别相交于两点，分别连接，则的面积为______．
第16题图
17．如第17题图，在中，，按以下步骤作图：①以点为圆心，小于的长为半径．画弧，分别交于点；②分别以点为圆心，大于的长为半径画弧，两弧相交于点；③作射线，交边于点．若，则______．
第17题图
18．“圆材埋壁”是我国古代数学名著《九章算术》中的一个问题：“今有圆材，埋在壁中，不知大小．以锯锯之，深一寸，锯道长六寸．问：径几何？”意思是：如第18题图，为的直径，弦，垂足为寸，寸，则直径的长度为______寸．
第18题图
三、解答题（本大题8个小题，共66分.19、20题各6分；21、22题各8分；23、24题各9分；25、26题各10分．解答应写出必要的文字说明、证明过程或演算步骤）
19．（本题满分6分）
计算：
20．（本题满分6分）
先化简，再求值：，其中．
21．（本题满分8分）
如图，正方形中，点分别是边的中点，．分别连接交于点．
（1）求证：；
（2）求的度数．
22．（本题满分8分）
2022年4月21日新版《义务教育课程标准（2022年版）》颁布，某校结合“双减”政策和新课标要求，优化了课程设计，决定增设“足球”、“篮球”、“书法”、“木工”及“编程”等五门校本课程以进一步提升课后服务质量，促进学生全面健康发展，为优化师资配备，学校面向参与课后服务的部分学生开展了“你选修哪门课程”（要求必须选修一门且只能选修一门）的随机问卷调查，并根据调查数据绘制了如下两幅不完整的统计图：
请结合上述信息，解答下列问题：
（1）共有______名学生参与了本次问卷调查；“篮球”在扇形统计图中所对应的圆心角是______度；
（2）补全调查结果的条形统计图；
（3）小刚和小强分别从“足球”、“篮球”、“编程”三门校本课程中任选一门，请用列表法或画树状图法求出两人中至少有一人选到“编程”这门课程的概率．
23．（本题满分9分）
为深入贯彻党的二十大精神，全面落实习近平总书记关于“把红色资源利用好、把红色基因传承好”的重要指示精神，培养学生的爱国情怀和责任担当，某校计划组织高一的师生共1302人到韶山开展红色研学活动．已知1台A型大巴车可以坐乘客49人，每日租金960元，一台B型大巴车可以坐乘客37人，每日租金780元．
（1）若计划租赁A型大巴车比租赁B型大巴车多2辆，要让每一位师生都有座位，且每辆汽车恰好坐满，问需租赁A型大巴车和B型大巴车各多少辆？
（2）为确保研学活动安全与效果，学校决定再增派两位校级领导带队，若计划租赁两种型号的大巴车共32台，且总费用不超过27200元，共有哪几种租赁方案？请指出费用最低的一种方案，并求出相应的费用．
24．（本题满分9分）
如图①是放置在水平桌面上的台灯的截面示意图，台灯底座的高为，长度均为的连杆与始终在同一平面上．
（1）转动连杆，使成平角，，如图②，求连杆端点离桌面的高度是多少？
（2）将图②中的连杆绕点顺时针旋转，使，再将连杆绕点逆时针旋转，使，如图③，此时连杆端点离桌面的高度又是多少？（结果精确到，参考数据：）
25．（本题满分10分）
如图①，在平面直角坐标系中，抛物线与轴交于两点（点在点的左侧），与轴交于点，连接．
（1）请你直接写出两点的坐标，并求直线的表达式．
（2）如图②，点为直线上方抛物线上一动点，设点的横坐标为，以点为圆心的圆与直线相切，当的半径最大时，求的值．
（3）设点是抛物线对称轴上任意一点，点是抛物线上任意一点．是否存在这样的点，使以为顶点的四边形是平行四边形？若存在，请直接写出点的坐标，若不存在，请说明理由．
26．（本题满分10分）
【问题探究】
综合实践课上，老师给出这样一个问题要求同学们进行小组合作探究：
如图①，在中，，点在边上，．探究图中线段之间的数量关系．
小红同学这一个学习小组探究此问题的方法是：
将绕点逆时针暶转，得到，连接（如图②），由图形旋转的性质和等腰直角三角形的性质以及，可证，得．即可得出之间的数量关系．
（1）请你根据小红同学这一学习小组的探究方法，写出探究结论：
在图②中，______度，之间的数量关系是______．
【问题延伸】
（2）小明同学这一学习小组在上述探究的基础上，又进行了如下问题的探究：
如图③，在正方形中，点分别是边上的动点，连接交于，若．请你帮小明同学这一学习小组完成如下猜想：
ⅰ）线段的数量关系是______；
ⅱ）线段的数量关系是______；
请任选一个你的猜想说明理由．
【问题解决】
（3）请根据上述探究方法，解决如下问题：如图④，已知点，点，点位于轴正半轴，，试求出点的坐标．
湘潭市2024年新中考模拟试题答案（定稿）
一、选择题（本大题共10个小题，每小题3分，满分30分．）
1．D 2．D 3．C 4．C 5．B 6．D 7．A 8．C 9．C 10．A
二、填空题（本题共8个小题，每小题3分，共24分．）
11．2024 12．1.5 13． 14． 15．60 16．2 17．10 18．10
三．解答题（本大题8个小题，共66分.19、20题各6分；21、22题各8分；23、24题各9分；25、26题各10分．按步骤分步计分参考标准如下）
19．解：原式
20．解：原式
当时，原式
21．证明：（1）四边形是正方形
又点分别是边的中点
又，
（2），，
，，
即，
22．（1）60，120
（2）补全条形统计图如下：
（3）把“足球”、“篮球”、“编程”三门校本课程记为A、B、C，画树状图如下：
共有9种等可能的结果，其中小刚和小强两人至少有一人选到编程的结果共有5种，
两人至少有一人选到编程
23．解：（1）设租赁A型大巴车x辆，B型大巴车y辆，由题意得：
解得
答：租赁型大巴车16辆，型大巴车14辆．
（2）设租赁型大巴车辆，租赁型大巴车（32-a）辆，则由题意得：
解得：
为正整数
．．
有三种方案，第一种：A型大巴车10辆，B型大巴车22辆，
总费用为最低
第二种：A型大巴车11辆，B型大巴车21辆，
总费用为
第三种：A型大巴车12辆，B型大巴车20辆，
总费用为
或：设总费用为元，则有：
当取最小值10时．总费用有最小值，最小值为26760元
24．（1）解：过点作，垂足，
在中，，
，．
答：D离桌面的高度为．
（2）过点作，垂足为，
过点作，垂足，过作垂足为交于点．
由题意可得
在中，
在中，
答：此时离桌面的高度约为．
25．解：（1）点，点
设的解析式为，把分别代入得：
解得：
直线表达式为
（2）过作轴的垂线交直线于点
设
点为直线上方
过作直线的垂线交直线于点
则，
是的切线即的半径
当时，取最大值，此时取最大值为，
法二：设直线交轴于，当直线与抛物线相切时，半径最大
设，则只有一个解
，即
即
（3）点或或
26．（1）
（2）① ②
选择猜想②证明过程如下：
将绕点按逆时针方向旋转，使与重合，得到：
，
．即点在同一条直线上．
，，
，，
在和中，，
，，
，．
（3）解法一：如图，在轴上截取，连接，可得
由（2）中的结论有
即：
，，
解法二：如图，在轴正半轴上截取，连接，可得
，
时长
2.5
2
1.5
1
0.5
人数
1
2
4
2
1