题型二 规律探索 类型二 图形规律（专题训练）-中考数学二轮复习满分冲刺题型突破（全国通用）

这是一份题型二 规律探索 类型二 图形规律（专题训练）-中考数学二轮复习满分冲刺题型突破（全国通用），文件包含题型二规律探索类型二图形规律专题训练原卷版docx、题型二规律探索类型二图形规律专题训练解析版docx等2份试卷配套教学资源，其中试卷共38页， 欢迎下载使用。

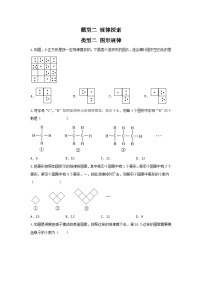
A．39B．44C．49D．54
【答案】B
【分析】根据各图形中木棍的根数发现计算的规律，由此即可得到答案．
【详解】解：第①个图案用了根木棍，
第②个图案用了根木棍，
第③个图案用了根木棍，
第④个图案用了根木棍，
……，
第⑧个图案用的木棍根数是根，
故选：B．
【点睛】此题考查了图形类规律的探究，正确理解图形中木棍根数的变化规律由此得到计算的规律是解题的关键．
2．（2023·重庆·统考中考真题）用圆圈按如图所示的规律拼图案，其中第①个图案中有2个圆圈，第②个图案中有5个圆圈，第③个图案中有8个圆圈，第④个图案中有11个圆圈，…，按此规律排列下去，则第⑦个图案中圆圈的个数为（ ）

A．14B．20C．23D．26
【答案】B
【分析】根据前四个图案圆圈的个数找到规律，即可求解.
【详解】解：因为第①个图案中有2个圆圈，；
第②个图案中有5个圆圈，；
第③个图案中有8个圆圈，；
第④个图案中有11个圆圈，；
…，
所以第⑦个图案中圆圈的个数为；
故选：B.
【点睛】本题考查了图形类规律探究，根据前四个图案圆圈的个数找到第n个图案的规律为是解题的关键.
3.如图，小正方形是按一定规律摆放的，下面四个选项中的图片，适合填补图中空白处的是
A．B．C．D．
【答案】D
【解析】由题意知，原图形中各行、各列中点数之和为10，符合此要求的只有，故选D．
【名师点睛】本题主要考查图形的变化规律，解题的关键是得出原图形中各行、各列中点数之和为10．
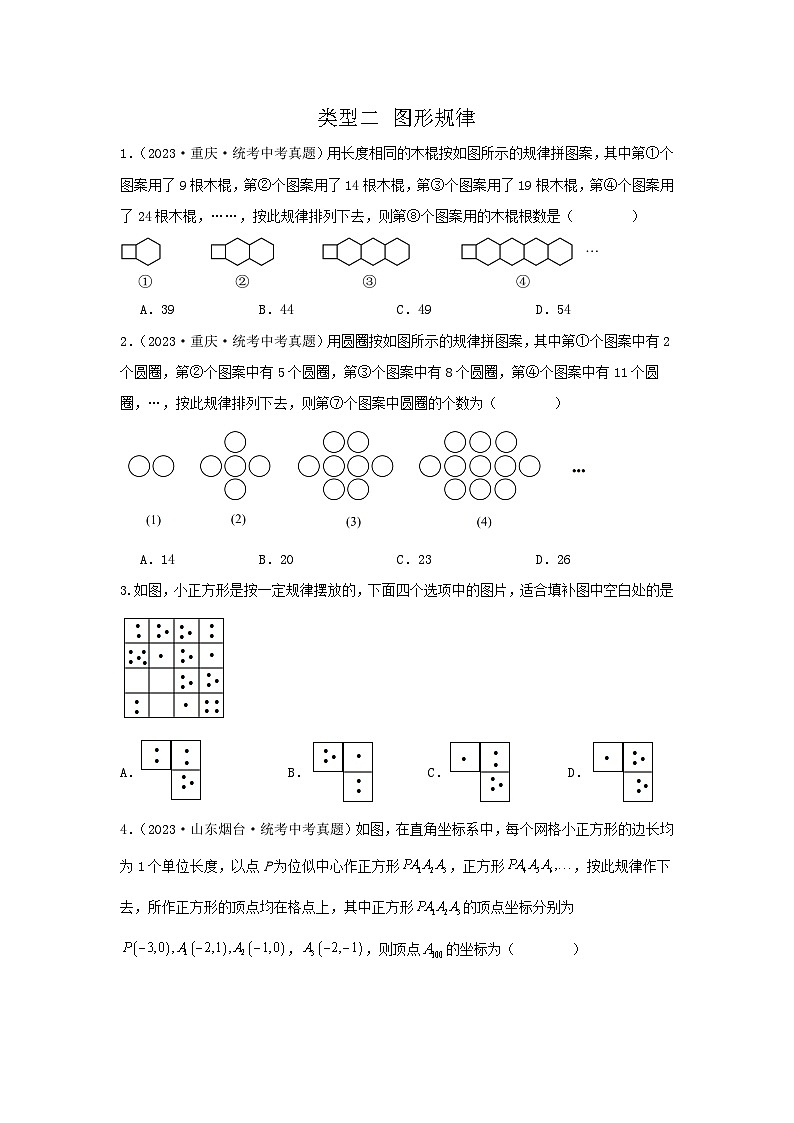
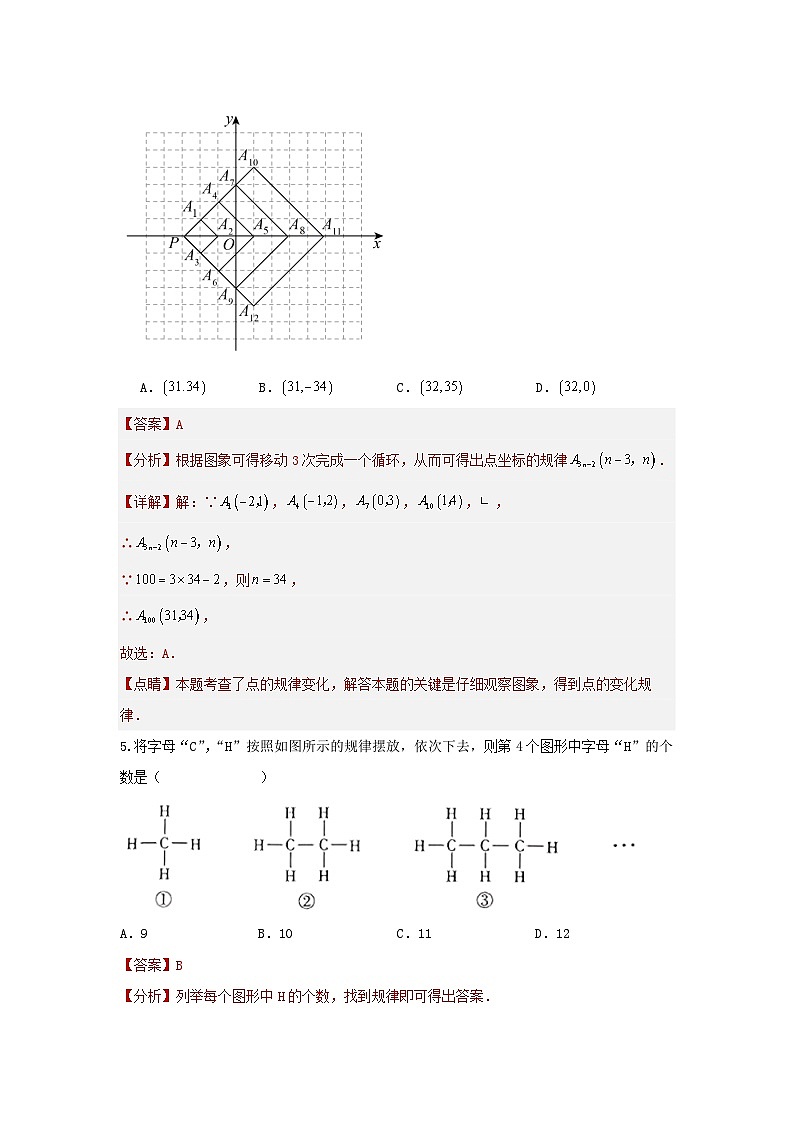
4．（2023·山东烟台·统考中考真题）如图，在直角坐标系中，每个网格小正方形的边长均为1个单位长度，以点P为位似中心作正方形，正方形，按此规律作下去，所作正方形的顶点均在格点上，其中正方形的顶点坐标分别为，，则顶点的坐标为（ ）

A．B．C．D．
【答案】A
【分析】根据图象可得移动3次完成一个循环，从而可得出点坐标的规律．
【详解】解：∵，，，，，
∴，
∵，则，
∴，
故选：A．
【点睛】本题考查了点的规律变化，解答本题的关键是仔细观察图象，得到点的变化规律．
5.将字母“C”，“H”按照如图所示的规律摆放，依次下去，则第4个图形中字母“H”的个数是（ ）
A．9B．10C．11D．12
【答案】B
【分析】列举每个图形中H的个数，找到规律即可得出答案．
【详解】解：第1个图中H的个数为4，
第2个图中H的个数为4+2，
第3个图中H的个数为4+2×2，
第4个图中H的个数为4+2×3=10，故选：B．
【点睛】本题考查了规律型：图形的变化类，通过列举每个图形中H的个数，找到规律：每个图形比上一个图形多2个H是解题的关键．
6．（2023·四川达州·统考中考真题）如图，四边形是边长为的正方形，曲线是由多段的圆心角的圆心为，半径为；的圆心为，半径为的圆心依次为循环，则的长是（ ）

A．B．C．D．
【答案】A
【分析】曲线是由一段段90度的弧组成的，半径每次比前一段弧半径，得到，，得出半径，再计算弧长即可．
【详解】解：由图可知，曲线是由一段段90度的弧组成的，半径每次比前一段弧半径，
，，，，
，，，，
，
，，
故的半径为，
的弧长．
故选A
【点睛】此题主要考查了弧长的计算，弧长的计算公式：，找到每段弧的半径变化规律是解题关键．
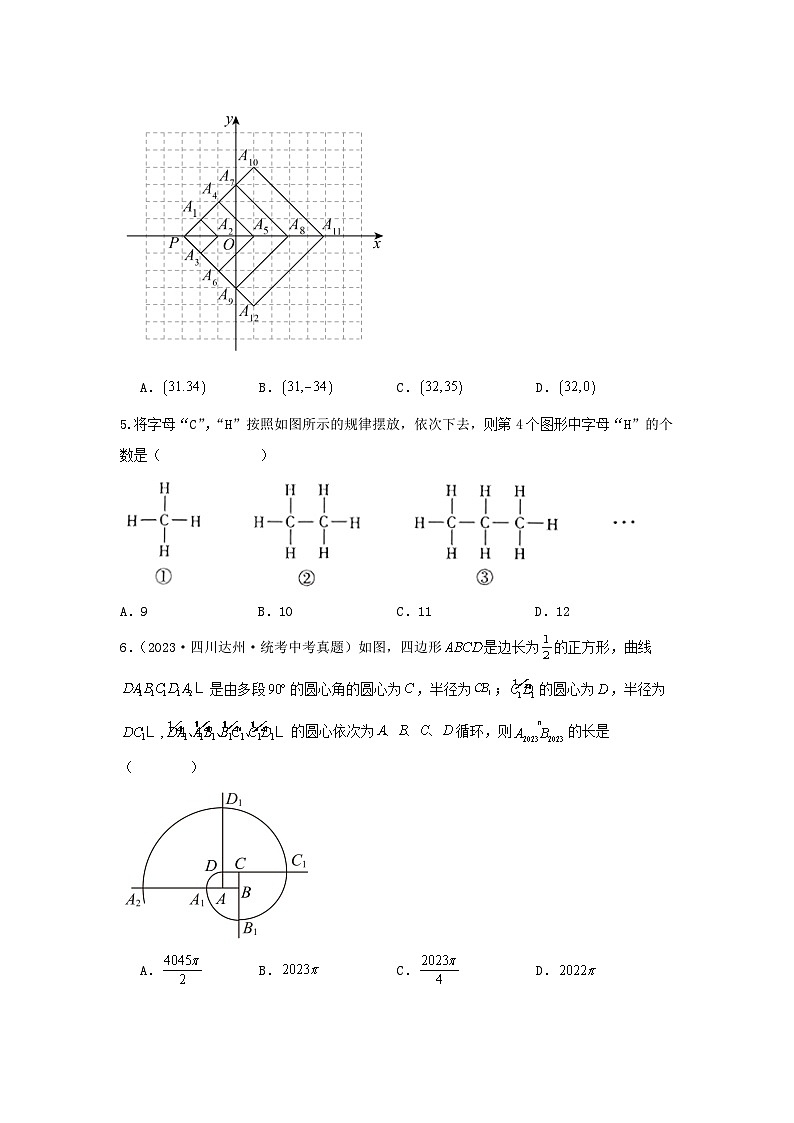
7.把菱形按照如图所示的规律拼图案，其中第①个图案中有1个菱形，第②个图案中有3个菱形，第③个图案中有5个菱形，…，按此规律排列下去，则第⑥个图案中菱形的个数为（ ）
A．15B．13C．11D．9
【答案】C
【分析】根据第①个图案中菱形的个数：；第②个图案中菱形的个数：；第③个图案中菱形的个数：；…第n个图案中菱形的个数：，算出第⑥个图案中菱形个数即可．
【详解】解：∵第①个图案中菱形的个数：；
第②个图案中菱形的个数：；
第③个图案中菱形的个数：；…
第n个图案中菱形的个数：，
∴则第⑥个图案中菱形的个数为：，故C正确．故选：C．
【点睛】本题主要考查的是图案的变化，解题的关键是根据已知图案归纳出图案个数的变化规律．
8.如图是用黑色棋子摆成的美丽图案，按照这样的规律摆下去，第10个这样的图案需要黑色棋子的个数为（ ）
A．148B．152C．174D．202
【分析】观察各图可知，后一个图案比前一个图案多2（n+3）枚棋子，然后写成第n个图案的通式，再取n＝10进行计算即可求解．
【解析】根据图形，第1个图案有12枚棋子，
第2个图案有22枚棋子，
第3个图案有34枚棋子，
…
第n个图案有2（1+2+…+n+2）+2（n﹣1）＝n2+7n+4枚棋子，
故第10个这样的图案需要黑色棋子的个数为102+7×10+4＝100+70+4＝174（枚）．
故选：C．
9.把黑色三角形按如图所示的规律拼图案，其中第①个图案中有1个黑色三角形，第②个图案中有3个黑色三角形，第③个图案中有6个黑色三角形，…，按此规律排列下去，则第⑤个图案中黑色三角形的个数为（ ）
A．10B．15C．18D．21
【分析】根据前三个图案中黑色三角形的个数得出第n个图案中黑色三角形的个数为1+2+3+4+……+n，据此可得第⑤个图案中黑色三角形的个数．
【解析】∵第①个图案中黑色三角形的个数为1，
第②个图案中黑色三角形的个数3＝1+2，
第③个图案中黑色三角形的个数6＝1+2+3，
……
∴第⑤个图案中黑色三角形的个数为1+2+3+4+5＝15，
故选：B．
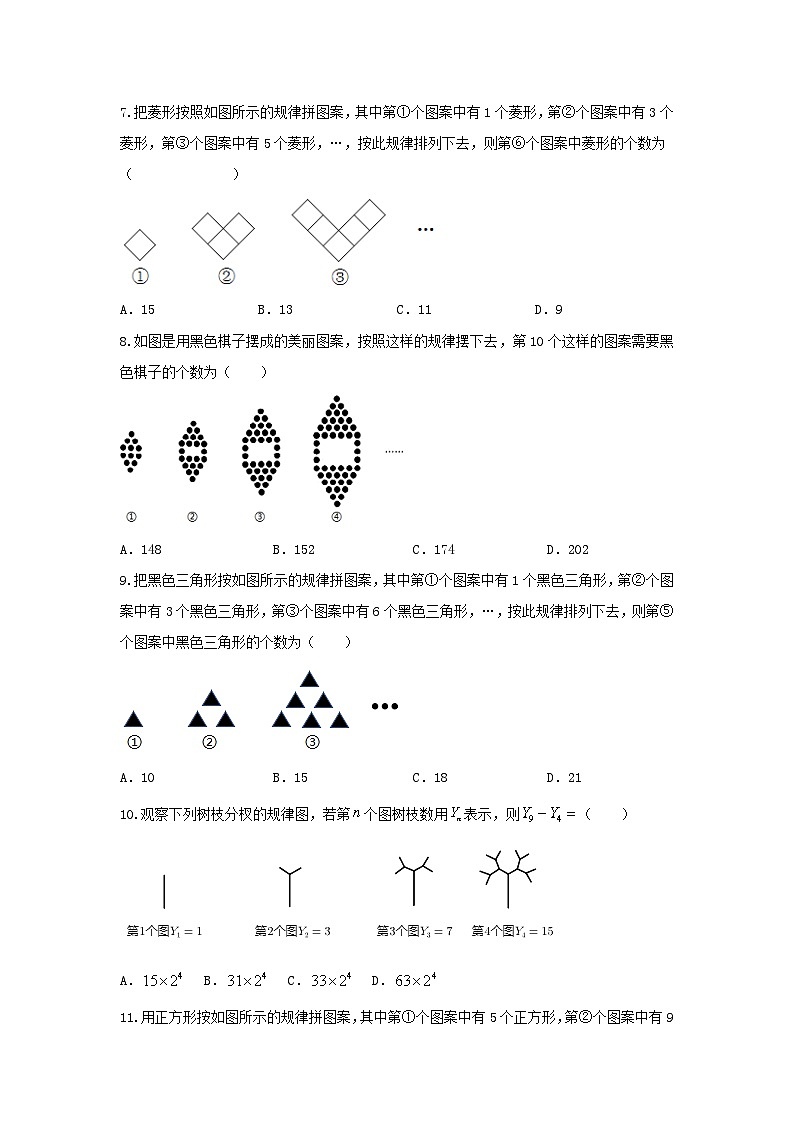
10.观察下列树枝分杈的规律图，若第个图树枝数用表示，则（ ）
A．B．C．D．
【答案】B
【分析】
根据题目中的图形，可以写出前几幅图中树枝分杈的数量，从而可以发现树枝分杈的变化规律，进而得到规律，代入规律求解即可．
【详解】
解：由图可得到：

则：，
∴，
故答案选：B．
【点睛】
本题考查图形规律，解答本题的关键是明确题意，利用数形结合的思想解答．
11.用正方形按如图所示的规律拼图案，其中第①个图案中有5个正方形，第②个图案中有9个正方形，第③个图案中有13个正方形，第④个图案中有17个正方形，此规律排列下去，则第⑨个图案中正方形的个数为（ ）
A．32B．34C．37D．41
【答案】C
【分析】第1个图中有5个正方形，第2个图中有9个正方形，第3个图中有13个正方形，……，由此可得：每增加1个图形，就会增加4个正方形，由此找到规律，列出第n个图形的算式，然后再解答即可．
【详解】解：第1个图中有5个正方形；
第2个图中有9个正方形，可以写成：5+4=5+4×1；
第3个图中有13个正方形，可以写成：5+4+4=5+4×2；
第4个图中有17个正方形，可以写成：5+4+4+4=5+4×3；．．．
第n个图中有正方形，可以写成：5+4（n-1）=4n+1；
当n=9时，代入4n+1得：4×9+1=37．故选：C．
【点睛】本题主要考查了图形的变化规律以及数字规律，通过归纳与总结结合图形得出数字之间的规律是解决问题的关键．
12.在平面直角坐标系中，等边如图放置，点的坐标为，每一次将绕着点逆时针方向旋转，同时每边扩大为原来的2倍，第一次旋转后得到，第二次旋转后得到，…，依次类推，则点的坐标为（ ）
A．B．
C．D．
【答案】C
【分析】
由题意，点A每6次绕原点循环一周，利用每边扩大为原来的2倍即可解决问题．
【详解】
解：由题意，点A每6次绕原点循环一周，
，
点在第四象限，， ，
点的横坐标为，纵坐标为，
，
故选：C．
【点睛】
本题考查坐标与图形变化旋转，规律型问题，解题的关键是理解题意，学会探究规律的方法，属于中考常考题型．
13.如图，用大小相同的小正方形拼大正方形，拼第1个正方形需要4个小正方形，拼第2个正方形需要9个小正方形…，按这样的方法拼成的第（n+1）个正方形比第n个正方形多 个小正方形．
【分析】观察不难发现，所需要的小正方形的个数都是平方数，然后根据相应的序数与正方形的个数的关系找出规律解答即可．
【解析】∵第1个正方形需要4个小正方形，4＝22，
第2个正方形需要9个小正方形，9＝32，
第3个正方形需要16个小正方形，16＝42，
…，
∴第n+1个正方形有（n+1+1）2个小正方形，
第n个正方形有（n+1）2个小正方形，
故拼成的第n+1个正方形比第n个正方形多（n+2）2﹣（n+1）2＝2n+3个小正方形．
故答案为：2n+3．
14．（2023·四川遂宁·统考中考真题）烷烃是一类由碳、氢元素组成的有机化合物，在生产生活中可作为燃料、润滑剂等原料，也可用于动、植物的养护．通常用碳原子的个数命名为甲烷、乙烷、丙烷、……、癸烷（当碳原子数目超过个时即用汉文数字表示，如十一烷、十二烷……）等，甲烷的化学式为，乙烷的化学式为，丙烷的化学式为……，其分子结构模型如图所示，按照此规律，十二烷的化学式为 ．
【答案】
【分析】根据碳原子的个数，氢原子的个数，找到规律，即可求解．
【详解】解：甲烷的化学式为，
乙烷的化学式为，
丙烷的化学式为……，
碳原子的个数为序数，氢原子的个数为碳原子个数的2倍多2个，
十二烷的化学式为，
故答案为：．
【点睛】本题考查了规律题，找到规律是解题的关键．
15．（2023·湖北十堰·统考中考真题）用火柴棍拼成如下图案，其中第①个图案由4个小等边三角形围成1个小菱形，第②个图案由6个小等边三角形围成2个小菱形，……，若按此规律拼下去，则第n个图案需要火柴棍的根数为 （用含n的式子表示）．

【答案】/
【分析】当时，有个三角形；当时，有个三角形；当时，有个三角形；第n个图案有个三角形，每个三角形用三根计算即可．
【详解】解：当时，有个三角形；
当时，有个三角形；
当时，有个三角形；
第n个图案有个三角形，
每个三角形用三根，
故第n个图案需要火柴棍的根数为．
故答案为：．
【点睛】本题考查了整式的加减的数字规律问题，熟练掌握规律的探索方法是解题的关键．
16．（2023·山西·统考中考真题）如图是一组有规律的图案，它由若干个大小相同的圆片组成．第1个图案中有4个白色圆片，第2个图案中有6个白色圆片，第3个图案中有8个白色圆片，第4个图案中有10个白色圆片，…依此规律，第n个图案中有 个白色圆片（用含n的代数式表示）

【答案】
【分析】由于第1个图案中有4个白色圆片，第2个图案中有6个白色圆片，第3个图案中有8个白色圆片，第4个图案中有10个白色圆片，，可得第个图案中有白色圆片的总数为．
【详解】解：第1个图案中有4个白色圆片，
第2个图案中有6个白色圆片，
第3个图案中有8个白色圆片，
第4个图案中有10个白色圆片，
，
∴第个图案中有个白色圆片．
故答案为：．
【点睛】此题考查图形的变化规律，通过从一些特殊的数字变化中发现不变的因素或按规律变化的因素，然后推广到一般情况．解题关键是总结归纳出图形的变化规律．
17．（2023·黑龙江绥化·统考中考真题）在求的值时，发现：，，从而得到．按此方法可解决下面问题．图（1）有1个三角形，记作；分别连接这个三角形三边中点得到图（2），有5个三角形，记作；再分别连接图（2）中间的小三角形三边中点得到图（3），有9个三角形，记作；按此方法继续下去，则 ．（结果用含n的代数式表示）

【答案】/
【分析】根据题意得出，进而即可求解．
【详解】解：依题意，，
∴，
故答案为：．
【点睛】本题考查了图形类规律，找到规律是解题的关键．
18.观察下列图中所示的一系列图形，它们是按一定规律排列的，依照此规律，第2019个图形中共有__________个〇．
【答案】6058
【解析】由图可得，第1个图象中〇的个数为：1+3×1=4，
第2个图象中〇的个数为：1+3×2=7，
第3个图象中〇的个数为：1+3×3=10，
第4个图象中〇的个数为：1+3×4=13，
…
∴第2019个图形中共有：1+3×2019=1+6057=6058个〇，故答案为：6058．
【名师点睛】本题考查图形的变化类，解答本题的关键是明确题意，发现图形中〇的变化规律，利用数形结合的思想解答．
19．（2023·山东泰安·统考中考真题）已知，都是边长为2的等边三角形，按下图所示摆放．点都在x轴正半轴上，且，则点的坐标是 ．

【答案】
【分析】先确定前几个点的坐标，然后归纳规律，按规律解答即可．
【详解】解：由图形可得：
如图：过作轴，

∵
∴
∴,
同理：
∴为偶数，为奇数；
∵，2023为奇数
∴．
故答案为．
【点睛】本题主要考查了等边三角形的性质、解直角三角形、坐标规律等知识点，先求出几个点、发现规律是解答本题的关键．
20.如图，每一图中有若干个大小不同的菱形，第1幅图中有1个菱形，第2幅图中有3个菱形，第3幅图中有5个菱形，如果第n幅图中有2019个菱形，则n=__________．
【答案】1010
【解析】根据题意分析可得：第1幅图中有1个．第2幅图中有2×2-1=3个．第3幅图中有2×3-1=5个．第4幅图中有2×4-1=7个．…
可以发现，每个图形都比前一个图形多2个．故第n幅图中共有（2n-1）个．
当图中有2019个菱形时，2n-1=2019，n=1010，故答案为：1010．
【名师点睛】本题考查规律型中的图形变化问题，难度适中，要求学生通过观察，分析、归纳并发现其中的规律．
21.观察下列图形规律，当图形中的“○”的个数和“．”个数差为2022时，n的值为____________．
【答案】不存在
【分析】首先根据n=1、2、3、4时，“•”的个数分别是3、6、9、12，判断出第n个图形中“•”的个数是3n；然后根据n=1、2、3、4，“○”的个数分别是1、3、6、10，判断出第n个“○”的个数是；最后根据图形中的“○”的个数和“．”个数差为2022，列出方程，解方程即可求出n的值是多少即可．
【详解】解：∵n=1时，“•”的个数是3=3×1；
n=2时，“•”的个数是6=3×2；
n=3时，“•”的个数是9=3×3；
n=4时，“•”的个数是12=3×4；
……
∴第n个图形中“•”的个数是3n；
又∵n=1时，“○”的个数是1=；
n=2时，“○”的个数是，
n=3时，“○”的个数是，
n=4时，“○”的个数是，
……
∴第n个“○”的个数是，
由图形中的“○”的个数和“．”个数差为2022
①，②
解①得：无解
解②得：
故答案为：不存在
【点睛】本题考查了图形类规律，解一元二次方程，找到规律是解题的关键．
22．（2023·四川广安·统考中考真题）在平面直角坐标系中，点在轴的正半轴上，点在直线上，若点的坐标为，且均为等边三角形．则点的纵坐标为 ．

【答案】
【分析】过点作轴，交直线于点，过点作轴于点，先求出，再根据等边三角形的性质、等腰三角形的判定可得，然后解直角三角形可得的长，即可得点的纵坐标，同样的方法分别求出点的纵坐标，最后归纳类推出一般规律，由此即可得．
【详解】解：如图，过点作轴，交直线于点，过点作轴于点，

，
，
当时，，即，
，
，
是等边三角形，
，
，
，
，即点的纵坐标为，
同理可得：点的纵坐标为，
点的纵坐标为，
点的纵坐标为，
归纳类推得：点的纵坐标为（为正整数），
则点的纵坐标为，
故答案为：．
【点睛】本题考查了点坐标的规律探索、等边三角形的性质、正比例函数的应用、解直角三角形等知识点，正确归纳类推出一般规律是解题关键．
23.将黑色圆点按如图所示的规律进行排列，图中黑色圆点的个数依次为：1，3，6，10，……，将其中所有能被3整除的数按从小到大的顺序重新排列成一组新数据，则新数据中的第33个数为___________．
【答案】1275
【分析】
首先得到前n个图形中每个图形中的黑色圆点的个数，得到第n个图形中的黑色圆点的个数为，再判断其中能被3整除的数，得到每3个数中，都有2个能被3整除，再计算出第33个能被3整除的数所在组，为原数列中第50个数，代入计算即可．
【详解】
解：第①个图形中的黑色圆点的个数为：1，
第②个图形中的黑色圆点的个数为：=3，
第③个图形中的黑色圆点的个数为：=6，
第④个图形中的黑色圆点的个数为：=10，
第n个图形中的黑色圆点的个数为，
则这列数为1，3，6，10，15，21，28，36，45，55，66，78，91，，
其中每3个数中，都有2个能被3整除，
33÷2=161，
16×3+2=50，
则第33个被3整除的数为原数列中第50个数，即=1275，
故答案为：1275．
【点睛】
此题考查了规律型：图形的变化类，关键是通过归纳与总结，得到其中的规律．
24.如图，3条直线两两相交最多有3个交点，4条直线两两相交最多有6个交点，按照这样的规律，则20条直线两两相交最多有______个交点
【答案】190
【分析】
根据题目中的交点个数，找出条直线相交最多有的交点个数公式：．
【详解】
解：2条直线相交有1个交点；
3条直线相交最多有个交点；
4条直线相交最多有个交点；
5条直线相交最多有个交点；
20条直线相交最多有．
故答案为：190．
【点睛】
本题考查的是多条直线相交的交点问题，解答此题的关键是找出规律，即条直线相交最多有．
25.如图，用火柴棍拼成一个由三角形组成的图形，拼第一个图形共需要3根火柴棍，拼第二个图形共需要5根火柴棍；拼第三个图形共需要7根火柴棍；……照这样拼图，则第n个图形需要___________根火柴棍．
【答案】2n+1
【分析】
分别得到第一个、第二个、第三个图形需要的火柴棍，找到规律，再总结即可．
【详解】
解：由图可知：
拼成第一个图形共需要3根火柴棍，
拼成第二个图形共需要3+2=5根火柴棍，
拼成第三个图形共需要3+2×2=7根火柴棍，
拼成第n个图形共需要3+2×（n-1）=2n+1根火柴棍，
故答案为：2n+1．
【点睛】
此题考查图形的变化规律，找出图形之间的联系，得出运算规律解决问题．
26.如图都是由同样大小的小球按一定规律排列的，依照此规律排列下去，第___个图形共有210个小球．
【答案】20
【分析】
根据已知图形得出第n个图形中黑色三角形的个数为1+2+3++n=，列一元二次方程求解可得．
【详解】
解：∵第1个图形中黑色三角形的个数1，
第2个图形中黑色三角形的个数3=1+2，
第3个图形中黑色三角形的个数6=1+2+3，
第4个图形中黑色三角形的个数10=1+2+3+4，
……
∴第n个图形中黑色三角形的个数为1+2+3+4+5++n=，
当共有210个小球时，
，
解得：或(不合题意，舍去)，
∴第个图形共有210个小球．
故答案为：．
【点睛】
本题考查了图形的变化规律，解一元二次方程，解题的关键是得出第n个图形中黑色三角形的个数为1+2+3+……+n．
27.如图，由两个长为2，宽为1的长方形组成“7”字图形
（1）将一个“7”字图形按如图摆放在平面直角坐标系中，记为“7”字图形ABCDEF，其中顶点A位于x轴上，顶点B，D位于y轴上，O为坐标原点，则的值为__________．
（2）在（1）的基础上，继续摆放第二个“7”字图形得顶点F1，摆放第三个“7”字图形得顶点F2，依此类推，…，摆放第n个“7”字图形得顶点Fn-1，…，则顶点F2019的坐标为__________．
【答案】（1）；（2）
【解析】（1）∵∠ABO+∠DBC=90°，∠ABO+∠OAB=90°，∴∠DBC=∠OAB，
∵∠AOB=∠BCD=90°，∴△AOB∽△BCD，∴，
∵DC=1，BC=2，∴=，故答案为：．
（2过C作CM⊥y轴于M，过M1作M1N⊥x轴，过F作FN1⊥x轴．
根据勾股定理易证得BD，CM=OA=，DM=OB=AN=，∴C（，），
∵AF=3，M1F=BC=2，∴AM1=AF-M1F=3-2=1，∴△BOA≌ANM1（AAS），∴NM1=OA=，
∵NM1∥FN1，∴，
∴FN1=，∴AN1=，∴ON1=OA+AN1=，∴F（，），
同理，
F1（），即（），
F2（），即（），
F3（），即（），
F4（），即（ ），
…
F2019（），即（， ），
故答案为：（，）．
【名师点睛】此题考查了平面图形的有规律变化，要求学生通过观察图形，分析、归纳并发现其中的规律，并应用规律解决问题是解题的关键
28.如图，正方形中，，AB与直线l所夹锐角为，延长交直线l于点，作正方形，延长交直线l于点，作正方形，延长交直线l于点，作正方形，…，依此规律，则线段________．
【答案】
【分析】
利用tan30°计算出30°角所对直角边，乘以2得到斜边，计算3次，找出其中的规律即可.
【详解】
∵AB与直线l所夹锐角为，正方形中，，
∴∠=30°，
∴=tan30°==1，
∴；
∵=1，∠=30°，
∴=tan30°=，
∴；
∴线段,
故答案为：.
【点睛】
本题考查了正方形的性质，特殊角三角函数值，含30°角的直角三角形的性质，规律思考，熟练进行计算，抓住指数的变化这个突破口求解是解题的关键.
29.如图，菱形中，，，延长至，使，以为一边，在的延长线上作菱形，连接，得到；再延长至，使，以为一边，在的延长线上作菱形，连接，得到……按此规律，得到，记的面积为，的面积为……的面积为，则_____．
【答案】
【分析】
由题意易得，则有为等边三角形，同理可得……. 都为等边三角形，进而根据等边三角形的面积公式可得，，……由此规律可得，然后问题可求解．
【详解】
解：∵四边形是菱形，
∴，，
∵，
∴，
∴，
∵，
∴，
∴为等边三角形，
同理可得……. 都为等边三角形，
过点B作BE⊥CD于点E，如图所示：
∴，
∴，
同理可得：，，……；
∴由此规律可得：，
∴；
故答案为．
【点睛】
本题主要考查菱形的性质、等边三角形的性质与判定及三角函数，熟练掌握菱形的性质、等边三角形的性质与判定及三角函数是解题的关键．
30.将一些相同的“〇”按如图所示的规律依次摆放，观察每个“龟图”的“〇”的个数，则第30个“龟图”中有___________个“〇”．
【答案】875
【分析】
设第n个“龟图”中有an个“〇”（n为正整数），观察“龟图”，根据给定图形中“〇”个数的变化可找出变化规律“an＝n2−n＋5（n为正整数）”，再代入n＝30即可得出结论．
【详解】
解：设第n个“龟图”中有an个“〇”（n为正整数）．
观察图形，可知：a1＝1＋2＋2＝5，a2＝1＋3＋12＋2＝7，a3＝1＋4＋22＋2＝11，a4＝1＋5＋32＋2＝17，…，
∴an＝1＋（n＋1）＋（n−1）2＋2＝n2−n＋5（n为正整数），
∴a30＝302−30＋5＝875．
故答案是：875．
【点睛】
本题考查了规律型：图形的变化类，根据各图形中“〇”个数的变化找出变化规律“an＝n2−n＋5（n为正整数）”是解题的关键．
31.下面各图形是由大小相同的三角形摆放而成的，图①中有1个三角形，图②中有5个三角形，图③中有11个三角形，图④中有19个三角形…，依此规律，则第个图形中三角形个数是_______．
【答案】
【分析】
此题只需分成上下两部分即可找到其中规律，上方的规律为(n-1)，下方规律为n2，结合两部分即可得出答案．
【详解】
解：将题意中图形分为上下两部分，
则上半部规律为：0、1、2、3、4……n-1，
下半部规律为：12、22、32、42……n2，
∴上下两部分统一规律为：．
故答案为：．
【点睛】
本题主要考查的图形的变化规律，解题的关键是将图形分为上下两部分分别研究
32.如图是一组有规律的图案，它们是由边长相等的正三角形组合而成，第1个图案有4个三角形，第2个图案有7个三角形，第3个图案有10个三角形…按此规律摆下去，第n个图案有 个三角形（用含n的代数式表示）．
【分析】根据图形的变化发现规律，即可用含n的代数式表示．
【解析】第1个图案有4个三角形，即4＝3×1+1
第2个图案有7个三角形，即7＝3×2+1
第3个图案有10个三角形，即10＝3×3+1
…
按此规律摆下去，
第n个图案有（3n+1）个三角形．
故答案为：（3n+1）．
33.如图，四边形ABCD是矩形，延长DA到点E，使AE＝DA，连接EB，点F1是CD的中点，连接EF1，BF1，得到△EF1B；点F2是CF1的中点，连接EF2，BF2，得到△EF2B；点F3是CF2的中点，连接EF3，BF3，得到△EF3B；…；按照此规律继续进行下去，若矩形ABCD的面积等于2，则△EFnB的面积为 ．（用含正整数n的式子表示）
【分析】先求得△EF1D的面积为1，再根据等高的三角形面积比等于底边的比可得EF1F2的面积，EF2F3的面积，…，EFn﹣1Fn的面积，以及△BCFn的面积，再根据面积的和差关系即可求解．
【解析】∵AE＝DA，点F1是CD的中点，矩形ABCD的面积等于2，
∴△EF1D和△EAB的面积都等于1，
∵点F2是CF1的中点，
∴△EF1F2的面积等于12，
同理可得△EFn﹣1Fn的面积为12n−1，
∵△BCFn的面积为2×12n÷2=12n，
∴△EFnB的面积为2+1﹣1−12−⋯−12n−1−12n=2﹣（1−12n）=2n+12n．
故答案为：2n+12n．