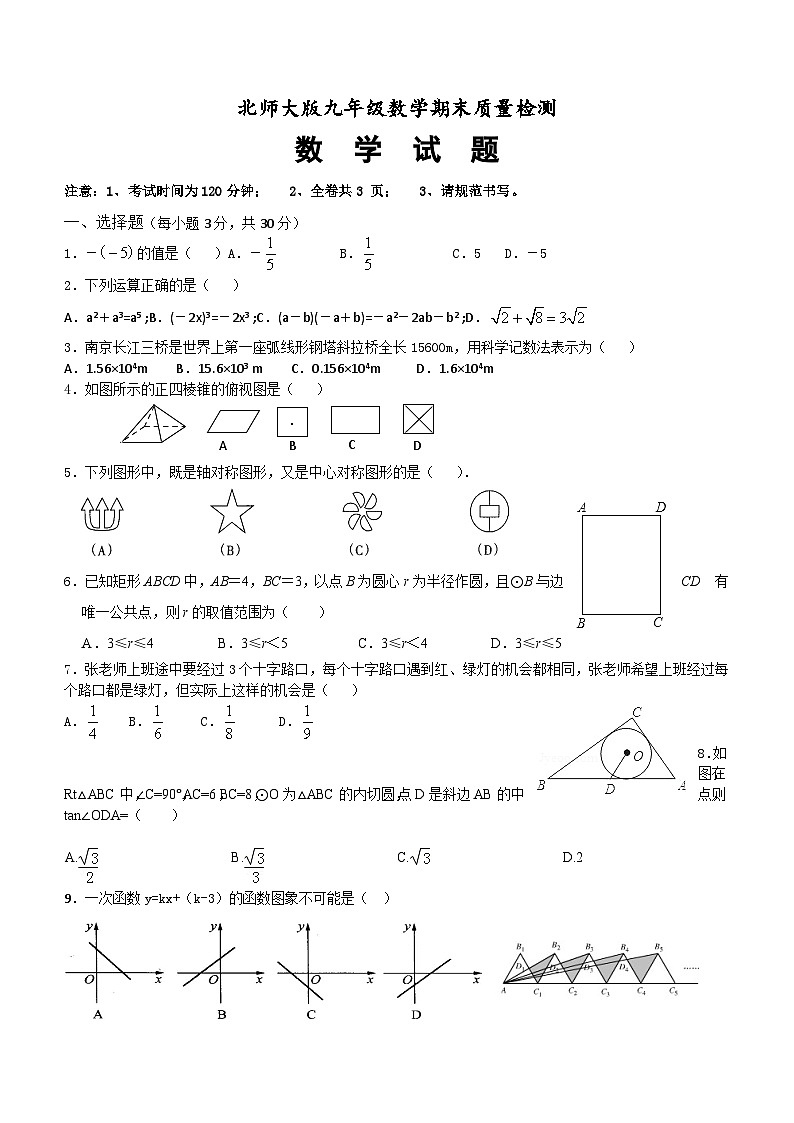
2023-2024学年北师大版数学九年级下册期末质量检测（含答案）

这是一份2023-2024学年北师大版数学九年级下册期末质量检测（含答案），共8页。试卷主要包含了考试时间为120分钟； 2等内容，欢迎下载使用。

注意：1、考试时间为120分钟； 2、全卷共3 页； 3、请规范书写。
一、选择题（每小题3分，共30分）
1．－的值是（ ）A．－ B． C．5 D．－5
2．下列运算正确的是（ ）
A．a2＋a3=a5 ;B．(－2x)3=－2x3 ;C．(a－b)(－a＋b)=－a2－2ab－b2 ;D．
3．南京长江三桥是世界上第一座弧线形钢塔斜拉桥全长15600m，用科学记数法表示为（ ）
A．1.56×104m B．15.6×103 m C．0.156×104m D．1.6×104m
4．如图所示的正四棱锥的俯视图是（ ）
·
A
B
C
D
5．下列图形中，既是轴对称图形，又是中心对称图形的是（ ）．

6．已知矩形ABCD中，AB＝4，BC＝3，以点B为圆心r为半径作圆，且⊙B与边CD有唯一公共点，则r的取值范围为（ ）
A．3≤r≤4B．3≤r＜5C．3≤r＜4D．3≤r≤5
7．张老师上班途中要经过3个十字路口，每个十字路口遇到红、绿灯的机会都相同，张老师希望上班经过每个路口都是绿灯，但实际上这样的机会是（ ）
A． B． C． D．
8．如图，在Rt△ABC中，∠C=90°，AC=6，BC=8，⊙O为△ABC的内切圆，点D是斜边AB的中点，则tan∠ODA=（ ）
9．一次函数y=kx+（k-3）的函数图象不可能是（ ）
10．如图，个边长为2的等边三角形有一条边在同一直线上，设△面积为，△面积为,…，△面积为，则等于（ ）
A． B． C． D．
二、填空题（每小题3分，共30分）
11.函数y＝＋中自变量x的取值范围是 .
12．不等式组的解集是 ．
13.在边长为3㎝、4㎝、5㎝的三角形白铁皮上剪下一个最大的圆，此圆的半径
为 ㎝.
某种品牌的手机经过四、五月份连续两次降价，每部售价由3200元降到了2500
元．设平均每月降价的百分率为，根据题意列出的方程是 ．
15.若关于的分式方程(x-a) /(x-1)-3/x=1 无解，则
16．如果正比例函数y = ax（）与反比例函数y =（）的图象有两个交点，其中一个交点的坐标为（－3，－2），那么另一个交点的坐标为 ．
17．如图所示，在等腰△ABC中，延长边AB到点D，延长边CA到点E，连接DE，恰有AD=BC=CE=DE．则∠BAC= ．
18．已知四边形ABCD中，∠B=90°，AD∥BC，AB=BC=8，CD=10，则这个四边形的面积是
19．已知：如图，在正方形ABCD外取一点E，连接AE、BE、DE．过点A作AE的垂线交DE于点P．若AE＝AP＝1，PB＝，则S正方形ABCD＝
20．如图，平面直角坐标系内，正三角形ABC的顶点B，C的坐标分别为（1，0），（3，0），过坐标原点O的一条直线分别与边AB，AC交于点M，N，若OM=MN，则点M的坐标为
三、解答题（共60分）
21.（满分5分）先化简，再求值:（）÷，
其中x＝,y＝.
22．（满分7分）已知△ABC在平面直角坐标系中的位置如图所示．
（1）分别写出图中点A和点C的坐标；
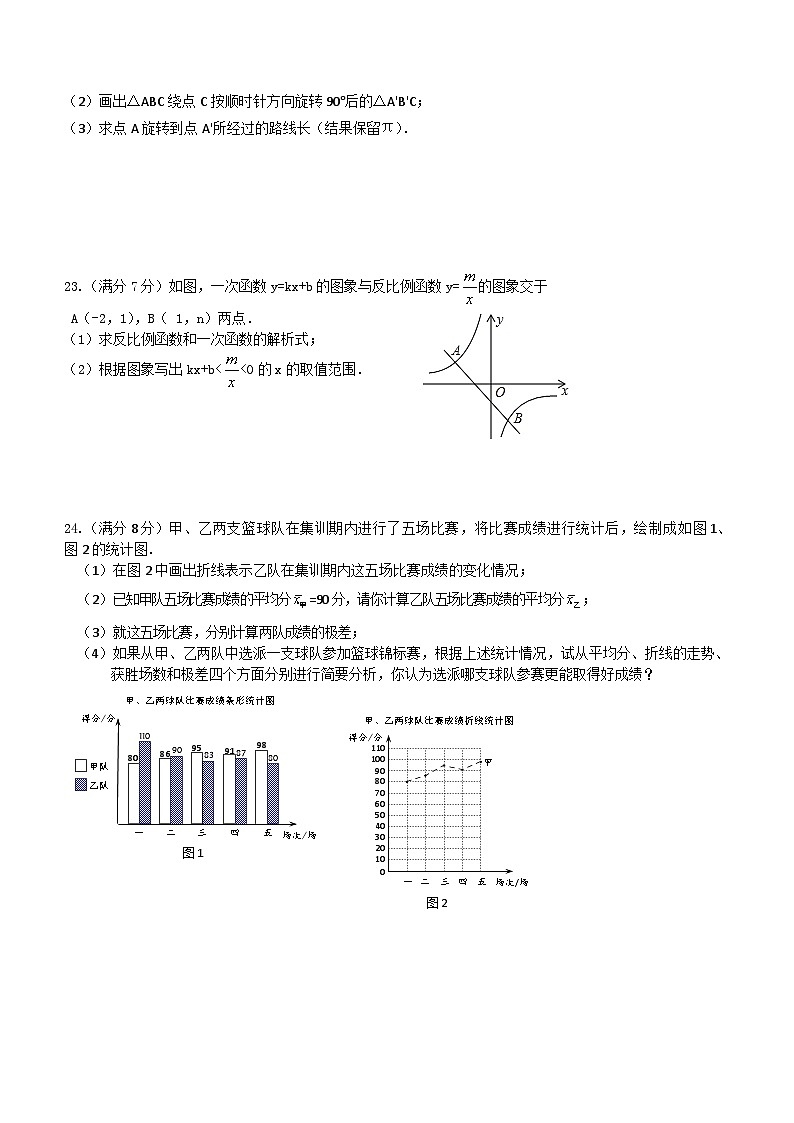
（2）画出△ABC绕点C按顺时针方向旋转90°后的△A'B'C；
（3）求点A旋转到点A'所经过的路线长（结果保留π）．
23.（满分7分）如图，一次函数y=kx+b的图象与反比例函数y=的图象交于
A（-2，1），B（1，n）两点．
（1）求反比例函数和一次函数的解析式；
（2）根据图象写出kx+b<<0的x的取值范围．
24.（满分8分）甲、乙两支篮球队在集训期内进行了五场比赛，将比赛成绩进行统计后，绘制成如图1、图2的统计图．
（1）在图2中画出折线表示乙队在集训期内这五场比赛成绩的变化情况；
（2）已知甲队五场比赛成绩的平均分=90分，请你计算乙队五场比赛成绩的平均分；
（3）就这五场比赛，分别计算两队成绩的极差；
甲、乙两球队比赛成绩折线统计图
图2
10
20
30
40
50
60
70
80
90
100
一
二
三
四
五
0
得分/分
甲
110
场次/场
/分
（4）如果从甲、乙两队中选派一支球队参加篮球锦标赛，根据上述统计情况，试从平均分、折线的走势、获胜场数和极差四个方面分别进行简要分析，你认为选派哪支球队参赛更能取得好成绩？
一
二
三
四
五
得分/分
80
110
86
90
91
87
95
83
98
80
甲、乙两球队比赛成绩条形统计图
甲队
乙队
图1
场次/场
D
C
B
A
②
①
25.（满分6分）在学习《测物体高度》时，为了测量雕塑（如图①）的高度，甲学生在二楼找到一点C，利用三角板测得雕塑顶端A点的仰角为，底部B点的俯角为，乙学生在五楼找到一点D，利用三角板测得A点的俯角为（如图②）.若已知CD为10米，请求出雕塑AB的高度．（结果精确到0.1米，参考数据）．
26.（满分8分）如图，AB切⊙O于点B，OA交⊙O于C点，过C作DC⊥OA交AB
于D，且BD：AD=1：2.
求∠A的正切值;
若OC =1，求AB及的长.
27．（满分9分）某大学毕业生响应国家“自主创业”的号召，投资开办了一个装饰品商店．该店采购进一种今年新上市的饰品进行了30天的试销售，购进价格为20元／件．销售结束后，得知日销售量P(件)与销售时间x(天)之间有如下关系：P=-2x+80(1≤x≤30，且x为整数)；又知前20天的销售价格 (元/件)与销售时间x(天)之间有如下关系： (1≤x≤20，且x为整数)，后10天的销售价格 (元/件)与销售时间x(天)之间有如下关系：=45(21≤x≤30，且x为整数)．
(1)试写出该商店前20天的日销售利润(元)和后l0天的日销售利润(元)分别与销售时间x(天)之间的函数关系式；
(2)请问在这30天的试销售中，哪一天的日销售利润最大?并求出这个最大利润．
注：销售利润＝销售收入一购进成本．
28．（满分10分）如图，抛物线交轴于A、B两点（A点在B点左侧），交轴于点C，已知B（8，0），，△ABC的面积为8.
P
C
O
E
F
A
B
（1）求抛物线的解析式；
（2）若动直线EF（EF∥轴）从点C开始，以每秒1个长度单位的速度沿轴负方向平移，且交轴、线段BC于E、F两点，动点P同时从点B出发，在线段OB上以每秒2个单位的速度向原点O运动。连结FP，设运动时间秒。当为何值时，的值最大，并求出最大值；
（3）在满足（2）的条件下，是否存在的值，使以P、B、F为顶点的三角形与△ABC相似。若存在，试求出的值；若不存在，请说明理由。
数 学 答 案
一、选择题：（共30分）
二、填空题：（共30分）
x<3； 12． ； 13． 1 ； 14．3200（或 或） 15． 1或－2 ； 16．（3，2） ；
17． 1000 ； 18. 40或88 ； 19．6＋； 20.（，）
三、解答题：（共60分）
21.（5分）
解：原式= EQ \F(2x,x2－y2) ÷ EQ \F(xy,x2－y2)= EQ \F(2x,x2－y2) × EQ \F(x2－y2,xy)= EQ \F(2,y)
当y＝时， EQ \F(2,y) ==
（7分）
解：⑴A(0,4)，C(3,1)； ⑵图略； ⑶ EQ \F(3\R(2),2)π．
23.（7分）（1）把A（-2，1）代入y=，得m=-2，
即反比例函数为y=-，则n=n=-2．
即B（1，-2），把A（-2，1），B（1，-2）代入y=kx+b，
求得k=-1，b=-1，所以y=-x-1．
（2）x>1
图2
10
20
30
40
50
60
70
80
90
100
一
二
三
四
五
0
得分/分
甲、乙两球队比赛成绩折线统计图
甲
110
场次/场
/分
乙
24.（8分）
解：（1）如图2；
（2）=90（分）；
（3）甲队成绩的极差是18分，乙队成绩的极差是30分；
（4）从平均分看，两队的平均分相同，实力大体相当；
从折线的走势看，甲队比赛成绩呈上升趋势，
而乙队比赛成绩呈下降趋势；
从获胜场数看，甲队胜三场，乙队胜两场，甲队成绩较好；
从极差看，甲队比赛成绩比乙队比赛成绩波动小，甲队成绩较稳定．
综上，选派甲队参赛更能取得好成绩．
25.D
E
B
A
C
（6分）
解：过点作于．
，∴
∴
在中，，
，
在中，
∴
∴（米）．∴雕塑的高度约为6.8米．
（8分）
解：（1）∵DC⊥OA，OC为半径． ∴DC为⊙O的切线
∵AB为⊙O的切线,B是切点 ∴DC=DB
在Rt△ACD中
∵ sinA=，BD：AD=1：2 ∴sinA= ∴∠A=30°∴tanA=
（2）连结OB
∵AB是⊙O的切线 ∴OB⊥AB
在Rt△AOB中
∵ tanA= OB=OC=1 ∴ AB=
∵∠A=30° ∴∠AOB=60° ∴的长是：=
27.（9分）
解：⑴由题意得，
R1=P(Q1－20)=(－2x＋80)[( EQ \F(1,2)x＋30)－20] =－x2＋20x＋800．(1≤x≤20，且x为整数)；
R2=P(Q2－20)=(－2x＋80)(45－20) =－50x＋2000．(21≤x≤30，且x为整数)；
⑵当1≤x≤20且x为整数时，R1=－（x－10）2＋900，
当x=10时，R1有最大值900，
当21≤x≤30且x为整数时， R2=－50x＋2000，R2的值随x的增大而减小，
故x=21时，R2有最大值950，
所以当x=21，即在第21天时，日销售利润最大，最大值是950元．
28．（10分）
解：（1）由题意知 ∠COB = 90°，B(8，0) ，OB=8
在Rt△OBC中tan∠ABC = OC= OB×tan∠ABC = 8×=4 ∴C(0,4)
∵ ∴AB = 4 A(4,0)
O
F
A
P
C
E
B
把A、B、C三点的坐标带入得
解得
所以抛物线的解析式为。
（2）C ( 0, 4 ) B ( 8, 0 ) E ( 0, 4-t ) ( t > 0)
OC = 4 ， OB = 8， CE = t ， BP=2t ， OP =8-2t
∵EF // OB∴△CEF ～△COB ∴ 则有 得 EF = 2t
=当t=2时 有最大值2.
（3）存在符合条件的t值，使△PBF与△ABC相似。
C ( 0, 4 ) B ( 8, 0 ) E ( 0, 4-t ) F(2t , 4 - t ) P ( 8-2t , 0 ) ( t > 0)
AB = 4 BP=2t BF = ∵ OC = 4 OB = 8 ∴BC =
①当点P与A、F与C对应 则，代入得 解得
②当点P与C、F与A对应 则，代入得 解得
综上所述：符合条件的和。

A.
B.
C.
D.
2
题次
1
2
3
4
5
6
7
8
9
10
答案
C
D
A
D
D
D
C
D
A
D