2024天水一中高二下学期4月月考试题数学含解析

这是一份2024天水一中高二下学期4月月考试题数学含解析，共9页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

命题：王亚丽、赵小军审核：赵小军
（满分：150分时间：120分钟）
一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．
1．在空间直角坐标系中，点关于平面对称的点为（ ）
A．B．C．D．
2．若函数在处的导数等于，则的值为（ ）
A．B．C．D．
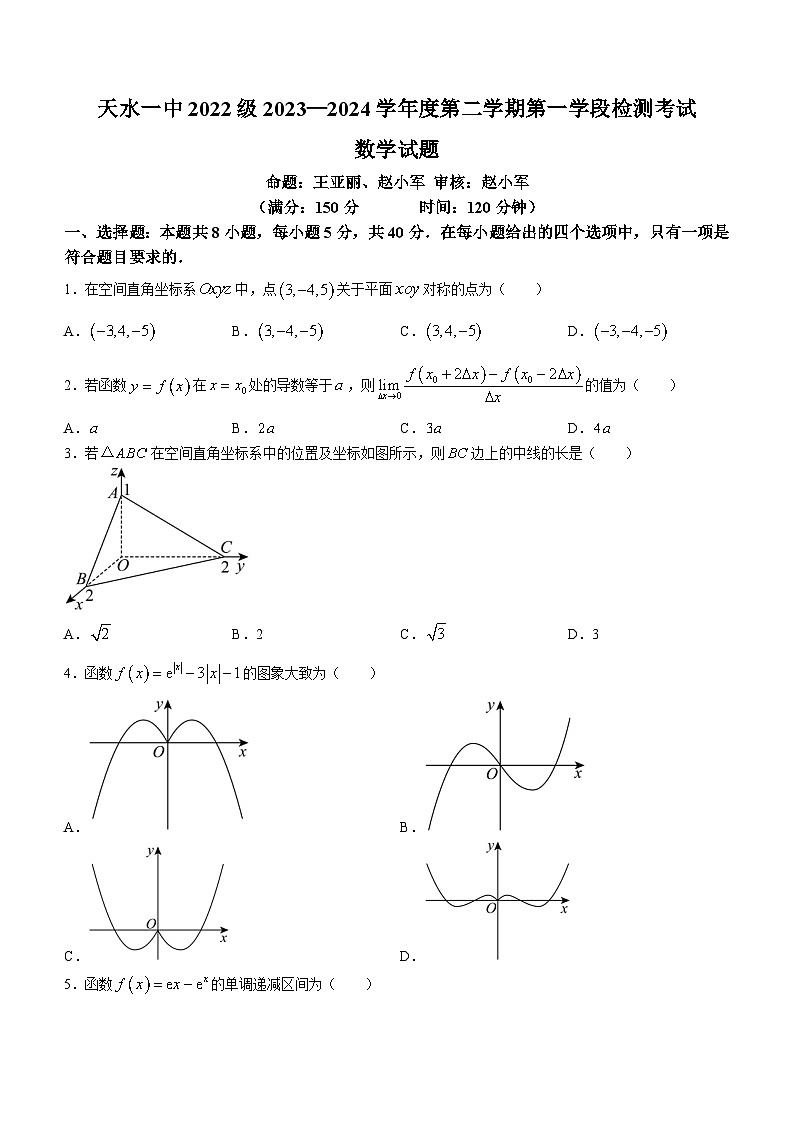
3．若在空间直角坐标系中的位置及坐标如图所示，则边上的中线的长是（ ）
A．B．2C．D．3
4．函数的图象大致为（ ）
A．B．
C．D．
5．函数的单调递减区间为（ ）
A．B．C．D．
6．如图1，现有一个底面直径为高为的圆锥容器，以的速度向该容器内注入溶液，随着时间（单位：s）的增加，圆锥容器内的液体高度也跟着增加，如图2所示，忽略容器的厚度，则当时，圆锥容器内的液体高度的瞬时变化率为（ ）
图1 图2
A．B．C．D．
7．已知，则大小关系为（ ）
A．B．C．D．
8．若对任意的，且，都有成立，则的最大值为（ ）
A．B．1C．eD．
二、选择题：本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求．全部选对的得6分，部分选对的得部分分，有选错的得0分．
9．已知向量，则下列结论正确的是（ ）
A．B．
C．D．
10．定义在R上的可导函数的导函数的图象如图所示，则下列结论正确的是（ ）
A．是函数的极大值点，是函数的极小值点
B．0是函数的极小值点
C．函数的单调递增区间是
D．函数的单调递减区间是
11．已知函数存在个不同的正数，使得，则下列说法正确的是（ ）
A．的最大值为5B．的最大值为4
C．的最大值为D．的最大值为
三、填空题：本题共3小题，每小题5分，共15分．
12．已知向量，若，则______．
13．对R上可导的函数，若满足，且，则的解集是______．
14．已知定义域为R的函数，对，若存在，对任意的，有恒成立，则称为函数的“特异点”．函数在其定义域上的“特异点”个数是______个．
四、解答题：本题共5小题，共77分．解答应写出文字说明、证明过程或演算步骤．
15．（本小题13分）如图，已知平行六面体中，底面是边长为1的正方形，．
（1）求线段的长度；
（2）求异面直线与所成角的余弦值．
16．（本小题15分）已知函数，且．
（1）求的值；
（2）设，求过点的切线方程．
17．（本小题15分）已知函数．
（1）求证：当时，曲线与直线只有一个交点；
（2）若既存在极大值，又存在极小值，求实数的取值范围．
18．（本小题17分）二十大报告中提出：全面推进乡村振兴，坚持农业农村优先发展．小王大学毕业后决定利用所学专业回乡自主创业，生产某农副产品．经过市场调研，生产该产品需投入年固定成本4万元，每生产万件，需另投入流动成本万元．已知在年产量不足6万件时，，在年产量不小于6万件时，．每件产品售价8元．通过市场分析，小王生产的产品当年能全部售完．
（1）写出年利润（万元）关于年产量（万件）的函数解析式．（年利润=年销售收入-年固定成本-流动成本）
（2）年产量为多少万件时，小王在这一产品的生产中所获年利润最大？最大年利润是多少？
19．（本小题17分）若时，函数取得极大值或极小值，则称为函数的极值点．已知函数，其中为正实数．
（1）若函数有极值点，求的取值范围；
（2）当和的几何平均数为，算术平均数为．
①判断与和的几何平均数和算术平均数的大小关系，并加以证明；
②当时，证明：．
天水一中2022级2023—2024学年度第二学期第一学段检测考试
数学试题答案
一、选择题：本题共8小题，每小题5分，共40分．
1．【答案】B 2．【答案】D 3．【答案】C 4．【答案】C 5．【答案】A
6．【答案】设注入溶液的时间为（单位：）时，溶液的高为，
则，得．
因为，
所以当时，，
即圆锥容器内的液体高度的瞬时变化率为．故选：C
7．【答案】D 8．【答案】A
二、选择题：本题共3小题，每小题6分，共18分．
9．【答案】AC 10．【答案】BC 11．【答案】BD
三、填空题：本题共3小题，每小题5分，共15分．
12．【答案】 13．【答案】：
14．【答案】：1
由题意知“特异点”为的极大值点，
因为，所以，
当时，，
当时，，
又，
，
故不存在．
又因为，
易知：当时，单调递增，故不可能有“特异点”，
当时，设，则，
令，则，则；
所以在上单调递增，在上单调递减，
故为的极大值点，即为的“特异点”．
综上所述，在其定义域内仅有一个“特异点”．
故答案为：1．
四、解答题：本题共5小题，共77分．
15、【解析】（1）设，则，
又，则．
（2）由，则，
则．
，
故异面直线与所成角的余弦值为．
16．【解析】（1）定义域为，
而，而已知，可得，
解得，故的值为1，
（2），设切点为，设切线斜率为，
而，故切线方程为，
将代入方程中，可得，解得（负根舍去），
故切线方程为，
17．【解析】（1）当时，函数，求导得：，
令，得；令，得；
则函数在上递增，在上递减，
故，
所以曲线与直线只有一个交点．
（2）函数的定义域为，
求导得，
设，
令，解得．
因为既存在极大值，又存在极小值，即在有两个变号零点，
则，解得且，
综上所述：的取值范围为．
18．【解析】（1）由题意，当时，，
当时，．
所以．
（2）当时，，令，解得．
当，当；
则在上单调递增，在上单调递减，
所以当时，．
当时，，当且仅当，即时取等号．
综上，当年产量为8万件时，所获年利润最大，为9万元．
19．【解析】（1）在上有变号零点，
即在上有变号零点．
①若，即时，只需矛盾，
②若，即时，只需故的取值范围为．
（2）①，
先证右边，证，令
证：，令，
，
在上单调递增，
再证左边证：，令证令
在上单调递减，，证毕！
②时，关于单调递减
设，
当时，；
当时，，
在上单调递增，上单调递减，，
所以当时，．