人教A版 (2019)必修 第一册第五章 三角函数5.5 三角恒等变换第2课时课后测评

这是一份人教A版 (2019)必修 第一册第五章 三角函数5.5 三角恒等变换第2课时课后测评，文件包含人教A版高中数学必修第一册同步讲义第41讲551两角和与差的正弦余弦和正切公式第2课时二倍角的正弦余弦正切公式原卷版doc、人教A版高中数学必修第一册同步讲义第41讲551两角和与差的正弦余弦和正切公式第2课时二倍角的正弦余弦正切公式教师版doc等2份试卷配套教学资源，其中试卷共34页， 欢迎下载使用。

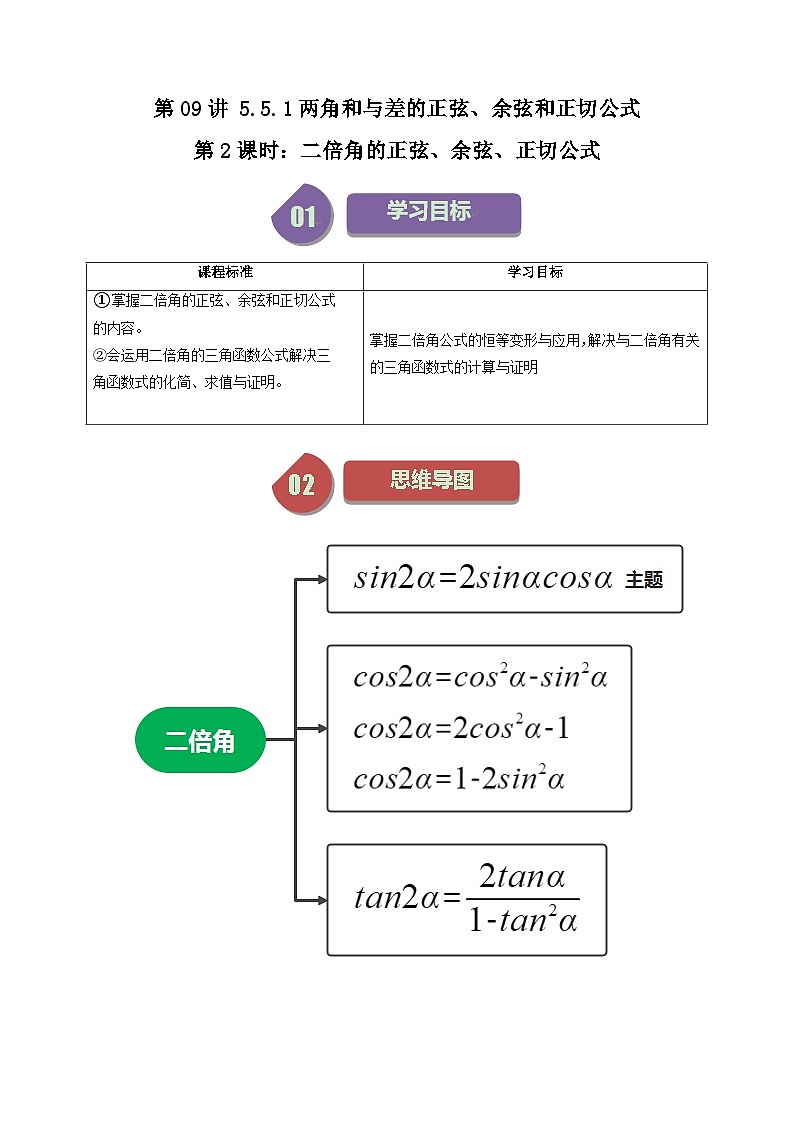
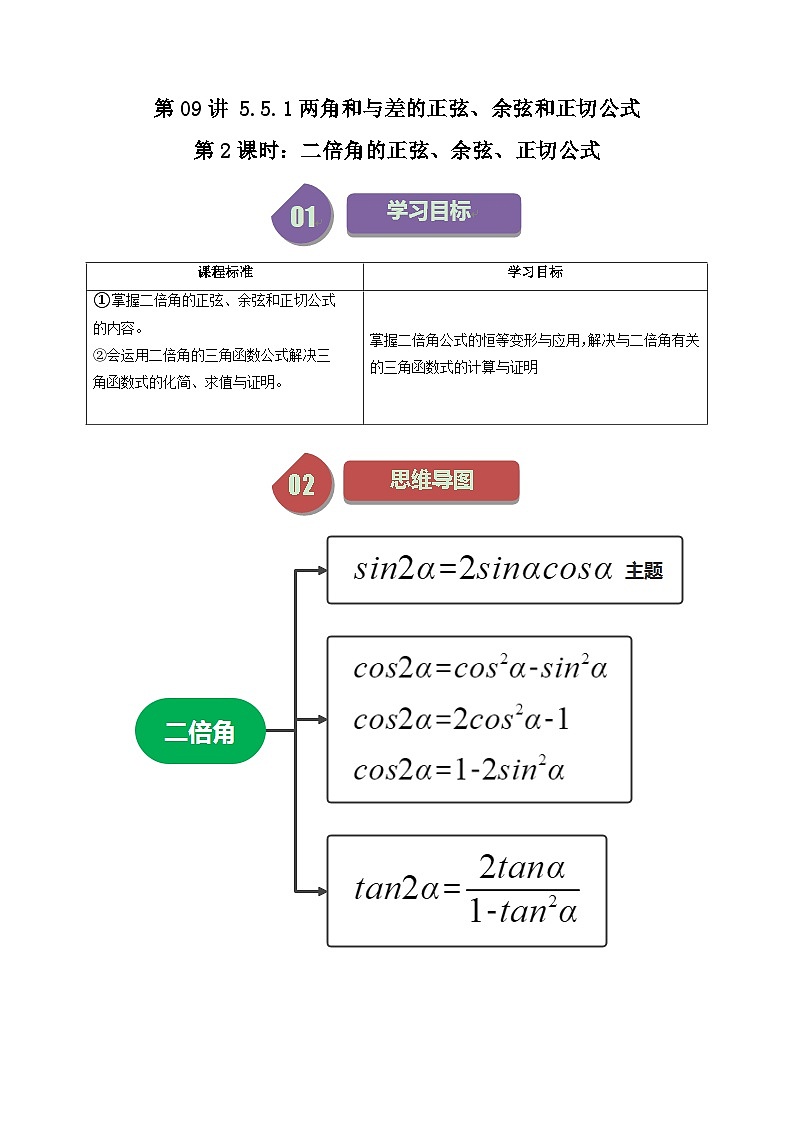
知识点01：二倍角的正弦、余弦正切公式
① SKIPIF 1 < 0
② SKIPIF 1 < 0 ； SKIPIF 1 < 0 ； SKIPIF 1 < 0
③ SKIPIF 1 < 0
【即学即练1】（2023春·海南省直辖县级单位·高一校考期中） SKIPIF 1 < 0 .
【答案】 SKIPIF 1 < 0 / SKIPIF 1 < 0
【详解】 SKIPIF 1 < 0 .
故答案为： SKIPIF 1 < 0
【即学即练2】（2023秋·高一课时练习） SKIPIF 1 < 0 SKIPIF 1 < 0 的值为 ．
【答案】 SKIPIF 1 < 0 / SKIPIF 1 < 0
【详解】原式 SKIPIF 1 < 0 .
故答案为： SKIPIF 1 < 0 .
【即学即练3】（2023·全国·高一随堂练习）若 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ．
【答案】 SKIPIF 1 < 0 / SKIPIF 1 < 0
【详解】因为 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 .
故答案为： SKIPIF 1 < 0
知识点02：降幂公式
① SKIPIF 1 < 0
② SKIPIF 1 < 0
【即学即练4】（2023春·山东泰安·高一校考阶段练习） SKIPIF 1 < 0 的值是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】D
【详解】 SKIPIF 1 < 0 .
故选：D.
【即学即练5】（2023春·广东佛山·高一校考阶段练习）函数 SKIPIF 1 < 0 的最小正周期等于 .
【答案】 SKIPIF 1 < 0
【详解】因为函数 SKIPIF 1 < 0
故最小正周期等于 SKIPIF 1 < 0 .
故答案为： SKIPIF 1 < 0
题型01 利用二倍角公式解决给角求值问题
【典例1】（2023秋·河南·高三校联考阶段练习）已知函数 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 （ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】A
【详解】 SKIPIF 1 < 0 ，
故 SKIPIF 1 < 0 ．
故选：A．
【典例2】（2023秋·宁夏银川·高三银川一中校考阶段练习）已知角 SKIPIF 1 < 0 的顶点为原点，始边为 SKIPIF 1 < 0 轴的非负半轴，若其终边经过点 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 .
【答案】 SKIPIF 1 < 0
【详解】由三角函数的定义可知， SKIPIF 1 < 0 ，
SKIPIF 1 < 0 .
故答案为： SKIPIF 1 < 0
【变式1】（2023秋·河南新乡·高三卫辉一中校联考阶段练习）已知角 SKIPIF 1 < 0 的终边过点 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 （ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】B
【详解】因为角 SKIPIF 1 < 0 的终边过点 SKIPIF 1 < 0 ，根据三角函数的定义，可得 SKIPIF 1 < 0 ，
则 SKIPIF 1 < 0 .
故选：B．
【变式2】（2023秋·广东湛江·高三校考阶段练习）已知角 SKIPIF 1 < 0 的终边与单位圆交于点 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0
【答案】 SKIPIF 1 < 0 / SKIPIF 1 < 0
【详解】因为角 SKIPIF 1 < 0 的终边与单位圆交于点 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 .
故答案为： SKIPIF 1 < 0
题型02利用二倍角公式求角
【典例1】（2023秋·福建厦门·高三厦门一中校考阶段练习）已知 SKIPIF 1 < 0 为锐角， SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 .
【答案】 SKIPIF 1 < 0
【详解】由于 SKIPIF 1 < 0 为锐角，所以 SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 .
故答案为： SKIPIF 1 < 0
【典例2】（2023秋·河南新乡·高一校联考期末）已知 SKIPIF 1 < 0 ，其中 SKIPIF 1 < 0 ．
(1)求 SKIPIF 1 < 0 ；
(2)求 SKIPIF 1 < 0 ．
【答案】(1) SKIPIF 1 < 0
(2) SKIPIF 1 < 0
【详解】（1）因为 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 ，
又因为 SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 ．
因为 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 ，
则 SKIPIF 1 < 0 SKIPIF 1 < 0 ，
又因为 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 ．
（2）由（1）可得 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
因为 SKIPIF 1 < 0 ，
则 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 SKIPIF 1 < 0
【变式1】（2023·全国·高三专题练习）已知 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 （ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 或 SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0 或 SKIPIF 1 < 0 或 SKIPIF 1 < 0
【答案】C
【详解】∵ SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 ，∴ SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，∴ SKIPIF 1 < 0 ．
∵ SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 ，∴ SKIPIF 1 < 0 ，∴ SKIPIF 1 < 0 ，
又 SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ．
答案：C.
【变式2】（2023秋·陕西西安·高三西安市铁一中学校考阶段练习）已知 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ．
【答案】 SKIPIF 1 < 0
【详解】因为 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
因为 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，因此 SKIPIF 1 < 0 ，
因为 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 ，
故答案为： SKIPIF 1 < 0
题型03利用二倍角公式解决条件求值问题
【典例1】（2023·山西运城·高三校考学业考试）已知 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 （ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】B
【详解】由 SKIPIF 1 < 0 得， SKIPIF 1 < 0 ，
而 SKIPIF 1 < 0 ，
故 SKIPIF 1 < 0
SKIPIF 1 < 0 ，
故选：B
【典例2】（2023秋·福建三明·高三三明一中校考阶段练习）已知 SKIPIF 1 < 0 ， SKIPIF 1 < 0 均为锐角， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ， SKIPIF 1 < 0 .
【答案】 SKIPIF 1 < 0 SKIPIF 1 < 0
【详解】因为 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 ，
又因 SKIPIF 1 < 0 ， SKIPIF 1 < 0 均为锐角，所以 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
又因 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 ，
则 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 .
故答案为： SKIPIF 1 < 0 ； SKIPIF 1 < 0 .
【变式1】（2023秋·河南新乡·高一校联考期末）若 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 （ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】C
【详解】由 SKIPIF 1 < 0 ，得 SKIPIF 1 < 0 ，
则 SKIPIF 1 < 0 ．
故选：C
【变式2】（2023·云南·校联考模拟预测）在 SKIPIF 1 < 0 中，若 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ．
【答案】 SKIPIF 1 < 0 /0.96
【详解】 SKIPIF 1 < 0 ，
因为 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 .
故答案为： SKIPIF 1 < 0
【变式3】（2023·全国·高一课堂例题）已知 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，求 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 的值．
【答案】 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ．
【详解】因为 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 ．
所以 SKIPIF 1 < 0 ．
所以 SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ．
题型04二倍角中的拼凑角问题
【典例1】（2023秋·山东德州·高三德州市第一中学校考阶段练习）已知 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 （ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】C
【详解】 SKIPIF 1 < 0
SKIPIF 1 < 0 ，
故选：C
【典例2】（2023·四川绵阳·盐亭中学校考模拟预测）已知 SKIPIF 1 < 0 ​，则 SKIPIF 1 < 0 ​ ．
【答案】 SKIPIF 1 < 0 /0.28
【详解】由题意， SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
解得： SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
故答案为： SKIPIF 1 < 0 .
【典例3】（2023春·山东青岛·高一校联考期中）已知 SKIPIF 1 < 0 为锐角， SKIPIF 1 < 0 ．
(1)求 SKIPIF 1 < 0 的值；
(2)求 SKIPIF 1 < 0 的值．
【答案】(1) SKIPIF 1 < 0
(2) SKIPIF 1 < 0
【详解】（1）因为 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0
（2）因为 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 ，
因为 SKIPIF 1 < 0 为锐角，所以 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 ，
则 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0
【变式1】（2023秋·重庆沙坪坝·高三重庆一中校考阶段练习）已知 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 （ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】C
【详解】 SKIPIF 1 < 0 SKIPIF 1 < 0 ，
故选：C.
【变式2】（2023春·江苏连云港·高一校考阶段练习）已知 SKIPIF 1 < 0 是第一象限角，满足 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 （ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】B
【详解】因为 SKIPIF 1 < 0 是第一象限，则 SKIPIF 1 < 0 为第一象限角或第二象限角，
且 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 ，
由题意可得： SKIPIF 1 < 0 .
故选：B.
【变式3】（2023秋·河北邢台·高三校联考阶段练习）已知 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ．
【答案】 SKIPIF 1 < 0
【详解】 SKIPIF 1 < 0 ．
故答案为： SKIPIF 1 < 0 .
题型05二倍角公式与数学文化的结合
【典例1】（2023秋·河南·高三校联考阶段练习）我国古代数学家僧一行应用“九服晷影算法”在《大衍历》中建立了影长 SKIPIF 1 < 0 与太阳天顶距 SKIPIF 1 < 0 的对应数表，这是世界数学史上较早的正切函数表．根据三角学知识可知，晷影长 SKIPIF 1 < 0 等于表高 SKIPIF 1 < 0 与太阳天顶距 SKIPIF 1 < 0 正切值的乘积，即 SKIPIF 1 < 0 ．对同一“表高”测量两次，第一次和第二次太阳天顶距分别为 SKIPIF 1 < 0 ，若第一次的“晷影长”是“表高”的2倍，第二次的“晷影长”是“表高”的4倍，则 SKIPIF 1 < 0 （ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】D
【详解】由第一次的“晷影长”是“表高”的2倍，得 SKIPIF 1 < 0 ，
由第二次的“晷影长”是“表高”的4倍，得 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 SKIPIF 1 < 0 ．
故选：D
【典例2】（2023秋·山东威海·高三校考阶段练习）黄金比又称黄金律，是指事物各部分间一定的数学比例关系，即将整体一分为二，较小部分与较大部分之比等于较大部分与整体之比，其比值为 SKIPIF 1 < 0 ，上述比例又被称为黄金分割．将底和腰之比等于 SKIPIF 1 < 0 的等腰三角形称为黄金三角形，若某黄金三角形的一个底角为C，则 SKIPIF 1 < 0 ．
【答案】 SKIPIF 1 < 0
【详解】
设这个黄金三角形的另一个底角为B，顶角为A，
因为 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 ，
则 SKIPIF 1 < 0 ．
故答案为： SKIPIF 1 < 0 .
【变式1】（2023春·广东揭阳·高二校联考期中）五角星是非常美丽的，我们的国旗上就有五颗，还有不少国家的国旗也用五角星，因为在五角星中可以找到许多线段之间的长度关系是符合黄金分割比的，也就是说正五边形对角线连满后出现的所有三角形，都是黄金分割三角形.如图所示的五角星中 SKIPIF 1 < 0 、 SKIPIF 1 < 0 、 SKIPIF 1 < 0 等都是黄金分割比 SKIPIF 1 < 0 ，已知五角星的顶角是36°，则利用上面信息可求得 SKIPIF 1 < 0 （ ）

A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】C
【详解】由图形可知 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 ，
故选：C
【变式2】（2023春·福建漳州·高一漳州三中校考期中）黄金分割蕴藏着丰富的数学知识和美学价值，被广泛运用于艺术创作、工艺设计等领域，黄金分割的比值为无理数 SKIPIF 1 < 0 该值恰好等于 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 （ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】C
【详解】由题意 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
故选：C．
A夯实基础 B能力提升
A夯实基础
一、单选题
1．（2023秋·北京·高三统考开学考试）已知函数 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 的值为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D．1
【答案】B
【详解】 SKIPIF 1 < 0 .
故选：B
2．（2023春·甘肃陇南·高一统考期末） SKIPIF 1 < 0 （ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】D
【详解】 SKIPIF 1 < 0 .
故选：D
3．（2023春·江苏镇江·高一扬中市第二高级中学校考期中）函数 SKIPIF 1 < 0 的最小正周期是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】C
【详解】因为 SKIPIF 1 < 0 ，
所以所求最小正周期为 SKIPIF 1 < 0 .
故选：C.
4．（2023秋·湖南衡阳·高三衡阳市八中校考开学考试）已知 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 （ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】B
【详解】由 SKIPIF 1 < 0 ，有 SKIPIF 1 < 0 ，得 SKIPIF 1 < 0 ，
可得 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 .故A，C，D错误.
故选：B.
5．（2023秋·河北张家口·高三统考开学考试）已知 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 的值为（ ）．
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】C
【详解】由题意得， SKIPIF 1 < 0 ，
解得 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 ．
故选：C
6．（2023·贵州·校联考模拟预测）若 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 （ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】C
【详解】∵ SKIPIF 1 < 0 ，∴ SKIPIF 1 < 0
∴ SKIPIF 1 < 0 .
故选：C.
7．（2023·福建厦门·厦门一中校考模拟预测）已知角 SKIPIF 1 < 0 的终边落在直线 SKIPIF 1 < 0 上，则 SKIPIF 1 < 0 的值为（ ）
A． SKIPIF 1 < 0 B．1C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】B
【详解】因为角 SKIPIF 1 < 0 的终边落在直线 SKIPIF 1 < 0 上，所以 SKIPIF 1 < 0 .
则 SKIPIF 1 < 0 SKIPIF 1 < 0 SKIPIF 1 < 0 .
故选：B
8．（2023秋·山东威海·高三校考阶段练习）已知 SKIPIF 1 < 0 和 SKIPIF 1 < 0 是关于 SKIPIF 1 < 0 的方程 SKIPIF 1 < 0 的两根，且 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 的值为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】B
【详解】因为 SKIPIF 1 < 0 和 SKIPIF 1 < 0 是关于 SKIPIF 1 < 0 的方程 SKIPIF 1 < 0 的两根，
所以 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 ，
因为 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
故选：B
二、多选题
9．（2023春·四川宜宾·高一校考期中）下列各式中，值为 SKIPIF 1 < 0 的是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】ACD
【详解】对于A， SKIPIF 1 < 0 ，故A正确；
对于B， SKIPIF 1 < 0 ，故B错误；
对于C， SKIPIF 1 < 0 ，故C正确；
对于D， SKIPIF 1 < 0 ，故D正确；
故选：ACD
10．（2023春·四川绵阳·高一校考阶段练习）下列各式中，值为 SKIPIF 1 < 0 的是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】AD
【详解】对于A， SKIPIF 1 < 0 ，A正确；
对于B， SKIPIF 1 < 0 ，B错误；
对于C， SKIPIF 1 < 0 ，C错误；
对于D， SKIPIF 1 < 0 ，D正确．
故选：AD
三、填空题
11．（2023春·浙江杭州·高三浙江省杭州第二中学校考阶段练习）已知 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 .
【答案】 SKIPIF 1 < 0
【详解】由题意 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
又因为 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 .
故答案为： SKIPIF 1 < 0 .
12．（2023春·甘肃天水·高一天水市第一中学校考期中）已知 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 的值域为 .
【答案】 SKIPIF 1 < 0
【详解】根据题意，令 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，
因为 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 ，
因此 SKIPIF 1 < 0 ，
因为 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 ，故函数值域为 SKIPIF 1 < 0 .
故答案为： SKIPIF 1 < 0 .
四、解答题
13．（2023·全国·高一随堂练习）求下列各式的值：
(1) SKIPIF 1 < 0 ；
(2) SKIPIF 1 < 0 ；
(3) SKIPIF 1 < 0 .
【答案】(1) SKIPIF 1 < 0
(2) SKIPIF 1 < 0
(3) SKIPIF 1 < 0
【详解】（1） SKIPIF 1 < 0
SKIPIF 1 < 0
（2） SKIPIF 1 < 0
SKIPIF 1 < 0
（3） SKIPIF 1 < 0 .
14．（2023秋·福建龙岩·高三上杭一中校考阶段练习）如图，在平面直角坐标系 SKIPIF 1 < 0 中，锐角 SKIPIF 1 < 0 和钝角 SKIPIF 1 < 0 的终边分别与单位圆交于A，B两点，且 SKIPIF 1 < 0 两点的横坐标分别为 SKIPIF 1 < 0 .
(1)求 SKIPIF 1 < 0 的值；
(2)求 SKIPIF 1 < 0 的值.
【答案】(1) SKIPIF 1 < 0 ；
(2) SKIPIF 1 < 0 .
【详解】（1）因为锐角 SKIPIF 1 < 0 和钝角 SKIPIF 1 < 0 的终边分别与单位圆交于点A，B，且点A，B的横坐标分别为 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
显然点A在第一象限，点B在第二象限，则点A，B的纵坐标分别为 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
由已知及三角函数定义得 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，而 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 .
（2）由（1）知 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 .
B能力提升
1．（2023秋·江苏扬州·高三扬州中学校考阶段练习）已知 SKIPIF 1 < 0 为锐角，若 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 的值为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】D
【详解】 SKIPIF 1 < 0 为锐角， SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 ．
故 SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
故选：D．
2．（2023春·陕西榆林·高二校考阶段练习） SKIPIF 1 < 0 等于（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D．2
【答案】A
【详解】 SKIPIF 1 < 0 ．
故选：A．
3．（2023秋·四川泸州·高三泸州老窖天府中学校考阶段练习）已知 SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 的值为 ．
【答案】 SKIPIF 1 < 0 ./0.96
【详解】由 SKIPIF 1 < 0 可得 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 ，
由二倍角公式及诱导公式可得
SKIPIF 1 < 0 .
故答案为： SKIPIF 1 < 0 .
4．（2023秋·安徽铜陵·高三统考阶段练习）已知 SKIPIF 1 < 0 ．
(1)求 SKIPIF 1 < 0 的值；
(2)求 SKIPIF 1 < 0 的值．
【答案】(1) SKIPIF 1 < 0
(2) SKIPIF 1 < 0
【详解】（1）解：∵ SKIPIF 1 < 0 ，
∴解得： SKIPIF 1 < 0 .
（2）解：由（1）知 SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
SKIPIF 1 < 0 .
又∵ SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0 .
即得： SKIPIF 1 < 0 .
5．（2023秋·河南南阳·高三校联考阶段练习）已知 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ．
(1)求 SKIPIF 1 < 0 的值；
(2)若 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，求 SKIPIF 1 < 0 的值．
【答案】(1) SKIPIF 1 < 0
(2) SKIPIF 1 < 0
【详解】（1）因为 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 ，
又 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 ．
所以 SKIPIF 1 < 0 ．
（2）由（1），得 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
又 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 ，又 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ．
所以 SKIPIF 1 < 0
SKIPIF 1 < 0 .
课程标准
学习目标
①掌握二倍角的正弦、余弦和正切公式
的内容。
②会运用二倍角的三角函数公式解决三
角函数式的化简、求值与证明。
掌握二倍角公式的恒等变形与应用，解决与二倍角有关的三角函数式的计算与证明