第4章 三角形 北师大版数学七年级下素养综合检测(含解析)

这是一份第4章 三角形 北师大版数学七年级下素养综合检测(含解析)，共15页。

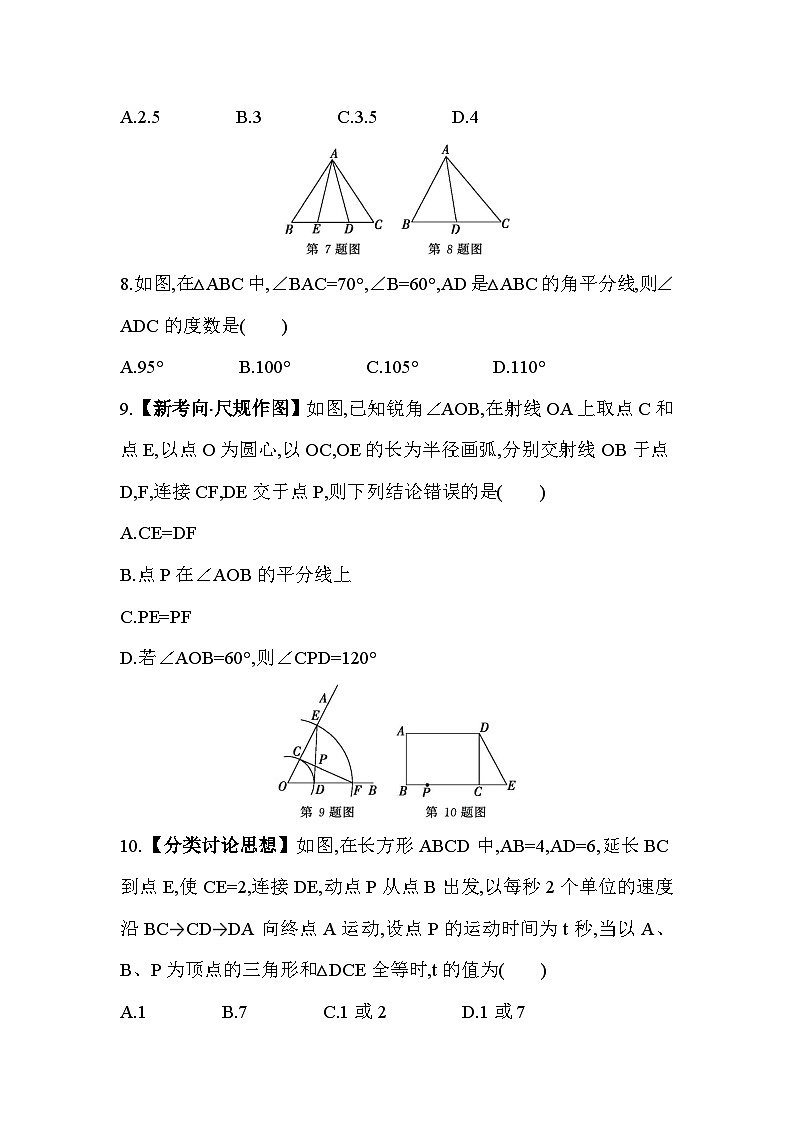
第四章　素养综合检测(满分100分,限时60分钟)一、选择题(共10小题,每小题3分,共30分)1.在下列各图的△ABC中,正确画出AC边上的高的图形是(　　)　　　　　　　　　　　　　　　　2.下列说法正确的是(　　)A.三角形的三条中线交于一点B.三角形的角平分线是射线C.三角形的高所在的直线交于一点,这一点不在三角形内就在三角形外D.三角形的一条角平分线把三角形分成两个面积相等的三角形3.如图所示,一扇窗户打开后,用窗钩AB即可固定,这里所用的数学道理是(　　)A.两定确定一条直线　　　　　　B.两点之间线段最短C.三角形的稳定性　　　　　　D.垂线段最短　4.一个三角形的三边长之比是2∶2∶1,周长是10,则这个三角形按边分是(　　)A.等腰三角形　　　　　　B.等边三角形C.不等边三角形　　　　　　D.以上都不对5.如图,在5×5的正方形网格中,△ABC的三个顶点都在格点上,则与△ABC有一条公共边且全等(不与△ABC重合)的格点三角形(顶点都在格点上的三角形)共有(　　)A.5个　　　　B.6个　　　　C.7个　　　　D.8个6.如图1,a,b,c分别表示△ABC的三边长,则图2中与△ABC一定全等的三角形是(　　)　　　A.①　　　　B.②　　　　C.③　　　　D.④7.如图,△ABC中,BC=10,点D、E在BC上,DE=4,若△ABD≌△ACE,则BE=(　　)A.2.5　　　　B.3　　　　C.3.5　　　　D.4　8.如图,在△ABC中,∠BAC=70°,∠B=60°,AD是△ABC的角平分线,则∠ADC的度数是(　　)A.95°　　　　B.100°　　　　C.105°　　　　D.110°9.【新考向·尺规作图】如图,已知锐角∠AOB,在射线OA上取点C和点E,以点O为圆心,以OC,OE的长为半径画弧,分别交射线OB于点D,F,连接CF,DE交于点P,则下列结论错误的是(　　)A.CE=DFB.点P在∠AOB的平分线上C.PE=PFD.若∠AOB=60°,则∠CPD=120°　10.【分类讨论思想】如图,在长方形ABCD中,AB=4,AD=6,延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC→CD→DA向终点A运动,设点P的运动时间为t秒,当以A、B、P为顶点的三角形和△DCE全等时,t的值为(　　)A.1　　　　B.7　　　　C.1或2　　　　D.1或7二、填空题(共6小题,每小题3分,共18分)11.(2023湖北咸宁期中)如图,有一个与地面成30°角的斜坡,现要在斜坡上竖一电线杆,当电线杆与地面垂直时,它与斜坡所成的夹角α=　　　　°. 　12.(2023重庆渝中期中)如图,AB⊥CD,且AB=CD,E,F是AD上两点,CE⊥AD,BF⊥AD.若CE=8,BF=5,EF=4,则AD的长为　　　　. 13.【新考向·代数推理】△ABC的三边长分别是a,b,c,化简|a-b+c|+|a-c-b|-|b-c-a|的结果为　　　　. 14.【对称模型】(2023广东深圳南山期中)如图,已知∠CAE=∠DAB,AC=AD.给出下列条件:①AB=AE;②BC=ED;③∠C=∠D;④∠B=∠E.其中能使△ABC≌△AED的条件为　　　　.(填序号) 15.【生命安全与健康】某段河流的两岸是平行的,数学兴趣小组想测得河的宽度,为了保证安全,在老师带领下不用涉水过河就可以测量,他们是这样做的:①在河流的一条岸边B点,选对岸正对的一棵树A;②沿河岸直走20米有一棵树C,继续前行20米到达D处;③从D处沿河岸垂直的方向行走,当到达树A正好被树C遮挡住的E处时停止行走;④测得DE的长为5米.则河的宽度为　　　　米. 16.(2023河南信阳潢川期末)如图,△ABC的两条中线AM,BN相交于点O,已知△ABO的面积为4,△BOM的面积为2,则四边形MCNO的面积为　　　　. 三、解答题(共5小题,共52分)17.【教材变式·P96T6】(10分)沿着图中的虚线,将图形分割成四个全等的图形.18.【新独家原创】(10分)如图,已知AD,AE分别是△ABC的高和中线,∠CAB=90°.(1)若AB=3,AD=2.4,BC=5,求AC的长;(2)若AC-AB=5,且△AEC的周长是15,求△ABE的周长.19.【爱国主义教育】(10分)杨阳同学沿一段笔直的人行道行走,在由A步行到达B处的过程中,通过隔离带的空隙O,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语.其具体信息如下:如图,AB∥OH∥CD,相邻两平行线间的距离相等,AC,BD相交于O,OD⊥CD,垂足为D.已知AB=20米.请根据信息求标语CD的长度.20.【动点问题】(10分)如图,△ABC中,AB=BC=CA,∠A=∠ABC=∠ACB,在△ABC的顶点A,C处各有一只小蚂蚁,它们同时出发,分别以相同速度由A向B和由C向A爬行,经过t(s)后,它们分别爬行到了D,E处,设DC与BE的交点为F.(1)△ACD≌△CBE吗?为什么?(2)小蚂蚁在爬行过程中,∠BFC的大小有没有变化?请说明理由.21.【项目式学习试题】(12分)(1)【问题背景】如图1,在四边形ABCD中,AB=AD,∠B+∠ADF=180°,E、F分别是线段BC、线段CD上的点.若∠BAD=2∠EAF,试探究线段BE、EF、FD之间的数量关系.童威同学探究此问题的方法是延长FD到点G,使DG=BE,连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是　　　　　　. (2)【猜想论证】如图2,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E在线段BC上,F在线段CD的延长线上.若∠BAD=2∠EAF,(1)中的结论是否仍然成立?若成立,请说明理由;若不成立,试写出相应的结论并给出证明.　答案全解全析1.C　在△ABC中,AC边上的高就是过B作BD⊥AC,交CA的延长线于点D,如图,线段BD即为所求.故选C.2.A　A.三角形的三条中线交于一点,故此选项说法正确;B.三角形的角平分线是线段,故此选项说法错误;C.三角形的高所在的直线交于一点,当三角形为锐角三角形时,交点在三角形的内部,当三角形为直角三角形时,交点在直角顶点上,当三角形为钝角三角形时,交点在三角形的外部,故此选项说法错误;D.三角形的一条中线把三角形分成两个面积相等的三角形,故此选项说法错误.故选A.3.C　4.A　由题意可知这个三角形的三边长分别为10×25=4,10×25=4,10×15=2,∴这个三角形按边分是等腰三角形.故选A.5.B　如图所示:以BC为公共边,可画出△BDC,△BEC,△BFC三个三角形和△ABC全等.以AB为公共边,可画出△ABG,△ABM,△ABH三个三角形和△ABC全等.以AC为公共边,不可以画出一个三角形和△ABC全等,所以可画出6个.故选B.6.B　180°-72°-50°=58°,题图②中的三角形与△ABC有两条边对应相等,且这两条边的夹角都为58°,∴题图②中的三角形与△ABC全等.故选B.7.B　∵△ABD≌△ACE,∴BD=CE,∴BD-DE=CE-DE,∴BE=CD,∵BC=10,DE=4,∴BE=12×(10-4)=3,故选B.8.A　∵AD是△ABC的角平分线,∠BAC=70°,∴∠BAD=35°,∵∠B=60°,∴∠ADB=180°-(∠B+∠BAD)=180°-(60°+35°)=85°,∴∠ADC=180°-85°=95°,故选A.9.D　A.由题意得OE=OF,OC=OD,∴OE-OC=OF-OD,∴CE=DF,∴A选项的结论正确;B.如图,连接OP,在△ODE和△OCF中,OE=OF,∠COD=∠COD,OD=OC,∴△ODE≌△OCF(SAS),∴∠OED=∠OFC,在△PCE和△PDF中,∠CPE=∠DPF,∠PEC=∠PFD,CE=DF,∴△PCE≌△PDF(AAS),∴PC=PD,在△OCP和△ODP中,OC=OD,OP=OP,PC=PD,∴△OCP≌△ODP(SSS),∴∠COP=∠DOP,∴点P在∠AOB的平分线上,∴B选项的结论正确;C.∵△PCE≌△PDF,∴PE=PF,∴C选项的结论正确;D.若∠AOB=60°,∵△OCP≌△ODP,∴∠OCP=∠ODP,∴当DE⊥OD,CF⊥OE时,才有∠CPD=120°,∴D选项的结论错误.故选D.10.D　∵四边形ABCD为长方形,∴AB=CD=4,AD=BC=6,∠ABP=∠DCE=∠BAD=90°,∵以A、B、P为顶点的三角形和△DCE全等,∴①点P在BC上,当BP=CE时,△ABP≌△DCE,此时BP=2t=2,∴t=1;②点P在CD上,不存在以A、B、P为顶点的三角形和△DCE全等;③点P在AD上,当AP=CE时,△BAP≌△DCE,此时AP=16-2t=2,解得t=7.综上所述,当t的值为1或7时,△ABP和△DCE全等.故选D.11.　答案　60解析　如图,延长BA与CD交于点E,∵BE⊥CD,∴∠1=90°-30°=60°,由对顶角相等,得α=∠1=60°.故答案为60.12.　答案　9解析　∵AB⊥CD,CE⊥AD,BF⊥AD,∴∠AFB=∠CED=90°,∠A+∠D=90°,∠C+∠D=90°,∴∠A=∠C,∵AB=CD,∴△ABF≌△CDE(AAS),∴AF=CE=8,BF=DE=5,∵EF=4,∴AD=AF+DF=8+(5-4)=9.13.　答案　b+c-a解析　∵a,b,c是△ABC的三边长,∴b+c>a,a+c>b,∴a-b+c>0,a-c-b<0,b-c-a<0,∴|a-b+c|+|a-c-b|-|b-c-a|=(a-b+c)-(a-c-b)+(b-c-a)=a-b+c-a+c+b+b-c-a=b+c-a.14.　答案　①③④解析　∵∠CAE=∠DAB,∴∠CAE+∠EAB=∠DAB+∠EAB,∴∠CAB=∠DAE,又AC=AD,∴①当AB=AE时,可通过SAS证明△ABC≌△AED;②当BC=ED时,不能证明△ABC≌△AED;③当∠C=∠D时,可通过ASA证明△ABC≌△AED;④当∠B=∠E时,可通过AAS证明△ABC≌△AED.故答案为①③④.15.　答案　5解析　在△ABC和△EDC中,∠ABC=∠EDC=90°,BC=DC,∠ACB=∠ECD,∴△ABC≌△EDC(ASA),∴AB=ED,∵DE=5米,∴AB=5米,即河的宽度是5米.16.　答案　4解析　∵AM和BN为△ABC的两条中线,△ABO的面积为4,△BOM的面积为2,∴S△BCN=S△ABM=4+2=6,∴S四边形MCNO=S△BCN-S△BOM=6-2=4.17.　解析　答案不唯一.如图所示:18.　解析　(1)∵∠CAB=90°,AD是BC边上的高, ∴12AB·AC=12BC·AD,∵AB=3,AD=2.4,BC=5,∴AC=4.(2)∵AE是BC边上的中线,∴BE=EC,∵△AEC的周长是15,∴AE+AC+EC=15,∵AC-AB=5,∴AE+AC+EC-5=AE+AB+BE=10,则△ABE的周长=AE+AB+BE=10.19.　解析　因为AB∥CD,所以∠ABO=∠CDO.因为OD⊥CD,所以∠CDO=90°,所以∠ABO=90°,即BO⊥AB.因为相邻两平行线间的距离相等,所以OD=OB.在△ABO与△CDO中,∠ABO=∠CDO,BO=DO,∠AOB=∠COD,所以△ABO≌△CDO.所以CD=AB=20(米).20.　解析　(1)△ACD≌△CBE.理由如下:由题意得AD=CE,∵AC=CB,∠A=∠BCE,∴△ACD≌△CBE(SAS).(2)小蚂蚁在爬行过程中,∠BFC的大小没有变化.理由:∵△ACD≌△CBE,∴∠EBC=∠DCA.∵∠DCA+∠BCD=60°,∴∠EBC+∠BCD=60°,∴∠BFC=180°-60°=120°.故小蚂蚁在爬行过程中,∠BFC的大小没有变化.21.　解析　(1)BE+FD=EF.[详解]∵∠B+∠ADF=180°,∠ADF+∠ADG=180°,∴∠B=∠ADG,又∵AB=AD,BE=GD,∴△ABE≌△ADG(SAS),∴∠BAE=∠DAG,AG=AE,∵∠BAD=2∠EAF,∴∠BAE+∠DAF=∠EAF,∴∠EAF=∠GAF,又∵AE=AG,AF=AF,∴△AEF≌△AGF(SAS),∴GF=FE,∴GD+DF=GF=EF,∵BE=GD,∴BE+FD=EF.(2)(1)中的结论不成立,结论应是EF+FD=BE.证明:如图所示,在BC上截取BG=DF,连接AG.∵∠B+∠ADC=180°,∠ADF+∠ADC=180°,∴∠B=∠ADF.又∵AB=AD,BG=DF,∴△ABG≌△ADF(SAS),∴∠BAG=∠DAF,AG=AF,∴∠DAF+∠DAE=∠BAG+∠EAD=12∠BAD,∴∠EAG=12∠BAD,∴∠EAG=∠EAF,又∵AG=AF,AE=AE,∴△GAE≌△FAE,∴GE=FE,∴EF+FD=GE+BG=BE.