数学八年级下册第9章 中心对称图形——平行四边形9.3 平行四边形精练

这是一份数学八年级下册第9章 中心对称图形——平行四边形9.3 平行四边形精练，文件包含专题09解题技巧专题特殊平行四边形中定值最值问题压轴题三种模型全攻略原卷版docx、专题09解题技巧专题特殊平行四边形中定值最值问题压轴题三种模型全攻略解析版docx等2份试卷配套教学资源，其中试卷共42页， 欢迎下载使用。
目录
TOC \ "1-3" \h \u \l "_Tc22918" 【典型例题】 PAGEREF _Tc22918 \h 1
\l "_Tc14349" 【考点一 定值问题】 PAGEREF _Tc14349 \h 1
\l "_Tc26422" 【考点二 最小值问题】 PAGEREF _Tc26422 \h 8
\l "_Tc10995" 【考点三 最大值问题】 PAGEREF _Tc10995 \h 22
【典型例题】
【考点一 定值问题】
例题：（2022秋·山东枣庄·九年级校考阶段练习）如图，在矩形中，，，是上异于和的任意一点，且于，于，则为_____．
【变式训练】
1．（2023秋·吉林长春·八年级长春外国语学校校考期末）如图，菱形的周长为20，面积为24，是对角线上一点，分别作点到直线、的垂线段、，则等于______
2．（2020秋·辽宁沈阳·九年级统考期末）如图，在菱形中，是对角线上一动点，过点作于点，于点．若菱形的周长为20，面积为24，则的值为______．
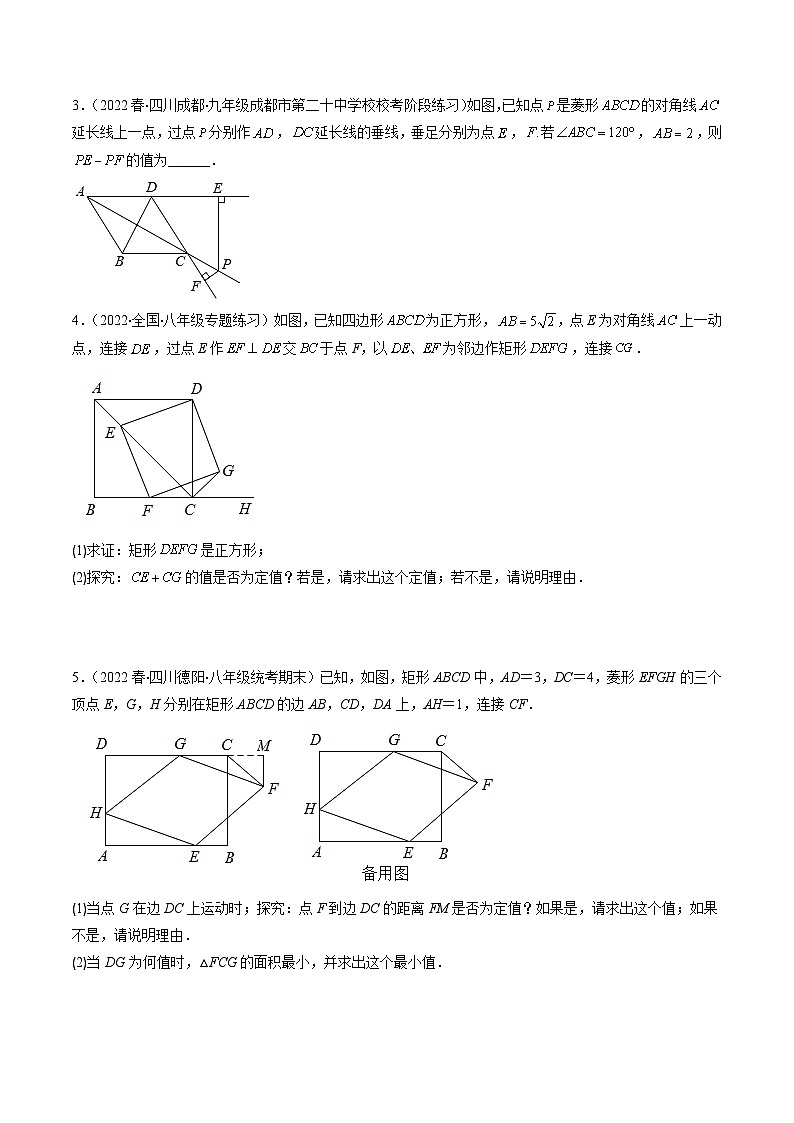
3．（2022春·四川成都·九年级成都市第二十中学校校考阶段练习）如图，已知点是菱形的对角线延长线上一点，过点分别作，延长线的垂线，垂足分别为点，若，，则的值为______．
4．（2022·全国·八年级专题练习）如图，已知四边形为正方形，，点E为对角线上一动点，连接，过点E作交于点F，以为邻边作矩形，连接．
(1)求证：矩形是正方形；
(2)探究：的值是否为定值？若是，请求出这个定值；若不是，请说明理由．
5．（2022春·四川德阳·八年级统考期末）已知，如图，矩形ABCD中，AD＝3，DC＝4，菱形EFGH的三个顶点E，G，H分别在矩形ABCD的边AB，CD，DA上，AH＝1，连接CF．
(1)当点G在边DC上运动时；探究：点F到边DC的距离FM是否为定值？如果是，请求出这个值；如果不是，请说明理由．
(2)当DG为何值时，△FCG的面积最小，并求出这个最小值．
【考点二 最小值问题】
例题：（2022秋·重庆沙坪坝·八年级重庆市凤鸣山中学校联考期末）如图，为正方形边上一点，，，为对角线上一个动点，则的最小值为（ ）
A．5B．C．D．10
【变式训练】
1．（2023秋·吉林长春·八年级长春外国语学校校考期末）如图，在矩形中，，，点在上，点在上，且，连接、，则的最小值为（ ）
A．22B．24C．25D．26
2．（2021春·江苏南京·八年级校考期中）如图，在矩形中，，，点在边上，且，为边上的一个动点，连接，以为边作等边，且点在矩形内，连接，则的最小值为（ ）
A．3B．2C．1D．
3．（2021春·四川凉山·八年级校考期中）如图所示，四边形是正方形，边长为6，点分别在轴、轴的正半轴上，点D在OA上，且点的坐标为，是上一动点，则的最小值为（ ）
A．B．2C．D．
4．（2022秋·江西新余·九年级新余四中校考阶段练习）如图，矩形中，，，，分别是直线，上的两个动点，，沿翻折形成，连接，，则的最小值为（ ）
A．B．C．D．
5．（2022秋·吉林长春·八年级校考期末）如图，中，，，．点D为边上一个动点，作、，垂足为E、F，连接．则长度的最小值为______．
6．（2022秋·山东潍坊·八年级校考期末）如图，在菱形中，点是的中点，，，点为上一动点，求的最小值______．
7．（2022秋·重庆大渡口·九年级校考期末）如图，在矩形中，，，点在边上，点在边上，且，连接，则的最小值为______．
8．（2021秋·陕西渭南·九年级统考期中）如图，在矩形中，，，为上一点，且，为边上的一个动点（不与A重合，可与重合），连接，若以为边向右侧作等腰直角，，连接，则的最小值为________．
9．（2022秋·陕西汉中·九年级校考期中）如图，在正方形中，，为边上一点，．为对角线上一动点（不与点、重合），过点分别作于点、于点，连接、，则的最小值为______．
10．（2022春·江西赣州·八年级统考期末）如图所示，在菱形ABCD中，AB=6，∠BAD=120°，点E，F分别在菱形的边BC，CD上滑动，满足∠EAF=60°，连接EF，且E，F不与B，C，D重合．
(1)求证：不论E，F在BC，CD上如何滑动，总有BE=CF；
(2)当点E，F在BC，CD上滑动时，分别探讨四边形AECF的面积和△CEF的周长是否发生变化？如果不变，求出这个定值；如果变化，求出最小值．
11．（2022秋·河南平顶山·九年级统考期中）如图，在正方形中，点E在对角线上，点F在射线上，且四边形是正方形，连接．
(1)求证：．
(2)______．
(3)著，当点E在上移动时，是否有最小值？若有最小值，求出最小值．
12．（2022秋·广东佛山·八年级校考期中）如图，长方形纸片中，，，折叠纸片的一边，使点D落在边上的点F处，为折痕．请回答下列问题：
(1)______；
(2)试求线段的长度；
(3)若点P为线段上的一个动点，连接和，求线段的最小值．
【考点三 最大值问题】
例题：（2022秋·湖北武汉·九年级统考期中）如图，将两张完全一样的长为，宽为的矩形纸条交叉，使重叠部分的四边形周长最大，则这个最大值是（ ）
A．B．C．D．
【变式训练】
1．（2022·山东菏泽·校考二模）如图，在矩形中，，，连接，是的中点，是上一点，且，是上一动点，则的最大值为（ ）
A．B．C．D．
2．（2022秋·福建漳州·九年级校考期中）如图，平面内三点A、B、C，，，以为对角线作正方形，连接，则的最大值是（ ）
A．6B．11C．D．
3．（2023秋·江苏苏州·八年级校考阶段练习）如图，在中，，，，是的中点，动直线经过点，，，垂足分别为，，则的最大值为 __．
4．（2022秋·全国·九年级专题练习）如图，在菱形ABCD中，AB＝6，，AC与BD交于点O，点N在AC上且AN＝2，点M在BC上且BM＝BC，P为对角线BD上一点，则PM﹣PN的最大值为____．
5．（2022秋·山东济南·九年级统考期中）如图，在菱形ABCD中，，，点M为边中点，点E为菱形四条边上的一个动点，沿的方向运动，连接，以为边作直角三角形，其中，，在点E运动的过程中，线段长度的最大值为______．
6．（2022秋·湖北黄石·九年级校考阶段练习）如图所示，在菱形ABCD中，AB＝6，∠BAD＝120°，△AEF为等边三角形，点E、F分别在菱形的边BC．CD上滑动，且E、F不与B、C、D重合．
（1）计算： =________；
（2）当点E、F在BC、CD上滑动时，△CEF的面积最大值是____________．
7．（2021秋·浙江宁波·八年级校考期中）如图，在长方形纸片ABCD中，AB=3，AD=9，折叠纸片ABCD，使顶点C落在边AD的点G处，折痕分别交边AD、BC于点E、F．
(1)求证：△GEF是等腰三角形
(2)求△GEF面积的最大值．