初中1.2 全等三角形单元测试同步练习题

这是一份初中1.2 全等三角形单元测试同步练习题，文件包含专题111第1章全等三角形单元测试能力过关卷-讲练课堂2022-2023学年八年级数学上册尖子生同步培优题典原卷版苏科版docx、专题111第1章全等三角形单元测试能力过关卷-讲练课堂2022-2023学年八年级数学上册尖子生同步培优题典解析版苏科版docx等2份试卷配套教学资源，其中试卷共28页， 欢迎下载使用。
姓名：__________________ 班级：______________ 得分：_________________
注意事项：
本试卷满分100分，试题共24题．答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置．
一、选择题（本大题共10小题，每小题3分，共30分）在每小题所给出的四个选项中，只有一项是符合题目要求的．
1．（2021秋•泗阳县期末）若△ABC≌△DEF，且∠A＝50°，∠B＝60°，则∠F的度数为（ ）
A．50°B．60°C．70°D．80°
【分析】根据全等三角形的性质得出∠D＝∠A＝50°，∠E＝∠B＝60°，再根据三角形内角和定理求出∠F即可．
【解析】∵△ABC≌△DEF，∠A＝50°，∠B＝60°，
∴∠D＝∠A＝50°，∠E＝∠B＝60°，
∴∠F＝180°﹣∠D﹣∠E＝180°﹣50°﹣60°＝70°，
故选：C．
2．（2021秋•邗江区期末）如图，△ABC≌△ADE，∠DAC＝90°，∠BAE＝140°，BC、DE交于点F，则∠DAB＝（ ）
A．25°B．20°C．15°D．30°
【分析】根据全等三角形的性质得到∠BAC＝∠DAE，进而证明∠BAD＝∠CAE，结合图形计算即可．
【解析】∵△ABC≌△ADE，
∴∠BAC＝∠DAE，
∴∠BAC﹣∠DAC＝∠DAE﹣∠DAC，即∠BAD＝∠CAE，
∵∠DAC＝90°，∠BAE＝140°，
∴∠BAD+∠CAE＝50°，
∴∠BAD＝∠CAE＝25°，
故选：A．
3．（2021秋•连云港期末）如图，已知∠1＝∠2，∠3＝∠4，要证BC＝CD，证明中判定两个三角形全等的依据是（ ）
A．角角角B．角边角C．边角边D．角角边
【分析】已知两角对应相等，且有一公共边，利用全等三角形的判定定理进行推理即可．
【解析】在△ABC与△ADC中，
，
则△ABC≌△ADC（ASA）．
∴BC＝CD．
故选：B．
4．（2021秋•苏州期末）如图，已知AD＝AB，∠C＝∠E，∠CDE＝55°，则∠ABE的度数为（ ）
A．155°B．125°C．135°D．145°
【分析】利用AAS证明△ACD≌△AEB即可得出答案．
【解析】在△ACD和△AEB中，
，
∴△ACD≌△AEB（AAS），
∴∠ABE＝∠ADC，
∵∠CDE＝55°，
∴∠ADC＝180°﹣∠CDE＝180°﹣55°＝125°，
∴∠ABE＝∠ADC＝125°，
故选：B．
5．（2021秋•邳州市期中）如图，一块三角形的玻璃碎成3块（图中所标1、2、3），小华带第3块碎片去玻璃店，购买形状相同、大小相等的新玻璃，这是利用三角形全等中的（ ）
A．SSSB．ASAC．AASD．SAS
【分析】根据题意应先假定选择哪块，再对应三角形全等判定的条件进行验证．
【解析】1、2块玻璃不同时具备包括一完整边在内的三个证明全等的要素，所以不能带它们去，
只有第3块有完整的两角及夹边，符合ASA，满足题目要求的条件，是符合题意的．
故选：B．
6．（2021秋•淮安区期末）如图，已知方格纸中是4个相同的正方形，则∠1+∠2＝（ ）
A．60°B．90°C．100°D．120°
【分析】直接利用全等图形的性质得出∠1＝∠FDE，进而得出答案．
【解析】如图所示：
由题意可得：△ACB≌△DFE，
则∠1＝∠FDE，
∵∠2+∠FDE＝90°，
∴∠1+∠2＝90°．
故选：B．
7．（2020秋•崇川区期末）如图，点D，E分别为△ABC的边AB，AC上的点，连接DE并延长至F，使EF＝DE，连接FC．若FC∥AB，AB＝5，CF＝3，则BD的长等于（ ）
A．1B．2C．3D．5
【分析】由FC∥AB得，∠DAE＝∠FCE，再利用AAS证明△DAE≌△FCE，得AD＝CF，从而解决问题．
【解析】∵FC∥AB，
∴∠DAE＝∠FCE，
在△DAE与△FCE中，
，
∴△DAE≌△FCE（AAS），
∴AD＝CF，
∵CF＝3，
∴AD＝CF＝3，
又∵AB＝5，
∴BD＝AB﹣AD＝5﹣3＝2，
故选：B．
8．（2021春•罗湖区校级期末）如图，D为△ABC边BC上一点，AB＝AC，∠BAC＝56°，且BF＝DC，EC＝BD，则∠EDF等于（ ）
A．62°B．56°C．34°D．124°
【分析】利用SAS得到△FBD≌△DEC得出∠BFD＝∠EDC，求出∠FDB+∠EDC＝∠FDB+∠BFD＝180°﹣∠B＝180°﹣62°＝118°，即可得出答案．
【解析】∵AB＝AC，
∴∠B＝∠C＝（180°﹣∠BAC）＝（180°﹣56°）＝62°，
在△BFD和△EDC中，，
∴△BFD≌△EDC（SAS），
∴∠BFD＝∠EDC，
∴∠FDB+∠EDC＝∠FDB+∠BFD＝180°﹣∠B＝180°﹣62°＝118°，
则∠EDF＝180°﹣（∠FDB+∠EDC）＝180°﹣118°＝62°．
故选：A．
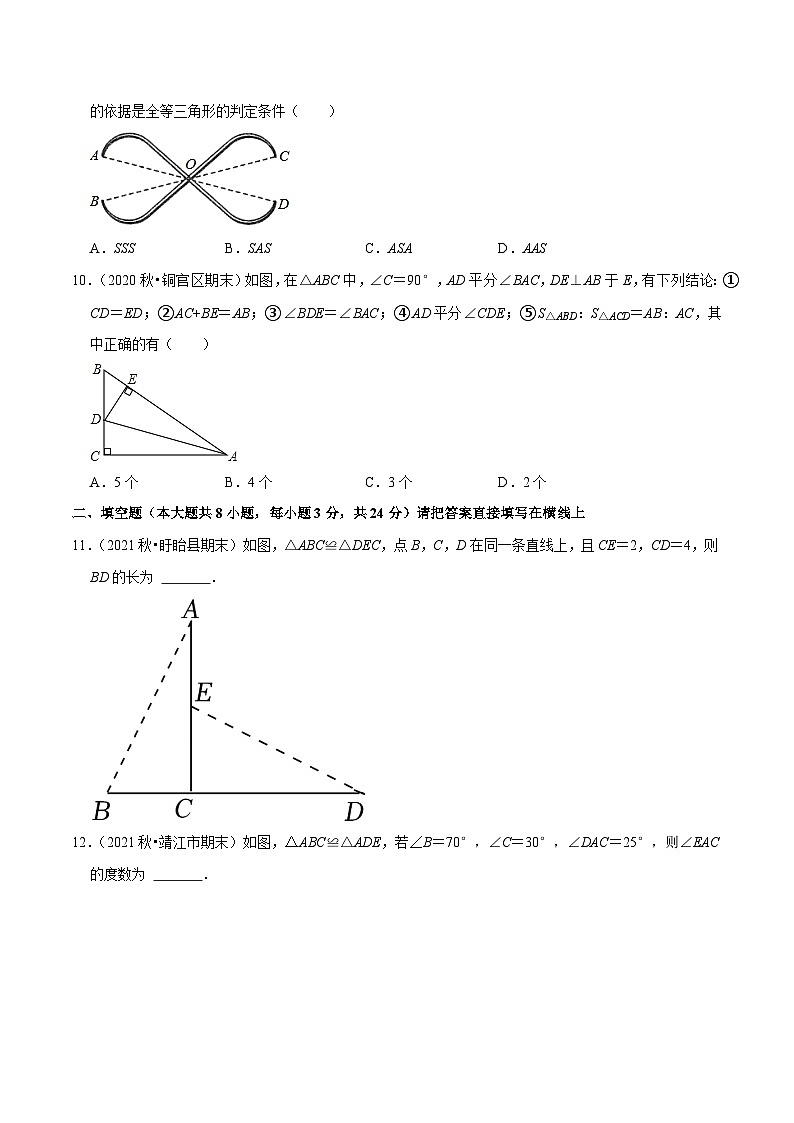
9．（2020秋•茌平区期末）要测量圆形工件的外径，工人师傅设计了如图所示的卡钳，点O为卡钳两柄交点，且有OA＝OB＝OC＝OD，如果圆形工件恰好通过卡钳AB，则此工件的外径必是CD之长了，其中的依据是全等三角形的判定条件（ ）
A．SSSB．SASC．ASAD．AAS
【分析】连接AB、CD，然后利用“边角边”证明△ABO和△DCO全等，根据全等三角形对应边相等解答．
【解析】如图，连接AB、CD，
在△ABO和△DCO中，，
∴△ABO≌△DCO（SAS），
∴AB＝CD．
故选：B．
10．（2020秋•铜官区期末）如图，在△ABC中，∠C＝90°，AD平分∠BAC，DE⊥AB于E，有下列结论：①CD＝ED；②AC+BE＝AB；③∠BDE＝∠BAC；④AD平分∠CDE；⑤S△ABD：S△ACD＝AB：AC，其中正确的有（ ）
A．5个B．4个C．3个D．2个
【分析】根据已知及全等三角形的判定方法进行分析，从而得到答案．
【解析】①正确，因为角平分线上的点到两边的距离相等知；
②正确，因为由HL可知△ADC≌△ADE，所以AC＝AE，即AC+BE＝AB；
③正确，因为∠BDE和∠BAC都与∠B互余，根据同角的补角相等，所以∠BDE＝∠BAC；
④正确，因为由△ADC≌△ADE可知，∠ADC＝∠ADE，所以AD平分∠CDE；
⑤正确，因为CD＝ED，△ABD和△ACD的高相等，所以S△ABD：S△ACD＝AB：AC．
所以正确的有五个，故选：A．
二．填空题（共8小题）
11．（2021秋•盱眙县期末）如图，△ABC≌△DEC，点B，C，D在同一条直线上，且CE＝2，CD＝4，则BD的长为 6 ．
【分析】根据全等三角形的性质得出对应边相等，进而解答即可．
【解析】∵△ABC≌△DEC，CE＝2，CD＝4，
∴BC＝CE＝2，
∴BD＝BC+CD＝4+2＝6，
故答案为：6．
12．（2021秋•靖江市期末）如图，△ABC≌△ADE，若∠B＝70°，∠C＝30°，∠DAC＝25°，则∠EAC的度数为 55° ．
【分析】根据三角形的内角和定理列式求出∠BAC，再根据全等三角形对应角相等可得∠DAE＝∠BAC，然后根据∠EAC＝∠DAE﹣∠DAC代入数据进行计算即可得解．
【解析】∵∠B＝70°，∠C＝30°，
∴∠BAC＝180°﹣70°﹣30°＝80°，
∵△ABC≌△ADE，
∴∠DAE＝∠BAC＝80°，
∴∠EAC＝∠DAE﹣∠DAC＝80°﹣25°＝55°．
故答案为：55°．
13．（2021秋•阜宁县期末）在Rt△ABC中，∠ACB＝90°，BC＝4cm，CD⊥AB，在AC上取一点E，使EC＝4cm，过点E作EF⊥AC交CD的延长线于点F．若AE＝1cm，则EF＝ 5 cm．
【分析】由CD⊥AB，EF⊥AC就可以得出∠FEC＝∠ADC＝90°，就有∠A＝∠F，就可以得出△ABC≌△FCE，就有EF＝AC而求出结论．
【解析】∵CD⊥AB，EF⊥AC，
∴∠FEC＝∠ADC＝∠ACB＝90°，
∴∠ACD+∠A＝∠ACD+∠F＝90°，
∴∠A＝∠F，
∵BC＝EC＝4cm，
在△ABC和△FCE中，
，
∴△ABC≌△FCE（AAS），
∴AC＝FE，
∵AC＝AE+EC，
∴FE＝AE+EC，
∵EC＝4cm，AE＝1cm，
∴FE＝4+1＝5cm．
故答案为：5．
14．（2022•建湖县一模）如图，AE∥DF，AE＝DF．添加下列条件中的一个：①AB＝CD；②EC＝BF；③∠E＝∠F；④EC∥BF．其中能证明△ACE≌△DBF的是 ①③④ ．（只填序号）
【分析】根据平行线的性质求出∠A＝∠D，∠ECA＝∠FBD，根据AB＝DC求出AC＝DB，再根据全等三角形的判定定理逐个判断即可．
【解析】∵AE∥DF，
∴∠A＝∠D，
①∵AB＝CD，
∴AB+BC＝DC+BC，
即AC＝DB，
AE＝DF，∠A＝∠D，AC＝DB，符合全等三角形的判定定理SAS，能推出△ACE≌△DBF，故①正确；
②根据AE＝DF，∠A＝∠D和EC＝BF不能推出△ACE≌△DBF，故②错误；
③∠A＝∠D，AE＝DF，∠E＝∠F，符合全等三角形的判定定理ASA，能推出△ACE≌△DBF，故③正确；
④∵EC∥BF，
∴∠ECA＝∠FBD，
∠ECA＝∠FBD，∠A＝∠D，AE＝DF，符合全等三角形的判定定理AAS，能推出△ACE≌△DBF，故④正确；
即正确的有①③④，
故答案为：①③④．
15．（2021秋•勃利县期末）如图所示，AB＝AC，AD＝AE，∠BAC＝∠DAE，∠1＝25°，∠2＝30°，则∠3＝ 55° ．
【分析】求出∠BAD＝∠EAC，证△BAD≌△CAE，推出∠2＝∠ABD＝30°，根据三角形的外角性质求出即可．
【解析】∵∠BAC＝∠DAE，
∴∠BAC﹣∠DAC＝∠DAE﹣∠DAC，
∴∠1＝∠EAC，
在△BAD和△CAE中，
∴△BAD≌△CAE（SAS），
∴∠2＝∠ABD＝30°，
∵∠1＝25°，
∴∠3＝∠1+∠ABD＝25°+30°＝55°，
故答案为：55°．
16．（2020秋•常熟市期中）如图，△ABC中，∠A＝90°，AB＝8，BD∥AC，且BD＝BC，过点D作DE⊥BC，垂足为E．若CE＝2，则BD的长为 17 ．
【分析】根据AAS证明△ABC≌△EDB，由全等三角形的性质得出AB＝DE＝8，根据勾股定理可得出答案．
【解析】∵DE⊥BC，
∴∠DEB＝90°，
∵AC∥BD，
∴∠A＝∠ABD＝∠DEB＝90°，
∵∠ABC+∠CBD＝90°，
∴∠CBD+∠BDE＝90°，
∴∠ABC＝∠BDE，
在△ABC和△EDB中，
，
∴△ABC≌△EDB（AAS），
∴AB＝DE＝8，
设BD＝x，则BE＝x﹣2，
∵BE2+DE2＝BD2，
∴（x﹣2）2+82＝x2，
∴x＝17，
∴BD＝17．
故答案为：17．
17．（2020秋•南京期中）我们把顶点在小正方形顶点上的三角形叫做格点三角形，在如图所示的方格纸中，除了格点三角形ABC外，可画出与△ABC全等的格点三角形共有 15 个．
【分析】用SSS判定两三角形全等．认真观察图形可得答案．
【解析】用SSS判定两三角形全等，所以共有16个全等三角形，
除去△ABC外有15个与△ABC全等的三角形．
故答案为：15．
18．（2020春•雨花区期末）如图，在四边形ABCD中，AB＝AD，∠BAD＝140°，AB⊥CB于点B，AD⊥CD于点D，E、F分别是CB、CD上的点，且∠EAF＝70°，下列说法正确的是 ③⑤ ．（填写正确的序号）
①DF＝BE，②△ADF≌△ABE，③FA平分∠DFE，④AE平分∠FAB，⑤BE+DF＝EF，⑥CF+CE＞FD+EB．
【分析】延长EB到G，使BG＝DF，连接AG，根据全等三角形的判定定理求出△ADF≌△ABG，根据全等三角形的性质得出AF＝AG，∠G＝∠DFA，∠DAF＝∠BAG，求出∠FAE＝∠EAG＝70°，根据全等三角形的判定定理得出△FAE≌△GAE，根据全等三角形的性质得出∠FEA＝∠GEA，∠G＝∠EFA，EF＝EG，再进行判断即可．
【解析】延长EB到G，使BG＝DF，连接AG，
∵AB⊥CB，AD⊥CD，
∴∠D＝∠ABG＝90°，
在△ADF和△ABG中
，
∴△ADF≌△ABG（SAS），
∴AF＝AG，∠G＝∠DFA，∠DAF＝∠BAG，
∵∠EAF＝70°，∠DAB＝140°，
∴∠DAF+∠EAB＝∠DAB﹣∠FAE＝140°﹣70°＝70°，
∴∠EAG＝∠EAB+∠BAG＝∠EAB+∠FAD＝70°，
∴∠FAE＝∠EAG＝70°，
在△FAE和△GAE中
，
∴△FAE≌△GAE（SAS），
∴∠FEA＝∠GEA，∠G＝∠EFA，EF＝EG，
∴EF＝EB+DF，∠FAE≠∠EAB，故⑤正确，④错误；
∴∠G＝∠EFA＝∠DFA，即AF平分∠DFE，故③正确；
∵CF+CE＞EF，EF＝DF+BE，
∴CF+CE＞DF+BE，
当D和F重合时，EF＜DF+BE，即不能推出CF+CE＞DF+BE，故⑥错误；
根据已知不能推出△ADF≌△ABE，故①错误，②错误；
故答案为：③⑤．
三．解答题（共6小题）
19．（2022•丰县二模）如图，点F是△ABC的边AC的中点，点D在AB上，连接DF并延长至点E，DF＝EF，连接CE．
（1）求证：△ADF≌△CEF；
（2）若DE∥BC，DE＝4，求BC的长．
【分析】（1）根据线段中点求出AF＝CF，再根据全等三角形的判定定理SAS推出即可；
（2）根据全等三角形的性质得出∠A＝∠ACE，根据平行线的判定得出AB∥CE，根据平行四边形的判定定理得出四边形BCED是平行四边形，再根据平行四边形的性质得出即可．
【解答】（1）证明：∵F为AC的中点，
∴AF＝CF，
在△ADF和△CEF中，
，
∴△ADF≌△CEF（SAS）；
（2）解：∵△ADF≌△CEF，
∴∠A＝∠ACE，
∴AB∥CE，
∵DE∥BC，
∴四边形BCED是平行四边形，
∴BC＝DE，
∵DE＝4，
∴BC＝4．
20．（2022•工业园区模拟）已知：如图，AB＝AC，AD＝AE，∠BAE＝∠CAD．求证：∠D＝∠E．
【分析】先证∠BAD＝∠CAE，再证△BAD≌△CAE（SAS），即可得出结论．
【解答】证明：∵∠BAE＝∠CAD，
∴∠BAE+∠DAE＝∠CAD+∠DAE，
即∠BAD＝∠CAE，
在△BAD与△CAE中，
，
∴△BAD≌△CAE（SAS），
∴∠D＝∠E．
21．（2020春•宽城区期末）如图，△ACF≌△DBE，其中点A、B、C、D在一条直线上
（1）若BE⊥AD，∠F＝62°，求∠A的大小；
（2）若AD＝9cm，BC＝5cm，求AB的长．
【分析】（1）根据全等三角形的性质得到∠FCA＝∠EBD＝90°，根据直角三角形的性质计算即可；
（2）根据全等三角形的性质得到CA＝BD，结合图形得到AB＝CD，计算即可．
【解析】（1）∵BE⊥AD，
∴∠EBD＝90°，
∵△ACF≌△DBE，
∴∠FCA＝∠EBD＝90°，
∴∠A＝90°﹣∠F＝28°；
（2）∵△ACF≌△DBE，
∴CA＝BD，
∴CA﹣CB＝BD﹣BC，即AB＝CD，
∵AD＝9cm，BC＝5cm，
∴AB+CD＝9﹣5＝4cm，
∴AB＝2cm．
22．（2021•梁溪区一模）如图，△ABC≌△DEF，AM、DN分别是△ABC和△DEF的中线．求证：AM＝DN．
【分析】根据全等三角形的性质得出AB＝DE，∠E＝∠B，利用AAS证明△ABM与△DEN全等，进而证明即可．
【解答】证明：∵△ABC≌△DEF，
∴AB＝DE，∠B＝∠E，
∵AM、DN分别是△ABC和△DEF的中线，
∴BM＝BC，EN＝EF．
∴BM＝EN．
在△ABM和△DEN中，
，
∴△ABM≌△DEN（SAS），
∴AM＝DN．
23．（2020春•南岗区校级期中）已知：点A、F、E、C在同一条直线上，AF＝CE，BE∥DF，BE＝DF．
（1）如图1，求证：△ABE≌△CDF．
（2）如图2，连接AD、BC、BF、DE，在不添加任何辅助线的情况下，请直接写出图2中所有全等的三角形（除△ABE全等于△CDF外）．
【分析】（1）先求出AE＝CF，根据平行线的性质得出∠AEB＝∠CFD，再根据全等三角形的判定定理SAS推出即可；
（2）根据全等三角形的判定定理得出全等三角形即可．
【解答】（1）证明：∵AF＝CE，
∴AF+EF＝CE+EF，
即AE＝CF，
∵BE∥DF，
∴∠AEB＝∠CFD，
在△ABE和△CDF中
，
∴△ABE≌△CDF（SAS）；
（2）图2中的全等三角形有△ABC≌△CDA，△AFB≌△CED，△ADE≌△CBF，△ADF≌△CBE，△BFE≌△DEF，
理由是：∵△ABE≌△CDF，
∴AB＝CD，∠BAC＝∠DCA，
在△ABC和△CDA中
，
∴△ABC≌△CDA（SAS），
∴AD＝BC，∠DAC＝∠BCA，
在△AFB和△CED中
，
∴△AFB≌△CED（SAS），
∴BF＝DE，
在△ADE和△CBF中
，
∴△ADE≌△CBF（SAS），
在△ADF和△CBE中
，
∴△ADF≌△CBE（SAS），
∴DF＝BE，
在△BEF和△DFE中
，
∴△BEF≌△DFE（SSS）．
24．（2020春•南岸区期末）在∠MAN内有一点D，过点D分别作DB⊥AM，DC⊥AN，垂足分别为B，C．且BD＝CD，点E，F分别在边AM和AN上．
（1）如图1，若∠BED＝∠CFD，请说明DE＝DF；
（2）如图2，若∠BDC＝120°，∠EDF＝60°，猜想EF，BE，CF具有的数量关系，并说明你的结论成立的理由．
【分析】（1）根据题目中的条件和∠BED＝∠CFD，可以证明△BDE≌△CDF，从而可以得到DE＝DF；
（2）作辅助线，过点D作∠CDG＝∠BDE，交AN于点G，从而可以得到△BDE≌△CDG，然后即可得到DE＝DG，BE＝CG，再根据题目中的条件可以得到△EDF≌△GDF，即可得到EF＝GF，然后即可得到EF，BE，CF具有的数量关系．
【解析】（1）∵DB⊥AM，DC⊥AN，
∴∠DBE＝∠DCF＝90°，
在△BDE和△CDF中，
∵
∴△BDE≌△CDF（AAS）．
∴DE＝DF；
（2）EF＝FC+BE，
理由：过点D作∠CDG＝∠BDE，交AN于点G，
在△BDE和△CDG中，
，
∴△BDE≌△CDG（ASA），
∴DE＝DG，BE＝CG．
∵∠BDC＝120°，∠EDF＝60°，
∴∠BDE+∠CDF＝60°．
∴∠FDG＝∠CDG+∠CDF＝60°，
∴∠EDF＝∠GDF．
在△EDF和△GDF中，
，
∴△EDF≌△GDF（SAS）．
∴EF＝GF，
∴EF＝FC+CG＝FC+BE．