专题2.10等腰三角形的性质与判定大题专练（重难点培优）-【讲练课堂】2022-2023学年八年级数学上册尖子生同步培优题典【苏科版】

这是一份专题2.10等腰三角形的性质与判定大题专练（重难点培优）-【讲练课堂】2022-2023学年八年级数学上册尖子生同步培优题典【苏科版】，文件包含专题210等腰三角形的性质与判定大题专练重难点培优-讲练课堂2022-2023学年八年级数学上册尖子生同步培优题典原卷版苏科版docx、专题210等腰三角形的性质与判定大题专练重难点培优-讲练课堂2022-2023学年八年级数学上册尖子生同步培优题典解析版苏科版docx等2份试卷配套教学资源，其中试卷共44页， 欢迎下载使用。

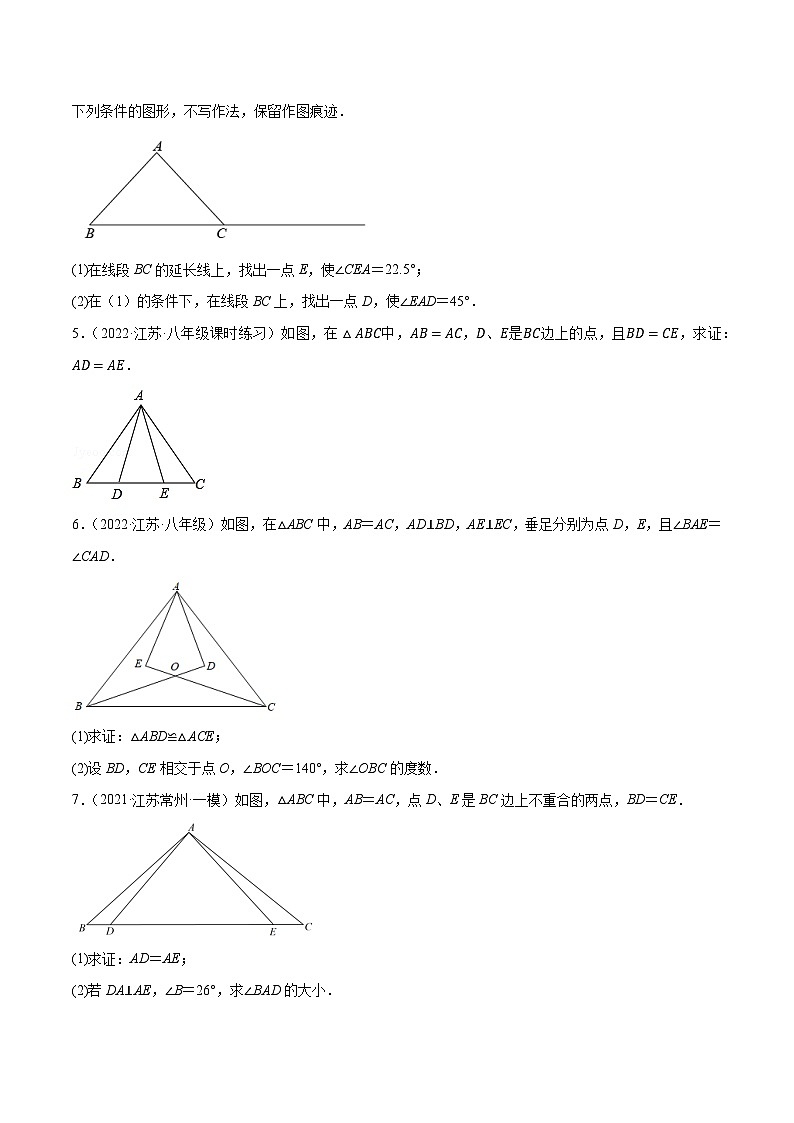
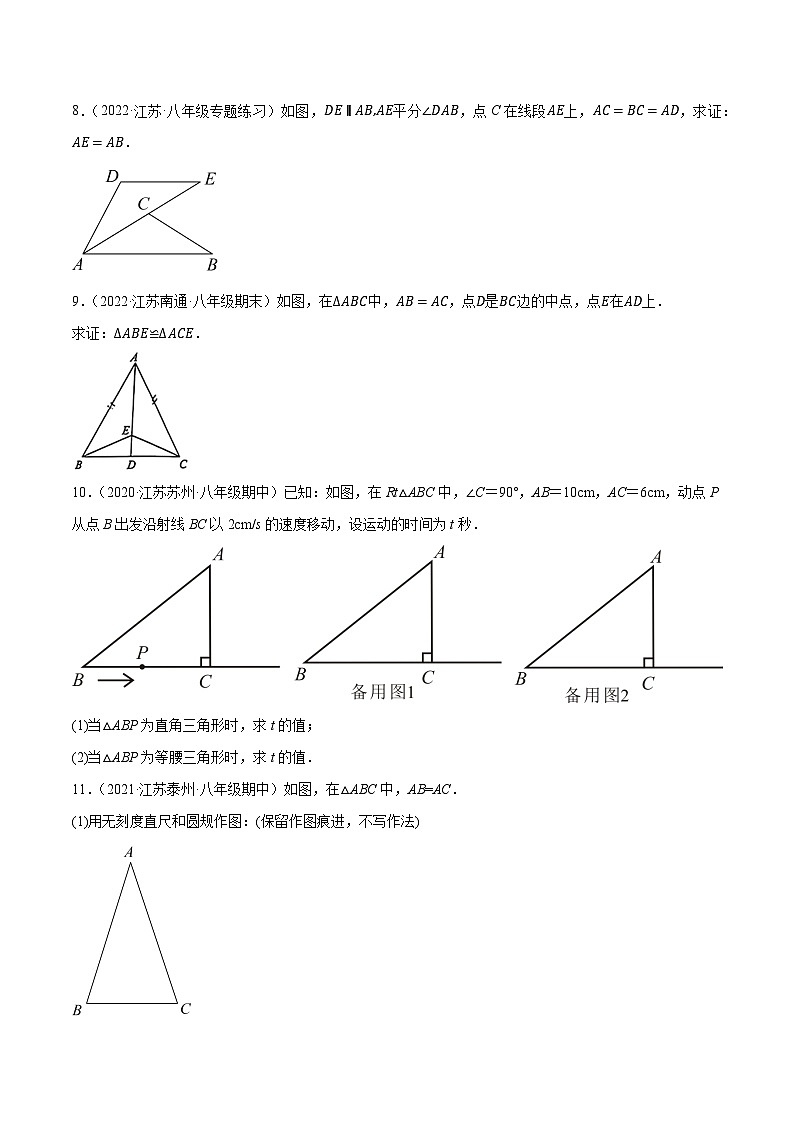
【讲练课堂】2022-2023学年八年级数学上册尖子生同步培优题典【苏科版】专题2.10等腰三角形的性质与判定大题专练（重难点培优）一、解答题（共24题）1．（2022·江苏·八年级专题练习）如图，在四边形ABCD中，AD∥BC，点E为对角线BD上一点，∠A＝∠BEC，且AD＝BE．(1)求证：ΔABD≅ΔECB；(2)若∠BDC＝70°，求∠DBC的度数．2．（2022·江苏·八年级专题练习）如图，AD⊥BC，AD＝BD，∠C=70°，求∠BAC的度数．3．（2022·江苏·九年级专题练习）如图，点E是△ABC的边BC上一点，∠DAB=∠DEB=∠CAE，AD=AB，AB、DE相交于点F．(1)求证：△ADE≌△ABC；(2)若∠C=70∘．①当AE=BE时，求∠DAE的度数；②当△ABC的外心在其内部时，直接写出∠B的取值范围．4．（2022·江苏泰州·一模）如图，在△ABC中，∠BAC＝90°，AB＝AC．请用无刻度的直尺和圆规作出符合下列条件的图形，不写作法，保留作图痕迹．(1)在线段BC的延长线上，找出一点E，使∠CEA＝22.5°；(2)在（1）的条件下，在线段BC上，找出一点D，使∠EAD＝45°．5．（2022·江苏·八年级课时练习）如图，在△ABC中，AB=AC，D、E是BC边上的点，且BD=CE，求证：AD=AE．6．（2022·江苏·八年级）如图，在△ABC中，AB＝AC，AD⊥BD，AE⊥EC，垂足分别为点D，E，且∠BAE＝∠CAD．(1)求证：△ABD≌△ACE；(2)设BD，CE相交于点O，∠BOC＝140°，求∠OBC的度数．7．（2021·江苏常州·一模）如图，△ABC中，AB＝AC，点D、E是BC边上不重合的两点，BD＝CE．(1)求证：AD＝AE；(2)若DA⊥AE，∠B＝26°，求∠BAD的大小．8．（2022·江苏·八年级专题练习）如图，DE∥AB,AE平分∠DAB，点C在线段AE上，AC=BC=AD，求证：AE=AB．9．（2022·江苏南通·八年级期末）如图，在ΔABC中，AB=AC，点D是BC边的中点，点E在AD上．求证：ΔABE≌ΔACE．10．（2020·江苏苏州·八年级期中）已知：如图，在Rt△ABC中，∠C＝90°，AB＝10cm，AC＝6cm，动点P从点B出发沿射线BC以2cm/s的速度移动，设运动的时间为t秒．(1)当△ABP为直角三角形时，求t的值；(2)当△ABP为等腰三角形时，求t的值．11．（2021·江苏泰州·八年级期中）如图，在△ABC中，AB=AC．(1)用无刻度直尺和圆规作图：(保留作图痕进，不写作法)①作∠BAC的平分线交BC于点D．②作边AC的中点E，连接DE．(2)在(1)所作的图中，若AD=12，BC=10，求DE的长．12．（2021·江苏·常州实验初中八年级阶段练习）如图，在ΔABC中，AB=AC，D是BC边上的中点，DE⊥AB于点E，DF⊥AC于点F．求证：DE=DF．13．（2022·江苏·八年级专题练习）如图，点A，C，D，B四点共线，且AC=BD，∠A=∠B，∠ADE=∠BCF．（1）求证：△ADE≌△BCF；（2）若DE=9，CG=4，求线段EG的长．14．（2020·江苏·无锡市钱桥中学八年级阶段练习）如图，在△ABC中，AD⊥BC，垂足为D，AD=4，BD=2，CD=8．（1）求证：∠BAC=90°；（2）P为BC边上一点，连接AP，若△ABP为等腰三角形，请直接写出BP的长．15．（2021·江苏苏州·二模）如图，在ΔABC中，BD⊥AC于点D,P为BD上的点，∠PAC=45°,AB=CP．（1）求证：CD=BD;（2）若∠CPA=105°,AB=2,求PB的长．16．（2019·江苏无锡·八年级期中）如图，在Rt△ABC中，∠ACB＝90°，BC＝30cm，AC＝40cm，点D在线段AB上，从点B出发，以2cm/s的速度向终点A运动，设点D的运动时间为t秒．（1）点D在运动t秒后，BD＝ cm（用含有t的式子表示）（2）AB＝    cm ，AB 边上的高为    cm ；（3）点D在运动过程中，当△BCD为等腰三角形时，求t的值．17．（2022·江苏·八年级）如图△ABC是等边三角形，BD是中线，延长BC到E，使CE＝CD．求证：DB＝DE．18．（2022·江苏·南京玄武外国语学校八年级期末）如图，在RtΔABC和RtΔEFD中，∠ABC=90°，∠EFD=90°，AC=ED，AC⊥ED，垂足为M．连接EA，连接EC并延长交AB的延长线于点G．（1）求证△ABC≌△EFD；（2）若∠G=45°，求证EA=ED．19．（2022·江苏盐城·八年级开学考试）如图，点C在线段AB上，AD∥EB，AC＝BE，AD＝BC．CF平分∠DCE．求证：（1）△ACD≌△BEC；       （2）CF⊥DE．20．（2021·江苏泰州·八年级期末）如图1，在△ABC中，∠ABC、∠ACB的平分线相交于点O，过点O作MN∥BC．分别交AB、AC于M、N．（1）求证：BM+CN＝MN．（2）如图2，若△ABC是等边三角形，请从以下两个问题任选一题作答．若两题都作答，以问题①计分．问题①BC＝6，求MN的长．问题②求证：O是MN的中点．21．（2021·江苏苏州·一模）已知：在RtΔABC中，∠BAC=90°，AB=AC，点D为BC边中点.点M为线段BC上的一个动点（不与点C，点D重合），连接AM，将线段AM绕点M顺时针旋转90°，得到线段ME，连接EC．（1）如图1，若点M在线段BD上，求∠MCE的度数；（2）如图2，若点M在线段CD上，试探究线段AC、CE、CM之间的数量关系，并证明你的结论．22．（2021·江苏泰州·一模）已知：如图1，△ACD中，AD≠CD．（1）请你以AC为一边，在AC的同侧构造一个与△ACD全等的三角形△ACE，画出图形；（要求：尺规作图，保留作图痕迹，不写作法）（2）参考（1）中构造全等三角形的方法解决下面问题：如图2，在四边形ABCD中①∠ACB+∠CAD=180°；②∠B=∠D；③CD=AB．请在上述三条信息中选择其中两条作为条件，其余的一条信息作为结论组成一个命题．试判断这个命题是否正确，并说明理由你选择的条件是________，结论是_______（只要填写序号）23．（2022·江苏淮安·七年级期末）学完《全等三角形》一章后，我们知道“斜边和一条直角边分别相等的两个直角三角形全等（简称“HL”定理）”是判定直角三角形全等的特有方法．(1)如图1，在△ABC和△DCB中，∠A=∠D=90°，AC=DB，AC和DB交于点E，则线段AE和线段DE的数量关系是_________；(2)如图2，在△ABC中，∠BAC=90°，AB=AC，点D、E分别在边AC、AB上，且CE=BD．求证：AE=AD；(3)如图3，在△ABC中，∠BAC为钝角，AB=AC，点D、E分别在边AC、AB上，且CE=BD，则线段AE与线段AD相等吗？如果相等，请给出证明；如果不相等，请说明理由．24．（2021·江苏南京·一模）若两条线段将一个三角形分割成三个等腰三角形，则这两条线段称为三分线．（1）如图①，△ABC中，AB＝AC，∠A＝36°，请在图中画出两条三分线，并标出每个等腰三角形顶角的度数（画出一种分割即可）．（2）如图②，△ABC中，∠C＝90°，∠A＝60°，请在图中画出两条三分线，并标出每个等腰三角形顶角的度数（画出一种分割即可）．（3）如图③，△ABC中，∠BAC为钝角，AE，DE为三分线，BD＝BE，DA＝DE，CA＝CE．①求∠B和∠C的关系式．②求∠BAC的取值范围．