江苏省南京市金陵中学河西分校2023-2024学年七年级下学期期中考试数学试题

这是一份江苏省南京市金陵中学河西分校2023-2024学年七年级下学期期中考试数学试题，共19页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1．（2分）下列生活现象中，属于平移的是（ ）
A．卫星绕地球运动B．钟表指针的运动
C．电梯从底楼升到顶楼D．教室门从开到关
2．（2分）下列计算正确的是（ ）
A．a2•a3＝a6B．a8÷a2＝a6C．（a2）4＝a6D．3a5﹣2a5＝1
3．（2分）若一个多边形的每一个外角都是36°，则这个多边形的边数是（ ）
A．7B．8C．9D．10
4．（2分）若（y2+ay+2）（2y﹣4）的结果中不含y2项，则a的值为（ ）
A．0B．2C．D．﹣2
5．（2分）如图，是可调躺椅示意图，AE与BD的交点为C，∠B，∠E保持不变．为了舒适，使∠EFD＝110°．根据图中数据信息，下列调整∠D大小的方法正确的是（ ）
A．增大10°B．减小10°C．增大15°D．减小15°
6．（2分）在△ABC中，点D，E分别在AB，且CD与BE相交于点F，已知△BDF的面积为10，△CEF的面积为16，则四边形区域ADFE的面积等于（ ）
A．22B．24C．36D．44
二、填空题：（本题共10小题，每小题2分，共20分）.
7．（2分）每个生物携带自身基因的载体是生物细胞的DNA，DNA分子的直径只有0.0000002cm，将0.0000002用科学记数法表示为 ．
8．（2分）若（2a﹣1）0＝1成立，a的取值范围是 ．
9．（2分）等腰三角形两边长分别是3和6，则该三角形的周长为 ．
10．（2分）若x2+2（m﹣3）x+16是关于x的完全平方式，则m＝ ．
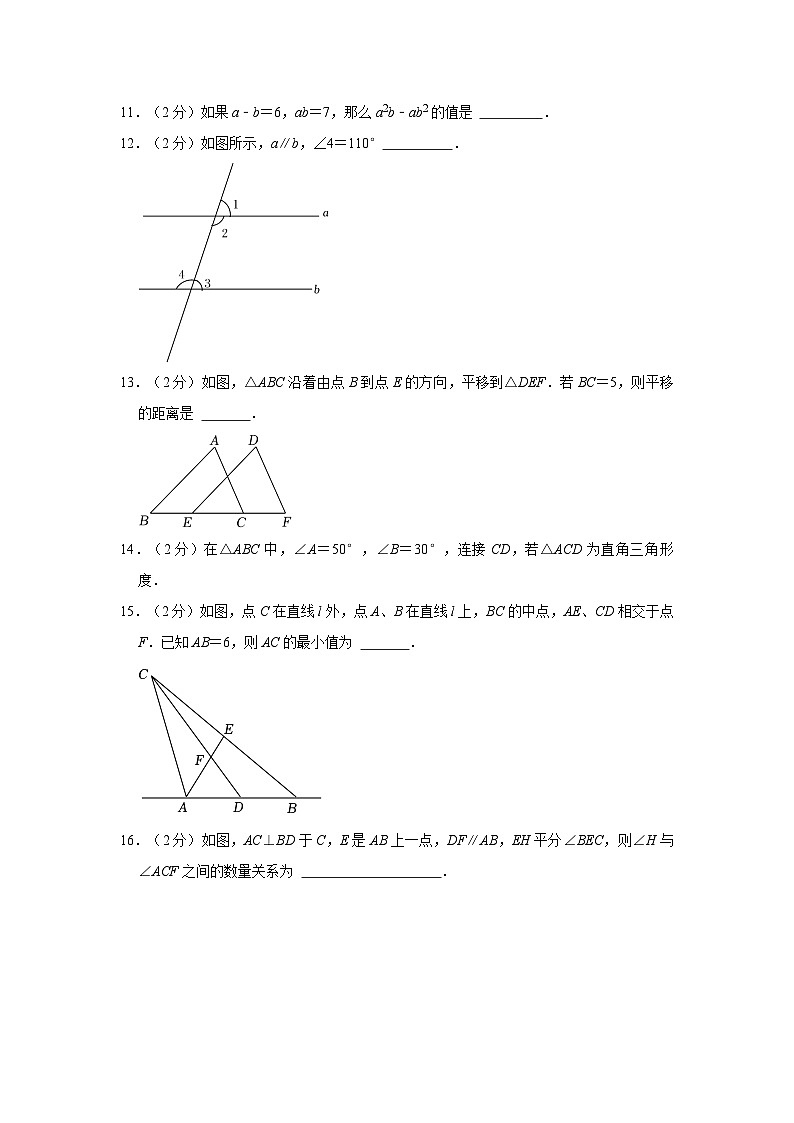
11．（2分）如果a﹣b＝6，ab＝7，那么a2b﹣ab2的值是 ．
12．（2分）如图所示，a∥b，∠4＝110° ．
13．（2分）如图，△ABC沿着由点B到点E的方向，平移到△DEF．若BC＝5，则平移的距离是 ．
14．（2分）在△ABC中，∠A＝50°，∠B＝30°，连接CD，若△ACD为直角三角形 度．
15．（2分）如图，点C在直线l外，点A、B在直线l上，BC的中点，AE、CD相交于点F．已知AB＝6，则AC的最小值为 ．
16．（2分）如图，AC⊥BD于C，E是AB上一点，DF∥AB，EH平分∠BEC，则∠H与∠ACF之间的数量关系为 ．
三、解答题：（本题共10小题，共68分．解答应写出文字说明，证明过程或演算步骤）．
17．（6分）计算：
（1）；
（2）a3•a5﹣（2a4）2+a10÷a2．
18．（6分）分解因式：
（1）4a2﹣9；
（2）x3﹣4x2y+4xy2．
19．（5分）先化简，再求值：（a+b）（a﹣b）﹣（a﹣b）2+2b2，其中a＝﹣3，b＝．
20．（6分）按图填空，并注明理由．已知：如图，DE∥BC
证明：∵DE∥BC（已知），
∴∠B＝ （ ）．
∵∠DEF＝∠B（已知）
∴∠DEF＝ ．
∴ ∥EF（ ），
∴∠A＝∠CEF（ ）．
21．（6分）已知：如图，∠ABE+∠CEB＝180°，∠1＝∠2
22．（8分）如图，每个小正方形的边长为1个单位，每个小方格的顶点叫格点．
（1）画出△ABC先向右平移6格再向下平移2格所得的△A'B'C'；
（2）画出△ABC的中线BD；
（3）△ABC的面积为 ；
（4）连接AA'，BB'，则AA'与BB'的关系是 ．
23．（6分）“直角三角形的两个锐角互余”的逆命题是 ，请证明这个逆命题是真命题．
已知： ；
求证： ．
24．（8分）规定两数a，b之间的一种运算，记作（a，b）c＝b，那么（a，b）＝c．例如：因为23＝8，所以（2，8）＝3．
（1）根据上述规定，填空：（3，9）＝ ，（ ，16）＝2，（﹣2，﹣8）＝ ；
（2）有同学在研究这种运算时发现一个现象：（3n，4n）＝（3，4），他给出了如下的证明：
设 （3n，4n）＝x，
∴（3n）x＝4n
即（3，4）＝x，
∴（3n，4n）＝（3，4）．
①若（4，5）＝a，（4，6）＝b，（4，30），请你尝试运用上述这种方法证明a+b＝c；
②猜想[（x﹣1）n，（y+1）n]+[（x﹣1）n，（y﹣2）n]＝（ ， ）（结果化成最简形式）．
25．（8分）如图，已知长方形ABCD中，AD＝10cm，点F是DC的中点，点E从A点出发在AD上以每秒1cm的速度向D点运动（假定0＜t＜10）
（1）当t＝5秒时，求阴影部分（即三角形BEF）的面积；
（2）用含t的式子表示阴影部分的面积；
（3）过点E作EG∥AB交BF于点G，过点F作FH∥BC交BE于点H，请直接写出在E点运动过程中
26．（9分）如图，在△ABC中，点D在AB上，交AC于点E，DP平分∠ADE，CP与DE相交于点G，∠ACF的平分线CQ与DP相交于点Q．
（1）若∠A＝50°，∠B＝60°，则∠DPC＝ °，∠Q °；
（2）若∠A＝50°，当∠B的度数发生变化时，∠DPC、∠Q的度数是否发生变化？并说明理由；
（3）若△PCQ中存在一个内角等于另一个内角的三倍，请直接写出所有符合条件的∠A的度数 ．
参考答案与试题解析
一、选择题：（本题共6小题，每小题2分，共12分）.
1．（2分）下列生活现象中，属于平移的是（ ）
A．卫星绕地球运动B．钟表指针的运动
C．电梯从底楼升到顶楼D．教室门从开到关
【解答】解：A、卫星绕地球运动，故A不符合题意；
B、钟表指针的运动，故B不符合题意；
C、电梯从底楼升到顶楼，故C符合题意；
D、教室门从开到关，故D不符合题意；
故选：C．
2．（2分）下列计算正确的是（ ）
A．a2•a3＝a6B．a8÷a2＝a6C．（a2）4＝a6D．3a5﹣2a5＝1
【解答】解：A．a2⋅a3＝a8，故本选项错误，不符合题意；
B．a8÷a2＝a7，故本选项正确，符合题意；
C．（a2）4＝a5，故本选项错误，不符合题意；
D．3a5﹣2a5＝a5，故本选项错误，不符合题意；
故选：B．
3．（2分）若一个多边形的每一个外角都是36°，则这个多边形的边数是（ ）
A．7B．8C．9D．10
【解答】解：∵一个多边形的每一个外角都是36°，
∴这个多边形的边数为，
故选：D．
4．（2分）若（y2+ay+2）（2y﹣4）的结果中不含y2项，则a的值为（ ）
A．0B．2C．D．﹣2
【解答】解：（y2+ay+2）（3y﹣4）
＝2y8﹣4y2+4ay2﹣8ay+4y﹣8
＝2y6+（﹣4+2a）y6+（﹣8a+4）y﹣7，
∵结果中不含y2项，
∴﹣4+8a＝0，
解得：a＝2．
故选：B．
5．（2分）如图，是可调躺椅示意图，AE与BD的交点为C，∠B，∠E保持不变．为了舒适，使∠EFD＝110°．根据图中数据信息，下列调整∠D大小的方法正确的是（ ）
A．增大10°B．减小10°C．增大15°D．减小15°
【解答】解：延长EF，交CD于点G
∵∠ACB＝180°﹣50°﹣60°＝70°，
∴∠ECD＝∠ACB＝70°．
∵∠DGF＝∠DCE+∠E，
∴∠DGF＝70°+30°＝100°．
∵∠EFD＝110°，∠EFD＝∠DGF+∠D，
∴∠D＝10°．
而图中∠D＝20°，
∴∠D应减少10°．
故选：B．
6．（2分）在△ABC中，点D，E分别在AB，且CD与BE相交于点F，已知△BDF的面积为10，△CEF的面积为16，则四边形区域ADFE的面积等于（ ）
A．22B．24C．36D．44
【解答】解：如图，连AF△ADF＝m，
∵S△BDF：S△BCF＝10：20＝1：2＝DF：CF，
则有4m＝S△AEF+S△EFC，
S△AEF＝2m﹣16，
而S△BFC：S△EFC＝20：16＝5：6＝BF：EF，
又∵S△ABF：S△AEF＝BF：EF＝5：4，
而S△ABF＝m+S△BDF＝m+10，
∴S△ABF：S△AEF＝BF：EF＝3：4＝（m+10）：（2m﹣16），
解得m＝20．
S△AEF＝5×20﹣16＝24，
SADEF＝S△AEF+S△ADF＝24+20＝44．
故选：D．
二、填空题：（本题共10小题，每小题2分，共20分）.
7．（2分）每个生物携带自身基因的载体是生物细胞的DNA，DNA分子的直径只有0.0000002cm，将0.0000002用科学记数法表示为 2×10﹣7 ．
【解答】解：0.0000002＝2×10﹣4，
故答案为：2×10﹣7．
8．（2分）若（2a﹣1）0＝1成立，a的取值范围是 a≠ ．
【解答】解：∵（2a﹣1）2＝1成立，
∴2a﹣2≠0，
∴a≠，
故答案为：a≠．
9．（2分）等腰三角形两边长分别是3和6，则该三角形的周长为 15 ．
【解答】解：由三角形的三边关系可知，由于等腰三角形两边长分别是3和6，
所以其另一边只能是4，
故其周长为6+6+6＝15．
故答案为15．
10．（2分）若x2+2（m﹣3）x+16是关于x的完全平方式，则m＝ ﹣1或7 ．
【解答】解：∵x2+2（m﹣7）x+16是关于x的完全平方式，
∴2（m﹣3）＝±4，
解得：m＝﹣1或7，
故答案为：﹣6或7．
11．（2分）如果a﹣b＝6，ab＝7，那么a2b﹣ab2的值是 42 ．
【解答】解：a2b﹣ab2
＝ab（a﹣b），
当a﹣b＝8，ab＝7时，
原式＝7×7＝42，
故答案为：42．
12．（2分）如图所示，a∥b，∠4＝110° 70° ．
【解答】解：∵a∥b，
∴∠4＝∠2，
∵∠5+∠1＝180°，
∴∠4+∠5＝180°，
∵∠4＝110°，
∴∠1＝70°，
故答案为：70°．
13．（2分）如图，△ABC沿着由点B到点E的方向，平移到△DEF．若BC＝5，则平移的距离是 2 ．
【解答】解：由题意平移的距离为BE＝BC﹣EC＝5﹣3＝8，
故答案为：2．
14．（2分）在△ABC中，∠A＝50°，∠B＝30°，连接CD，若△ACD为直角三角形 60或10 度．
【解答】解：分两种情况：
①如图1，当∠ADC＝90°时，
∵∠B＝30°，
∴∠BCD＝90°﹣30°＝60°；
②如图2，当∠ACD＝90°时，
∵∠A＝50°，∠B＝30°，
∴∠ACB＝180°﹣30°﹣50°＝100°，
∴∠BCD＝100°﹣90°＝10°，
综上，则∠BCD的度数为60°或10°；
故答案为：60或10；
15．（2分）如图，点C在直线l外，点A、B在直线l上，BC的中点，AE、CD相交于点F．已知AB＝6，则AC的最小值为 6 ．
【解答】解：如图，连接BF，
∵点D、E分别是AB，
∴＝S△ADC＝S△BDC，S△AFD+S△BFD，S△CEF＝S△BEF，
∴S△CEF+S四边形BDFE＝S△CEF+SACF，S△AFD+S△CEF＝S△BEF+S△BFD＝S四边形BDFE＝7，
∴S四边形BDFE＝S△ACF＝6，
∴S△ABC＝S△ACF+S四边形BDFE+S△AFD+S△CEF＝18，
∴＝18，
∴CH＝6，
∵点到到直线的距离垂线段最短，
∴AC≥CH＝6，
∴AC的最小值为4．
故答案为：6．
16．（2分）如图，AC⊥BD于C，E是AB上一点，DF∥AB，EH平分∠BEC，则∠H与∠ACF之间的数量关系为 2∠H+∠ACF＝180° ．
【解答】解：延长EC，交DH于K，
∵∠EKD＝∠HEC+∠H，∠ECD＝∠EKD+∠HDC，
∴∠ECD＝∠HEC+∠HDC+∠H，
∵DF∥AB，
∴∠B＝∠BDG，
∵EH平分∠BEC，DH平分∠BDG，
∴∠HEC＝∠BEC∠B，
∵∠BEC＝∠A+∠ACE，
∴∠HEC＝∠A+，
∴∠ECD＝∠A+∠B+∠H，
∵AC⊥BD，
∴∠A+∠B＝90°，
∴∠ECD＝45°+∠ACE+∠H，
∵AC⊥BD，
∴∠ECD＝90°+∠ACE，
∴90°+∠ACE＝45°+∠ACE+∠H，
∴90°+∠ACE＝2∠H，
∴90°+（90°﹣∠ACF）＝2∠H，即4∠H+∠ACF＝180°．
故答案为：2∠H+∠ACF＝180°．
三、解答题：（本题共10小题，共68分．解答应写出文字说明，证明过程或演算步骤）．
17．（6分）计算：
（1）；
（2）a3•a5﹣（2a4）2+a10÷a2．
【解答】解：（1）
＝﹣1﹣4+4
＝﹣4；
（2）a3•a3﹣（2a4）6+a10÷a2
＝a8﹣7a8+a8
＝﹣2a8．
18．（6分）分解因式：
（1）4a2﹣9；
（2）x3﹣4x2y+4xy2．
【解答】解：（1）原式＝（2a+3）（3a﹣3）．
（2）原式＝x（x2﹣7xy+4y2）＝x（x﹣7y）2．
19．（5分）先化简，再求值：（a+b）（a﹣b）﹣（a﹣b）2+2b2，其中a＝﹣3，b＝．
【解答】解：原式＝a2﹣b2﹣a3+2ab﹣b2+4b2＝2ab，
当a＝﹣7，b＝时．
20．（6分）按图填空，并注明理由．已知：如图，DE∥BC
证明：∵DE∥BC（已知），
∴∠B＝ ∠ADE （ 两直线平行，同位角相等 ）．
∵∠DEF＝∠B（已知）
∴∠DEF＝ ∠ADE ．
∴ AB ∥EF（ 内错角相等，两直线平行 ），
∴∠A＝∠CEF（ 两直线平行，同位角相等 ）．
【解答】解：∵DE∥BC（已知），
∴∠B＝∠ADE（两直线平行，同位角相等），
∵∠DEF＝∠B（已知），
∴∠DEF＝∠ADE，
∴AB∥EF（内错角相等，两直线平行），
∴∠A＝∠CEF（两直线平行，同位角相等），
故答案为：∠ADE；两直线平行；∠ADE；内错角相等；两直线平行．
21．（6分）已知：如图，∠ABE+∠CEB＝180°，∠1＝∠2
【解答】证明：∵∠ABE+∠CEB＝180°，
∴AB∥CD，
∴∠ABE＝∠DEB，
即：∠1+∠MBE＝∠2+∠NEB，
又∵∠6＝∠2，
∴∠MBE＝∠NEB，
∴BM∥EN，
∴∠M＝∠N．
22．（8分）如图，每个小正方形的边长为1个单位，每个小方格的顶点叫格点．
（1）画出△ABC先向右平移6格再向下平移2格所得的△A'B'C'；
（2）画出△ABC的中线BD；
（3）△ABC的面积为 7 ；
（4）连接AA'，BB'，则AA'与BB'的关系是 平行且相等 ．
【解答】解：（1）如图，△A'B'C'即为所求；
（2）如图，BD即为所求；
（3）△ABC的面积＝4×4﹣1×6﹣2×7＝7，
故答案为：7；
（4）AA'与BB'的关系是平行且相等．
故答案为：平行且相等．
23．（6分）“直角三角形的两个锐角互余”的逆命题是 如果三角形有两个角互余，则三角形为直角三角形 ，请证明这个逆命题是真命题．
已知： ∠A+∠B＝90° ；
求证： △ABC是直角三角形 ．
【解答】解：“直角三角形的两个锐角互余”的逆命题为：如果三角形有两个角互余，则三角形为直角三角形．
已知：∠A+∠B＝90°，
求证：△ABC是直角三角形；
故答案为：如果三角形有两个角互余，则三角形为直角三角形；△ABC是直角三角形．
24．（8分）规定两数a，b之间的一种运算，记作（a，b）c＝b，那么（a，b）＝c．例如：因为23＝8，所以（2，8）＝3．
（1）根据上述规定，填空：（3，9）＝ 2 ，（ ±4 ，16）＝2，（﹣2，﹣8）＝ 3 ；
（2）有同学在研究这种运算时发现一个现象：（3n，4n）＝（3，4），他给出了如下的证明：
设 （3n，4n）＝x，
∴（3n）x＝4n
即（3，4）＝x，
∴（3n，4n）＝（3，4）．
①若（4，5）＝a，（4，6）＝b，（4，30），请你尝试运用上述这种方法证明a+b＝c；
②猜想[（x﹣1）n，（y+1）n]+[（x﹣1）n，（y﹣2）n]＝（ （x﹣1） ， （y2﹣y﹣2） ）（结果化成最简形式）．
【解答】解：（1）∵32＝6，
∴（3，9）＝2；
∵（±4）2＝16，
∴（±3，16）＝2；
∵（﹣2）7＝﹣8，
∴（﹣2，﹣6）＝3．
故答案为：2，±2，3；
（2）①∵（4，5）＝a，6）＝b，30）＝c，
∴4a＝3，4b＝6，3c＝30，
∴4a×4b＝3×6＝30＝4c，
∴3a+b＝4c，
即a+b＝c；
②设[（x﹣1）n，（y+2）n]＝p，[（x﹣1）n，（y﹣2）n]＝q，
由上述结论，知（x﹣3）p＝y+1，（x﹣1）q＝y﹣7，
且[（x﹣1）n，（y+1）n]+[（x﹣2）n，（y﹣2）n]＝p+q，
∵（x﹣1）p×（x﹣5）q＝（y+1）（y﹣2），
即（x﹣8）p+q＝y2﹣y﹣2，
∴[（x﹣2），（y2﹣y﹣2]＝p+q，
∴[（x﹣3）n，（y+1）n]+[（x﹣1）n，（y﹣7）n]＝[（x﹣1），（y2﹣y﹣5]．
故答案为：（x﹣1），（y2﹣y﹣7）．
25．（8分）如图，已知长方形ABCD中，AD＝10cm，点F是DC的中点，点E从A点出发在AD上以每秒1cm的速度向D点运动（假定0＜t＜10）
（1）当t＝5秒时，求阴影部分（即三角形BEF）的面积；
（2）用含t的式子表示阴影部分的面积；
（3）过点E作EG∥AB交BF于点G，过点F作FH∥BC交BE于点H，请直接写出在E点运动过程中
【解答】解：（1）∵长方形ABCD中，AD＝10cm，点F是DC的中点，
∴DF＝CF＝3（cm），
当t＝5秒时，AE＝7×1＝5（cm），
∴DE＝AD﹣AE＝10﹣7＝5（cm），
∴S阴影＝S矩形ABCD﹣S△ABE﹣S△DEF﹣S△BCF
＝10×6﹣×5×5﹣×10×3
＝60﹣15﹣3.5﹣15
＝22.5（cm7）；
（2）由题意得：AE＝t cm，DE＝（10﹣t）cm，
∵S阴影＝S矩形ABCD﹣S△ABE﹣S△DEF﹣S△BCF
＝10×6﹣×6t﹣×10×7
＝（30﹣t）（cm7），
即阴影部分的面积为（30﹣t）cm2；
（3）∵四边形ABCD是长方形，
∴AD⊥CD，AB∥CD，
∵EG∥AB，FH∥BC，
∴EG⊥HF、AD⊥EG，
∴DE、AE分别等于△EGF，DF、△BHF的FH边上的高，
∴S△BEF＝EG•DE+EG（DE+AE）＝，
同理：S△BEF＝FH•DC，
∴EG•AD＝FH•DC，
即10EG＝6FH，
∴＝＝．
26．（9分）如图，在△ABC中，点D在AB上，交AC于点E，DP平分∠ADE，CP与DE相交于点G，∠ACF的平分线CQ与DP相交于点Q．
（1）若∠A＝50°，∠B＝60°，则∠DPC＝ 115 °，∠Q 25 °；
（2）若∠A＝50°，当∠B的度数发生变化时，∠DPC、∠Q的度数是否发生变化？并说明理由；
（3）若△PCQ中存在一个内角等于另一个内角的三倍，请直接写出所有符合条件的∠A的度数 45°或60°或120°或135° ．
【解答】解：（1）∵∠A＝50°，∠B＝60°，
∴∠ACB＝70°，
∴∠BCP＝∠ACB＝35°，
∵DE∥BC，
∴∠ADE＝∠B＝60°，∠PGD＝∠PCB＝35°，
∵∠PDE＝∠ADE＝30°，
∴∠DPC＝180°﹣∠PDE﹣∠PGD＝115°；
又∵∠ACQ＝∠ACF，
∴∠PCQ＝∠ACQ+∠ACP＝（∠ACF+∠ACB）＝90°，
∴∠Q＝∠DPC﹣∠QCP＝25°；
故答案为：115，25；
（2）∠DPC、∠Q的度数不会发生变化．
理由：由（1）得：∵∠PDE＝∠ADE＝，∠PGD＝∠BCP＝，
∴∠DPC＝180°﹣∠PDE﹣∠PGD＝180°﹣∠B﹣（180°﹣∠A）＝90°+；
∴∠Q＝∠DPC﹣∠QCP＝25°；
（3）设∠A＝x，则，
∵CP平分∠ACB，CQ平分∠ACF，
∴，，
∴，，
因为△PCQ中存在一个内角等于另一个内角的三倍，
∴①当∠Q＝7∠QPC时，，
∴x＝135°，
②当∠QPC＝7∠Q时，，
∴x＝45°，
③当∠PCQ＝4∠Q时，，
∴x＝60°，
④当∠PCQ＝3∠QPC时，，
∴x＝120°，
综上①②③④可知∠A＝45°或60°或120°或135°．
故答案为：45°或60°或120°或135°．