重庆市江津区16校联盟学校2023-2024学年九年级下学期期中考试数学试题（原卷版+解析版）

这是一份重庆市江津区16校联盟学校2023-2024学年九年级下学期期中考试数学试题（原卷版+解析版），文件包含重庆市江津区16校联盟学校2023-2024学年九年级下学期期中考试数学试题原卷版docx、重庆市江津区16校联盟学校2023-2024学年九年级下学期期中考试数学试题解析版docx等2份试卷配套教学资源，其中试卷共41页， 欢迎下载使用。

（满150分，考试时间120分钟）
参考公式：抛物线顶点坐标为，对称轴为
一、选择题（本大题共10个小题，每小题4分，共40分）
1. 的绝对值是（ ）
A. 2024B. C. D.
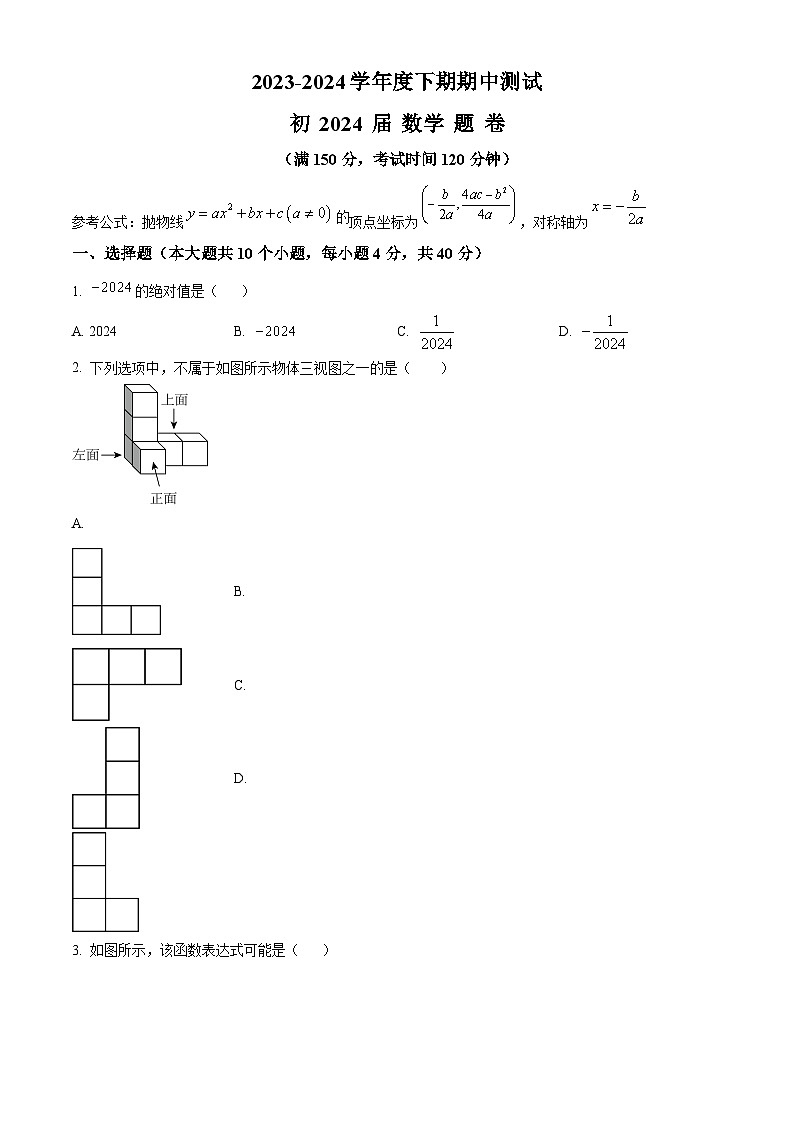
2. 下列选项中，不属于如图所示物体三视图之一的是（ ）
A.
B.
C.
D.

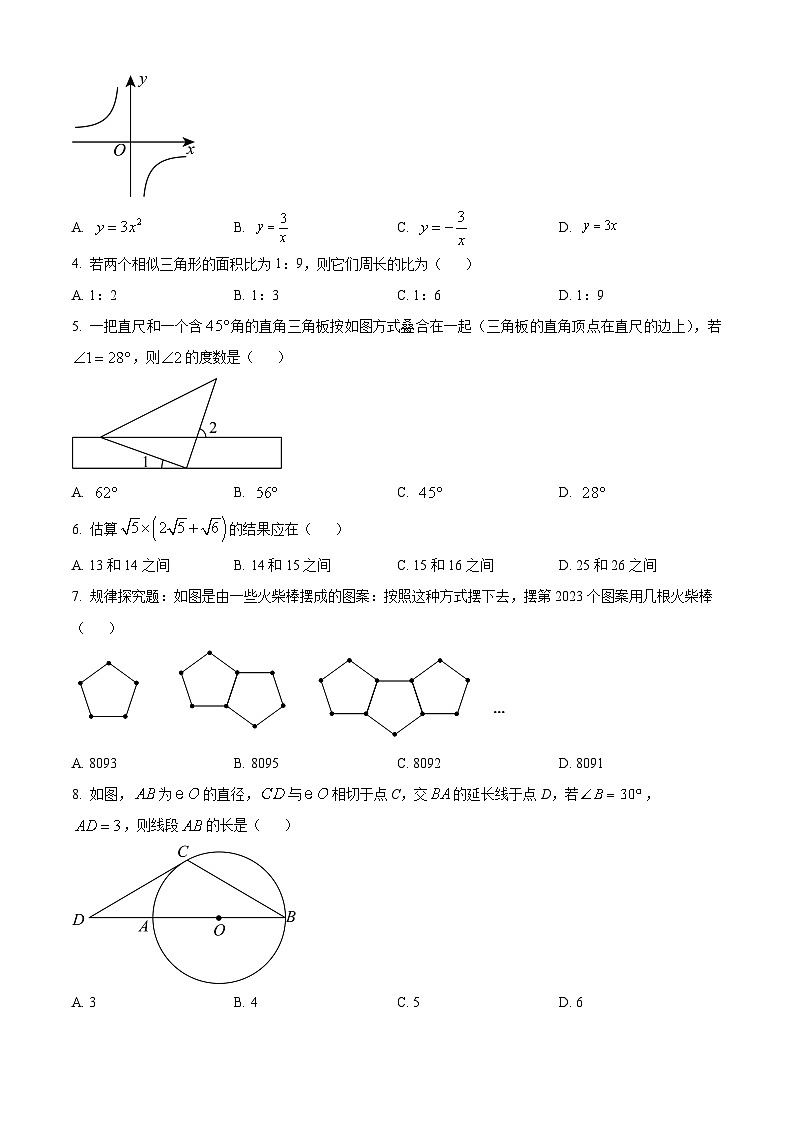
3. 如图所示，该函数表达式可能是（ ）
A. B. C. D.
4. 若两个相似三角形的面积比为1：9，则它们周长的比为（ ）
A. 1：2B. 1：3C. 1：6D. 1：9
5. 一把直尺和一个含角的直角三角板按如图方式叠合在一起（三角板的直角顶点在直尺的边上），若，则的度数是（ ）
A. B. C. D.
6. 估算的结果应在（ ）
A. 13和14之间B. 14和15之间C. 15和16之间D. 25和26之间
7. 规律探究题：如图是由一些火柴棒摆成的图案：按照这种方式摆下去，摆第2023个图案用几根火柴棒（ ）
A. 8093B. 8095C. 8092D. 8091
8. 如图，为的直径，与相切于点C，交的延长线于点D，若，，则线段的长是（ ）
A. 3B. 4C. 5D. 6
9. 如图，在正方形中，点E是上一点，过点E作交于点F，连接，，若，则的度数是（ ）
A. B. C. D.
10. 已知，对多项式任意添加绝对值运算（不可添加为单个字母的绝对值或绝对值中含有绝对值的情况）后仍只含减法运算，称这种操作为“绝对领域”，例如：， 等，下列相关说法正确的个数是（ ）
①一定存在一种“绝对领域”操作使得操作后的式子化简的结果为非负数；②一定存在一种“绝对领域”操作使得操作后的式子化简的结果与原式互为相反数；③进行“绝对领域”操作后的式子化简的结果可能有11种结果．
A 0B. 1C. 2D. 3
二、填空题（本大题共8个小题，每小题4分，共32分）
11. 计算：________.
12. 如图，若的半径为3，则其内接正六边形的周长为______．
13. 在一个不透明的袋中装着4个球，3个红球和1个黄球，这些球除颜色外无其他差别，从袋子中随机摸出2个小球，两球恰好是一个黄球和一个红球的概率为___．
14. 某市实施科技强市的战略，为加强科技基础研究能力，逐步加大了对科研经费的投入，2022年投入科研经费6000万元，2024年投入经费8000万元．设科研经费投入的年平均增长率为，根据题意可列方程为______．
15. 在中，于点D，以为斜边作，与交于点E，使得，连接，，若，则的长为__________．
16. 如图所示，是半圆的直径，将直径绕点顺时针旋转得对应线段，若，则图中阴影部分的面积是______．

17. 如果关于x的不等式组至少有两个整数解，且关于y的分式方程的解为正整数，则符合条件的所有整数m的和为__________．
18. 若一个四位数的千位数字比百位数字大1，十位数字比个位数字大2，则称这个四位数是“惊蛰数”，若其千位数字比百位数字大2，十位数字比个位数字大4，则称这个四位数是“谷雨数”，如3220是“惊蛰数”，6495是“谷雨数”，最小的“谷雨数”是_____________；若、分别是“惊蛰数”、“谷雨数”，且它们的个位数字均为2，、各数位上的数字之和分别记为和，若能被10整除．则当取得最小值时的值是_____________．
三、解答题（本大题共8个小题，第19题8分，其余每题各10分，共78分）
19. 计算：
（1）；
（2）．
20. 在中，是的角平分线，作线段的垂直平分线，分别交、，于点E、O、F，连接、，证明四边形是菱形．
（1）尺规作图：作线段的垂直平分线，分别交、，于点E、O、F，连接、（用基本作图，保留作图痕迹，不写作法、结论）
（2）证明：四边形是菱形．
证明：平分，
____________________
是线段的垂直平分线，
，
，
在与中，
，
，
__________________
四边形是菱形．（____________________）
21. 语文王老师为了了解同学们的语文寒假作业完成情况，进行了一个简单的练习，现从1班，2班中各随机抽取名学生的练习成绩（满分分，分及分以上为合格）进行整理、描述和分析，下面给出了部分信息：
1班名学生的练习成绩为：，，，，，，，，，，，，，，，，，，，．
2班名学生的练习成绩条形统计图如图：
1班、2班抽取的学生的练习成绩的平均数、众数、中位数、分及以上人数所占百分比如表所示：
（1）直接写出上述表中的，，的值；
（2）根据以上数据，你认为班，班中哪个班学生掌握知识较好？请说明理由（写出一条理由即可）；
（3）1班，班共名学生参加此次练习，估计参加此次练习成绩合格的学生人数是多少？
22. 重庆动物园“四喜丸子”火爆全网，为迎接即将到来“五一”旅游热，重庆一玩具加工厂计划甲车间加工熊猫玩偶840个．工作6天后还未加工完，于是增加了工人人数，增加工人后每天加工玩偶的个数比增加前多加工20个，又加工了两天才完成了任务．
（1）求甲车间增加工人人数后每天加工熊猫玩偶的个数；
（2）由于该玩偶深受消费者喜欢，工厂决定扩大生产，安排乙车间加工生产该熊猫玩偶2000个，该车间在加工完成一半后，改进了加工技术，每天比改进技术前多加工，结果比原计划提前5天完成任务，求乙车间改进技术前每天加工玩偶的个数．
23 如图，在矩形中，，，动点，分别以每秒1个单位长度的速度同时从点和点出发，点沿折线方向运动，点沿折线方向运动，当点到达点时停止运动．设运动时间为秒，的面积为．
（1）请直接写出关于的函数表达式并注明自变量的取值范围；
（2）在给定的平面直角坐标系中画出这个函数的图象，并写出该函数的一条性质；
（3）结合函数图象，写出当的面积不小于6且不大于11时的取值范围．
24. 如图，四边形是一湿地公园的休闲步道.经测量，于点B，米，点D在C的北偏东方向，且点D在A的东北方向．
（1）求步道的长度；（精确到个位数）
（2）小庆以80米/分的速度沿B→C→D→A的方向步行，小渝骑自行车以200米/分的速度沿B→A→D→C的方向行驶．两人同时出发能否在9分钟内相遇？请说明理由．（参考数据：，，）
25. 如图，在平面直角坐标系xOy中，已知抛物线交轴于点，，与y轴交于点C．
（1）求抛物线的函数表达式；
（2）如图1，若点M是第四象限内抛物线上一点，轴交于点N，求的最大值；
（3）如图2，在轴上取一点，抛物线沿方向平移个单位得新抛物线，新抛物线与轴交于点，，交轴于点，点在线段上运动，线段关于线段对称线段所在直线交新抛物线于点，直线与直线所成夹角为，直接写出点的横坐标．
26. 在中，，点为延长线上任一点，连接．
（1）如图，若，，求线段的长；
（2）如图，将线段绕着点逆时针旋转得到线段，连接．点为的中点，连接．求证：；
（3）在（）的条件下，设点为直线上的点，交于点．点在延长线上运动的过程中，当时，将沿直线翻折到所在平面内得到，同时将沿直线翻折到所在平面内得到．在取得最大值时，请直接写出的值．
年级
平均数
众数
中位数
分及以上人数所占百分比
1班
2班