




初中数学苏科版八年级下册9.2 中心对称与中心对称图形多媒体教学ppt课件
展开中心对称中心对称的性质中心对称的作图中心对称图形
1. 定义:一个图形绕着某一点旋转 180°,如果它能够与另一个图形重合,那么称这两个图形关于这点对称,也称这两个图形成中心对称,这个点叫做对称中心.这两个图形在旋转后能重合的对应点叫做关于对称中心的对称点.
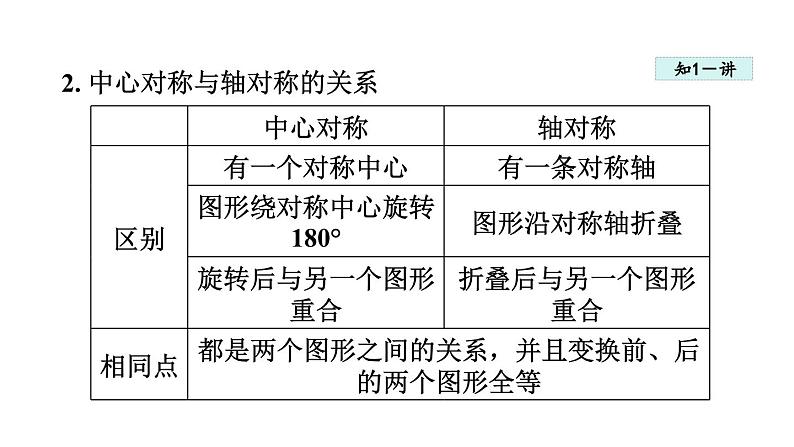
2. 中心对称与轴对称的关系
特别解读1. 中心对称是特殊的旋转,其旋转角为180° .2. 中心对称是指两个图形的位置关系,必须涉及两个图形.3. 中心对称的两个图形,只有一个对称中心 . 这个对称中心可能在图形的外部,也可能在图形的内部或边上 .
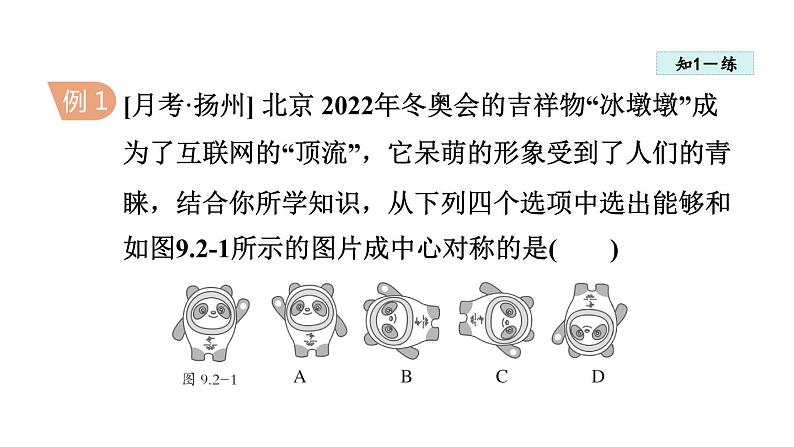
[月考·扬州] 北京 2022年冬奥会的吉祥物“冰墩墩”成为了互联网的“顶流”,它呆萌的形象受到了人们的青睐,结合你所学知识,从下列四个选项中选出能够和如图9.2-1所示的图片成中心对称的是( )
解题秘方:紧扣中心对称的定义求解.
解:由题意可知,选项A是原图形翻折得到的,是轴对称变换,选项B是原图形逆时针方向旋转 90°得到的,选项 C是原图形顺时针方向旋转 90°得到的,选项 D是原图形旋转 180°得到的,故D选项符合题意.
解法提醒中心对称是对两个图形而言,它表示两个图形之间的对称关系;中心对称是一种特殊的旋转,旋转角为180°,注意与平移、轴对称的区别 .
1. 性质(1)成中心对称的两个图形中,对应点的连线都经过对称中心,且被对称中心平分;反之,如果两个图形的对应点的连线都经过某一点,并且被这一点平分,那么这两个图形关于这一点成中心对称,利用这一性质可以识别中心对称;(2)中心对称的两个图形是全等图形,对应角相等,对应线段平行(或在同一直线上)且相等 .
2. 确定对称中心的方法方法一:连接任意一对对称点,取这条线段的中点,则该中点为对称中心;方法二:连接任意两对对称点,这两条线段的交点就是对称中心 .
特别解读1. 由性质可以得到如下结论:(1)对称中心在一对对称点的连线上 ;(2)对称中心到一对对称点的距离相等 .2. 全等的图形不一定成 中心对称,而成中心对称的两个图形一定是全等的图形 .
如图 9.2-2,已知四边形ABCD与四边形A1B1C1D1成中心对称,请回答下列问题:(1)点A的对称点是点______,点B的对称点是______点 ,对称中心是点_______;
解题秘方:紧扣中心对称的性质进行判断 .
(2)指出图中在同一条直线上的三点;(3)指出图中相等的线段和全等的三角形 .
解:A,O,A1;B,O,B1;C,O,C1;D,O,D1.
图中相等的线段有 OA=OA1,OB=OB1,OC=OC1,OD=OD1,AB=A1B1,BC=B1C1,CD=C1D1,DA=D1A1;全等的三角形有△ABO与△A1B1O,△ADO与△ A1D1O,△BCO与△B1C1O,△DCO与△D1C1O.
解法提醒找对称点是解决问题的关键,每一对对称点与对称中心在同一条直线上,根据对称点来找对应线段、对应角,由中心对称的性质得到对应线段、对应角的相等关系,从而确定三角形的形状和大小关系 .
1. 作图关键 确定对称中心,再作出原图形上关键点关于对称中心的对称点 .2. 作图步骤(1)连接:分别将原图形上的所有关键点与对称中心连接;
(2)延长:将以上连线延长找对称点,使得对称点与对称中心的距离和关键点与对称中心的距离相等;(3)连接:将对称点按原图形的形状顺次连接起来,即可得出关于对称中心对称的图形 .
特别提醒作一个图形关于某点成中心对称的图形,要运用中心对称的性质,将已知图形的关键点与对称中心连接并延长至某点,使之到对称中心的距离与已知关键点到对称中心的距离相等 .
如图 9.2-3,已知四边形ABCD和点O,画四边形A′B′C′D′,使四边形A′B′C′D′与四边形ABCD关于点O成中心对称.
解题秘方:要作四边形ABCD关于点O成中心对称的图形,只要作出点A,B,C,D关于点O的对称点,然后顺次连接即可 .
解:(1)连接AO并延长AO到 A′,使OA′=OA,于是得到点A关于点O的对称点A′;(2)同样画出点B,C和D关于点O的对称点B′,C′ 和D′;(3)连接A′B′,B′C′,C′D′,D′A′,则四边形A′B′C′D′即为所求作的图形.如图 9.2-4所示.
作图通法作已知图形关于某一点对称的图形:1. 作图依据:对称中心是对称点所连线段的中点 .2. 作图步骤(概括为):(1)连接;(2)延长;(3)等长截取;(4)顺次连接对称点 .
1. 中心对称图形把一个图形绕着某一点旋转 180°,如果旋转后的图形能够与原来的图形互相重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心 .
2. 中心对称图形的性质(1)中心对称图形上对称点的连线必经过对称中心,且被对称中心平分,即过对称中心的直线与中心对称图形所交的两点是对称点. 中心对称图形上所有的点关于对称中心的对称点都在这个图形上;(2)过对称中心的任一直线把中心对称图形分成全等的两部分.
3. 中心对称与中心对称图形的区别和联系
特别提醒判断中心对称图形的方法:1. 中心对称图形的“三要素”:(1)对称中心;(2)旋转180°;(3)与本身重合.2. 常见的中心对称图形:线段、平行四边形、矩形、菱形、边数是偶数的正多边形、圆等.
[中考·宿迁] 对称美是美的一种重要形式,它能给予人们一种圆满、均匀、协调和平衡的美感,下列图形属于中心对称图形的是( )
解题秘方:紧扣中心对称图形的定义做出判断.
解:选项A 中的图形绕正方形对角线的交点旋转180 度后与自身重合,故选项A 中的图形是中心对称图形;选项B,C,D 中的图形沿某条直线对折后两边能完全重合,而绕圆心旋转180 度后不能与自身重合,故选项B,C,D 中的图形是轴对称图形而不是中心对称图形.
方法点拨判断一个图形是不是轴对称图形,就看是否存在一条直线(对称轴),使得这个图形沿这条直线对折后两边能完全重合;判断一个图形是不是中心对称图形,可以把纸倒过来看(相当于旋转180°),如果看到的图形与原来的图形完全相同,就是中心对称图形,否则就不是.
苏科版八年级下册9.2 中心对称与中心对称图形教课ppt课件: 这是一份苏科版八年级下册9.2 中心对称与中心对称图形教课ppt课件,共21页。PPT课件主要包含了情境创设,轴对称,做一做,知识理解,课本62页第1题等内容,欢迎下载使用。
2021学年第9章 中心对称图形——平行四边形9.2 中心对称与中心对称图形评课ppt课件: 这是一份2021学年第9章 中心对称图形——平行四边形9.2 中心对称与中心对称图形评课ppt课件,共36页。PPT课件主要包含了自主先学,情境创设,轴对称,合作助学,做一做,确定对称中心的方法,课本62页第1题等内容,欢迎下载使用。
苏科版八年级下册第9章 中心对称图形——平行四边形9.2 中心对称与中心对称图形试讲课ppt课件: 这是一份苏科版八年级下册第9章 中心对称图形——平行四边形9.2 中心对称与中心对称图形试讲课ppt课件,共17页。PPT课件主要包含了情境创设,探索活动一,数学化认识,练一练,探索活动二,轴对称,中心对称,轴对称图形,中心对称图形,沿对称轴翻折等内容,欢迎下载使用。













