2024年河北省文化课中考一模数学试题（原卷版+解析版）

这是一份2024年河北省文化课中考一模数学试题（原卷版+解析版），文件包含2024年河北省文化课中考一模数学试题原卷版docx、2024年河北省文化课中考一模数学试题解析版docx等2份试卷配套教学资源，其中试卷共34页， 欢迎下载使用。

（试卷页数：8页，考试时间：120分钟，总分：120分）
一、选择题（本大题共16个小题，共38分.1~6小题各3分；7~16小题各2分，在每小题给出的四个选项中，只有一项是符合题目要求的）
1. 如图，过上一点作的切线，可以作（ ）
A. 0条B. 1条C. 2条D. 无数条
【答案】B
【解析】
【分析】本题考查了切线．熟练掌握切线定义是解题的关键．
根据切线的定义进行判断作答即可．
【详解】解：过上一点作的切线，可以作1条，
故选：B．
2. 若非零实数x满足，则的值为（ ）
A. 1B. 3C. D.
【答案】D
【解析】
【分析】本题考查了一元一次方程的解，熟练掌握一元一次方程的解法步骤是本题的关键；
根据一元一次方程的步骤移项，合并同类项，根据得，即可求出答案．
【详解】解：
移项，得：
合并同类项，得：
x非零实数，
，
，
，
故选：D．
3. 数学老师给所教的名同学各买了一件相同的毕业纪念礼物，扫码支付了元，则每件礼物的价格可表示为（ ）
A. 元B. 元C. 元D. 元
【答案】A
【解析】
【分析】本题考查了列代数式．理解题意是解题的关键．
由题意知，每件礼物的价格可表示为元，然后判断作答即可．
【详解】解：由题意知，每件礼物的价格可表示为元，
故选：A．
4. 嘉淇想知道一张普通打印纸的厚度，她将一包500张的打印纸压实测得厚度为，则一张打印纸的厚度约为（ ）
A. B. C. D.
【答案】D
【解析】
【分析】本题主要考查科学记数法，有理数的除法运算，根据科学记数法的表示方法求解即可．科学记数法的表示形式为的形式，其中，n为整数．解题关键是正确确定a的值以及n的值．
【详解】．
∴一张打印纸的厚度约为．
故选：D．
5. 如图，一张正方形木板，点E，F分别在上，沿锯掉得到五边形，五边形的周长为，正方形的周长为，则下列正确的是（ ）
A. B.
C. D. ，大小无法比较
【答案】C
【解析】
【分析】本题考查了三角形三边关系的应用．熟练掌握三角形中两边之和大于第三边是解题的关键．
根据三角形中两边之和大于第三边，求解作答即可．
【详解】解：由题意知，，，
∵，
∴，
故选：C．
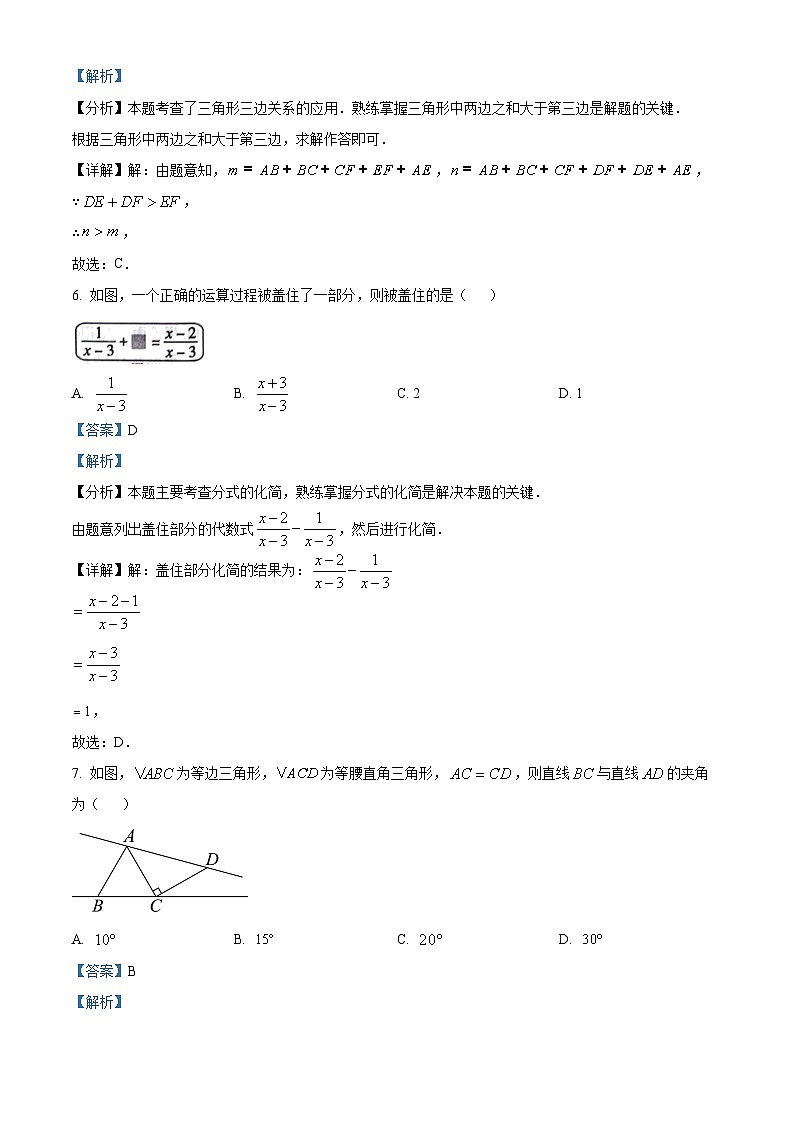
6. 如图，一个正确的运算过程被盖住了一部分，则被盖住的是（ ）
A. B. C. 2D. 1
【答案】D
【解析】
【分析】本题主要考查分式的化简，熟练掌握分式的化简是解决本题的关键．
由题意列出盖住部分的代数式，然后进行化简．
【详解】解：盖住部分化简的结果为：
，
故选：D．
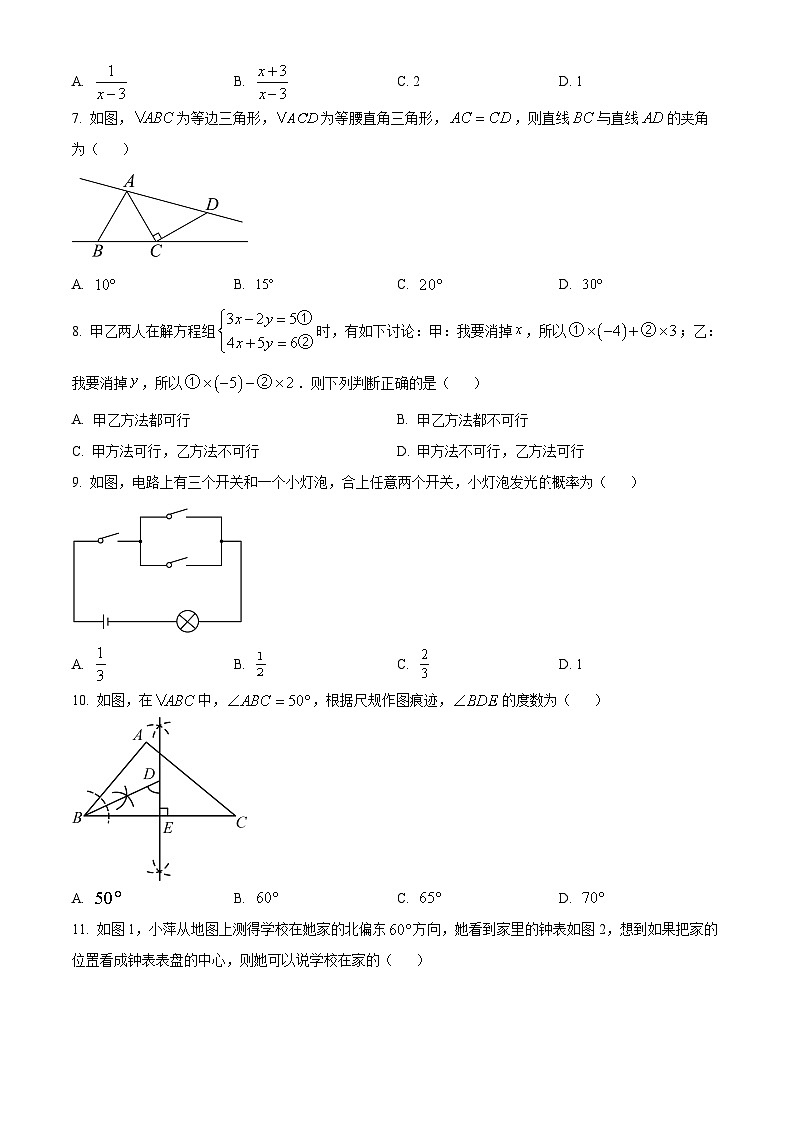
7. 如图，为等边三角形，为等腰直角三角形，，则直线与直线的夹角为（ ）

A. B. C. D.
【答案】B
【解析】
【分析】此题考查了等边三角形和等腰直角三角形的性质，三角形内角和定理，
延长，交于点E，根据题意得到，，然后利用三角形内角和定理求解即可．
【详解】如图，延长，交于点E，

∵为等边三角形，为等腰直角三角形，
∴，
∴
∴直线与直线的夹角为．
故选：B．
8. 甲乙两人在解方程组时，有如下讨论：甲：我要消掉，所以；乙：我要消掉，所以．则下列判断正确的是（ ）
A. 甲乙方法都可行B. 甲乙方法都不可行
C. 甲方法可行，乙方法不可行D. 甲方法不可行，乙方法可行
【答案】A
【解析】
【分析】本题考查加减消元法，根据消掉哪个未知数，就让哪两个未知数的系数的绝对值相等，进行判断即可．
【详解】解：得：；消去了；
，得：；消去了；
故甲，乙的方法都可行；
故选A．
9. 如图，电路上有三个开关和一个小灯泡，合上任意两个开关，小灯泡发光的概率为（ ）

A. B. C. D. 1
【答案】C
【解析】
【分析】本题考查树状图法求概率，根据题意，画出树状图，利用概率公式进行计算即可．
【详解】解：如图，设三个开关分别用表示，

画出树状图如下：
，
共6种等可能的结果，其中小灯泡发光的结果有4种，
∴小灯泡发光的概率为；
故选：C．
10. 如图，在中，，根据尺规作图痕迹，的度数为（ ）

A. B. C. D.
【答案】C
【解析】
【分析】本题考查了作图基本作图，角平分线的定义垂直平分线的性质三角形内角和定理，根据作图，得出平分，然后根据，求出，由垂直平分线，得到，然后利用三角形内角和定理求出结果即可．
【详解】由作图可得，平分，垂直平分线
∵
∴
∵
∴．
故选：C．
11. 如图1，小萍从地图上测得学校在她家的北偏东方向，她看到家里的钟表如图2，想到如果把家的位置看成钟表表盘的中心，则她可以说学校在家的（ ）
A. 1点钟方向B. 2点钟方向C. 7点钟方向D. 8点钟方向
【答案】B
【解析】
【分析】此题考查了方位角，钟面角，
首先求出相邻两个数之间的夹角为，进而根据方位角求解即可．
【详解】∵钟表一圈，共有12个数字，
∴平均分成12份
∴相邻两个数之间的夹角为
∵小萍从地图上测得学校在她家的北偏东方向，
∴她可以说学校在家的2点钟方向．
故选：B．
12. 如图，三角板、量角器和直尺如图摆放，三角板的斜边与半圆相切于点，点B、D、E分别与直尺的刻度1、9、重合，则三角板直角边的长为（ ）
A. B. C. 5D. 6
【答案】D
【解析】
【分析】本题考查了切线的性质，勾股定理，含的直角三角形等知识．熟练掌握切线的性质，勾股定理，含的直角三角形是解题的关键．
由题意知，，，如图，连接，则，，，由勾股定理得，，根据，计算求解即可．
【详解】解：由题意知，，，
如图，连接，
∵三角板的斜边与半圆相切于点，
∴，，，
由勾股定理得，，
∵，
∴，
故选：D．
13. 如图所示的长方体中，棱的长度为，矩形与矩形的面积如图所示，则矩形的面积为（ ）
A. B. C. D.
【答案】B
【解析】
【分析】本题考查了整式混合运算，表示出和的长是解题关键．根据矩形的面积公式，分别求出，，即可得出矩形的面积．
【详解】解：矩形的面积为，，
,，
矩形的面积为,
，
矩形的面积为，
故选：B
14. 甲乙丙三人用同一张矩形纸张接力进行如图所示的操作：甲任意画一个，折叠纸张使得点与点重合，折痕与边交于点；乙再折出射线，点在延长线上；丙再折叠纸张使得落在上，点对应点为点，连接；则下列说法错误的是（ ）
A. 四边形为平行四边形
B. 中，若，则四边形为矩形
C. 若，则四边形为正方形
D. 若射线平分，则四边形为菱形
【答案】C
【解析】
【分析】题目主要考查特殊四边形的判定和性质，根据题意，熟练运用特殊四边形的判定是解题关键
【详解】解：A、根据题意得：，
∴四边形为平行四边形，不符合题意；
B、∵中，若，
∴，
由选项A得四边形为平行四边形，
∴四边形为矩形，不符合题意；
C、∵，
∴ 四边形为矩形，符合题意；
D、∵射线平分，
∴，
由选项A得四边形为平行四边形，即，
∴，
∴，
∴，
∴四边形为菱形，不符合题意；
故选：C
15. 如图1，在某个盛有部分水的容器内放一个小水杯，现在匀速持续地向容器内注水，小水杯内水的高度和注水时间之间的关系如图2所示，则从开始注水至把小水杯注满水需要的时间为（ ）
A. B. C. D.
【答案】C
【解析】
【分析】本题考查一次函数的实际应用，结合图象可知，把小水杯注满水的过程符合一次函数的特征，设函数解析式为，待定系数法求出函数解析式，进而求出时所对应的时间，即可．
【详解】解：由图象可知，把小水杯注满水的过程符合一次函数的特征，设函数解析式为，
则：图象经过，代入解析式得：
，解得：，
∴，
当时，，解得：，
∴从开始注水至把小水杯注满水需要的时间为15s；
故选C．
16. 二次函数的图象与轴交于A，B两点，与轴交于点，顶点为点，则：①；②的面积为；③当时，若，在图象上，则．上述结论正确的个数有（ ）
A. 0个B. 1个C. 2个D. 3个
【答案】C
【解析】
【分析】该题主要考查了二次函数的性质，解题的关键是确定顶点坐标和与轴交点．
根据解析式先确定顶点，和与轴交点，即可确定①②，再根据函数开口方向和对称轴确定③；
【详解】∵，
∴顶点，故①正确；
令，则，
解得：，
，
，故②错误；
对称轴为，当时，离对称轴越近值越小，
∵，
∴故③正确；
故选：C．
二、填空题（本大题共3个小题，共11分.17小题3分，18~19小题每空2分，把答案写在题中横线上）
17. 式子有意义，写出一个符合条件的的整数值：______．
【答案】3(3或4或5中一个即可)
【解析】
【分析】本题考查二次根式有意义的条件，求不等式组的整数解，先根据二次根式有意义的条件，列出不等式组，求解后，写出一个整数值即可．
【详解】解：∵式子有意义，
∴，解得：，
∴符合条件的的整数值为3，4，5；
故答案为：3(3或4或5中一个即可)
18. 嘉淇做动态电路中滑动变阻器的电学实验，电源电压恒定不变，电流与电阻的关系如图所示．
（1）电源电压为______V；
（2）该滑动变阻器的铭牌上标有“”字样，“”表示滑动变阻器连入电路的最大电阻是，“”表示滑动变阻器允许通过的最大电流是，则该滑动变阻器连入电路的最小电阻是______Ω．
【答案】 ①. 3 ②.
【解析】
【分析】本题考查了反比例函数的应用，解题的关键是会利用函数图象求函数解析式．
（1）由图象可知：成反比例函数，当时，，代入公式可得电源电压；
（2）得出函数解析式为，令求得的取值范围即可．
【详解】解：（1）由图象可知：成反比例函数，
当时，，
∴，
故答案为：3；
（2）∵限制电流不超过，
，
根据图象解得，
∵最大电阻为的滑动变阻器，
∴电阻在之间．
故最小电阻为：，
故答案为：3；．
19. 如图，在正六边形内部以为边作正方形，连接．
（1）______；
（2）若，则点到的距离为______．
【答案】 ①. ##30度 ②.
【解析】
【分析】本题考查了正六边形的性质、正方形的性质、等腰三角形的性质、全等三角形的性质和判定，解直角三角形等知识，熟练掌握正六边形的性质和正方形的性质是解题的关键．
（1）由正六边形的性质和正方形的性质即可求解；
（2）过作于，证明，得出，再得出，即可求解；
【详解】解：（1）∵六边形是正六边形，
，
∵四边形是正方形，
∴，
∴，
故答案为：；
（2）如图，过作于，
根据题意得，
同（1）得，
，
，
，
，
．
故答案为：；．
三、解答题（本大题共7个小题，共71分.解答应写出文字说明、证明过程或演算步骤）
20. 如图，是一个正方体展开图，正方体中相对的面上的数字或代数式互为相反数．
（1）试确定和的值；
（2）求的值．
【答案】（1）
（2）2
【解析】
【分析】本题考查了正方体的展开图，相反数的概念，算术平方根．熟练掌握正方体的展开图，相反数的概念，算术平方根是解题的关键．
（1）由题意知，，，进而求解即可；
（2）将和的值代入，计算求解即可．
【小问1详解】
解：由题意知，，，
解得，；
【小问2详解】
解：，
∴的值为2．
21. 现有甲、丙正方形卡片，乙矩形卡片各若干张，卡片的边长如图1所示.同学们分别用若干张卡片拼出其他不重叠无缝隙的图形.

（1）嘉嘉用一张甲和两张乙拼出如图2的图形，面积记为，请你用，表示出面积并求出当，时的值；
（2）琪琪对嘉嘉说，我在你拼的图里再放一张卡片就能拼成一个大正方形.
①琪琪放入的卡片是______（选填“甲”“乙”或“丙”）；
②根据琪琪新拼出的图形面积，可以得到一个等式，请直接写出这个等式.
【答案】（1），
（2）①丙；②
【解析】
【分析】本题考查了完全平方公式的几何应用，解题的关键是列出代数式表示几何图形的面积．
（1）根据题意表示出面积即可，将，代入计算即可求解；
（2）①根据题意即可判断；
②结合正方形的面积即可列出等式．
【小问1详解】
解：，
当，时，．
【小问2详解】
解：①根据题意可得需要放入的卡片是边长为的正方形，
∴放入的卡片是丙．
故答案为：丙．
②正方形边长为，
则正方形的面积为，
故.
22. 某班体育期末测试中有一项为定点投篮，规定每名同学投5次，投中1次记1分，测试时两名同学请假未到校，其余同学的成绩如图所示，
（1）直接写出这些同学投篮成绩的众数和中位数；
（2）规定初中生定点投篮命中率达到为合格，求参加测试的这些同学在该项目中的合格率；
（3）若两名请假的同学补测后发现全班成绩的中位数与众数都发生了变化，直接写出补测的两名同学的成绩．
【答案】（1）众数是4；中位数是4
（2）
（3）3，3
【解析】
【分析】本题主要考查众数和中位数，解题的关键是掌握中位数及众数的概念．
（1）根据中位数及众数的定义即可解答；
（2）根据初中生定点投篮命中率达到为合格确定合格分数，即可解答；
（3）根据中位数及众数的概念逐一判断即可．
【小问1详解】
，
中位数位于第20和21个数，即，
众数是：4；
【小问2详解】
∵定点投篮命中率达到为合格，
∴得分为4分或5分的合格，
∴参加测试的这些同学在该项目中的合格率．
【小问3详解】
两名请假的同学补测后总人数为，
故中位数位于第21和22个数，
∵两名请假的同学补测后发现全班成绩的中位数与众数都发生了变化，
且中位数之前是4，众数也是4，
故当两名请假的同学补测成绩为5，5时，中位数是4，众数是5，不符合；
当两名请假的同学补测成绩为3，3时，中位数是，众数是3和4，符合；
故得出两名请假的同学补测成绩都是3分．
23. 如图1为某游乐场“海盗船”未启动时的示意图，船体为，为地面，为转轴，为船最中间的位置，与交于点，测得，米，转轴到地面的高度为米.
（1）直接写出与的位置关系并求未启动时到地面的高度；
（2）“海盗船”启动后，当或转到与同一高度时开始折返，如图2，船体转到了，船体旋转了多少度？
（3）从在最高点到在最高点，求点经过的路径长度.（参考数据：）
【答案】（1），米
（2）
（3）米
【解析】
【分析】（1）根据在同圆中，等弧所对的圆心角相等可得，根据等腰三角形底边上的高、顶角的角平分线、底边上的中线重合可得，米，根据锐角三角函数的定义可得米，根据直角三角形中两直角边的平方和等于斜边的平方可求得的值，即可求解；
（2）根据题意可得，根据内错角相等，两直线平行可得，根据两直线平行，内错角相等可得，结合题意可得，即可求解；
（3）根据题意可得从在最高点到在最高点，船体旋转了度，结合弧长公式即可求解．
【小问1详解】
解：∵为船最中间的位置，
∴，
则，
∴，米，
∵，
∴米，
则米，
即米，
转轴到地面的高度为米，则未启动时到地面的高度为米．
【小问2详解】
解：根据题意可得，
∴，
∴，
∵，
即，
则，
即船体转到了，船体旋转了度．
【小问3详解】
解：从在最高点到在最高点，船体旋转了度，
则点经过的路径长度为米．
【点睛】本题考查了圆心角、弧、弦的关系，等腰三角形的性质，解直角三角形的应用，勾股定理，平行线的判定和性质，弧长公式等，根据平行线的判定和性质得出旋转角的度数是解题的关键．
24. 如图，在平面直角坐标系中，直线：与轴交于点，直线与轴，轴交于点，点，与交于点，连接，已知的长为4．
（1）求点的坐标及直线的解析式；
（2）求的面积；
（3）若直线上有一点使得的面积等于的面积，直接写出点的坐标．
【答案】（1）；直线的解析式为
（2）
（3）或
【解析】
【分析】本题主要考查了一次函数的性质及三角形面积的计算．
（1）把代入，即可求出坐标，再根据点和用待定系数法即可求出函数解析式；
（2）先求出，再根据图象即可求解；
（3）设，根据或即可求解；
【小问1详解】
解：∵，
∴将点代入得，
∴；
∵的长为4，
∴，
设直线解析式为，
将点和代入得：
，
解得：，
故直线的解析式为；
【小问2详解】
令，得，
∴，
∴．
【小问3详解】
根据题意得：，
设，
令，得，
∴，
如图：
，
解得：，
或，
解得：，
故或．
25. 如图，国家会展中心的大门的截面图是由抛物线和矩形构成的，矩形的边米，米，以所在直线为轴，以所在直线为轴建立平面直角坐标系，抛物线顶点的坐标为．
（1）求此抛物线对应的函数表达式；
（2）近期需要对大门进行粉刷，工人师傅搭建一木板，点正好在抛物线上，支撑垂直轴，米，工人师傅站在木板上，他能刷到的最大垂直高度是米．
①判断工人师傅能否刷到顶点；
②设点是上方抛物线上的一点，且点的横坐标为，直接写出他不能刷到大门顶部的对应点的横坐标的范围．
【答案】（1）
（2）①不能；②
【解析】
【分析】本题主要考查的是二次函数的实际应用，同时考查了待定系数法求解析式，二次函数的性质、应用等知识，熟知二次函数的性质并灵活应用是解题关键．
（1）利用待定系数法即可求出函数表达式；
（2）①先求出点坐标为，再求出直线的解析式为，进而求出，根据师傅能刷到的最大垂直高度是米，比较大小即可解答；
②根据师傅能刷到的最大垂直高度是米，得到当时，他就不能刷到大门顶部，令，得到，解得，结合二次函数性质即可得到他不能刷到大门顶部的对应点的横坐标的范围是．
【小问1详解】
解：由题意知，抛物线顶点的坐标为，
设抛物线的表达式为，
∵，
∴，
将点代入抛物线解析式得，
解得，
∴抛物线对应的函数的表达式为．
【小问2详解】
①将代入中，得，
∴点，
设直线的解析式为，
将点代入得，
∴，
∴直线的解析式为，
过D作x轴的垂线交x轴于点H，交直线于P，
∵点的坐标为，
∴点的横坐标为，
将代入，得，
∴点的坐标为，
∵他能刷到的最大垂直高度是米，
且，
∴工人师傅不能刷到顶点；
②过E作x轴的垂线交直线于点F，
∵点的横坐标为，
∴，，
∴．
∵师傅能刷到的最大垂直高度是，
∴当时，他就不能刷到大门顶部，
当，即时，
解得．
又∵是关于的二次函数，且图象开口向下，
∴他不能刷到大门顶部的对应点的横坐标的范围是．
26. 如图1，在正方形中，E，F分别在边上，且于点．

（1）试猜想线段与的数量关系为______；
（2）数学小组的同学在此基础上进行了深入的探究：
①如图2，在正方形中，若点E，F，G，H分别在边上，且于点，求证：；
②如图3，将①中的条件“在正方形中”改为“在矩形中，，”，其他条件不变，试推理线段与的数量关系；
③如图4，在四边形中，，，，点为的三等分点，连接，过点作，垂足为点，直接写出线段的长．
【答案】（1）
（2）①见详解；②；③或
【解析】
【分析】（1）由“”可证，可得；
（2）①过点作交于，过点作交于，证明即可求解；
②过点作交于，过点作交于，由①可得；
③如图3，过点作于，根据垂直的定义得到，根据已知条件得到或，根据勾股定理得到或，证明，根据相似性质即可得到结论．
【小问1详解】
证明：∵四边形是正方形，
，
，
，
，
，
，
，
．
【小问2详解】
①证明：过点作交于，过点作交于，

∵四边形是正方形，
四边形为矩形，四边形为矩形，
,
∴，
∵，
∴，
∴，
∴，
∴；
②解：；
理由：
过点作交于，过点作交于，

由①可得，，
，
，
，
，
，
；
③解：如图3，过点作于，

，
，
，
点是的三等分点，，
或，
，
或，
，
，
，
，
，
，
∴，
，
，或，
解得或．
【点睛】本题考查了四边形的综合题，正方形的性质，矩形的性质，全等三角形的判定和性质，相似三角形的判定和性质，勾股定理，正确地作出辅助线是解题的关键．