数学28.1 锐角三角函数精品课件ppt

这是一份数学28.1 锐角三角函数精品课件ppt，共14页。PPT课件主要包含了由正弦值求线段的长度，正弦的几种表示方法，新知探究，知识归纳，典例精讲，当堂训练，当堂练习，已知边长求正弦值，已知正弦值求边长，课堂小结等内容，欢迎下载使用。

锐角三角函数---正弦
【问题1】在Rt△ABC中,当∠A=30º时,∠A的对边与斜边有什么数量关系？
【问题2】把Rt△ABC缩小或放大,∠A的对边与斜边的数量关系变了吗？
【问题3】在Rt△ABC中,当∠A=45º,(或∠A=60º或∠A=α),∠A的对边与斜边的比值是定值吗？
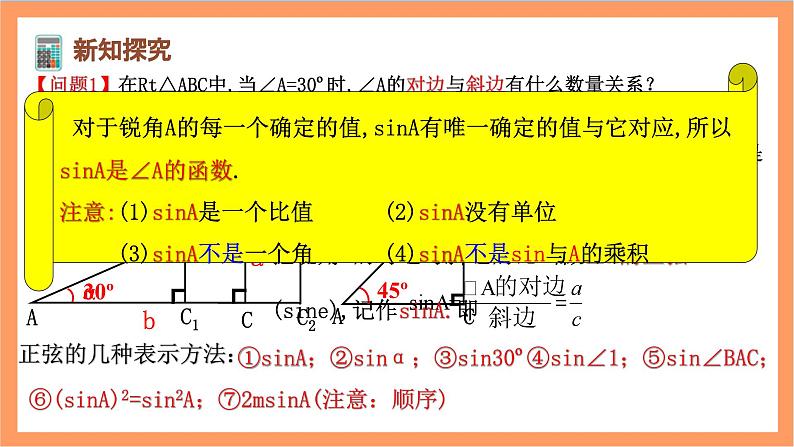
如图,在Rt△ABC中,∠C=90º,我们把锐角A的对边与斜边的比叫做∠A的正弦(sine),记作sinA.即
①sinA；②sinα；③sin30º④sin∠1；⑤sin∠BAC；⑥(sinA)2=sin2A；⑦2msinA(注意：顺序)
对于锐角A的每一个确定的值,sinA有唯一确定的值与它对应,所以sinA是∠A的函数.注意:(1)sinA是一个比值 (2)sinA没有单位 (3)sinA不是一个角 (4)sinA不是sin与A的乘积
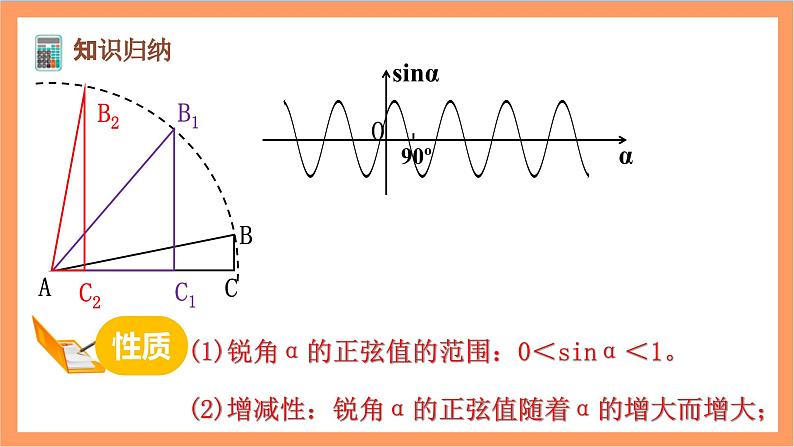
(2)增减性：锐角α的正弦值随着α的增大而增大；
(1)锐角α的正弦值的范围：0＜sinα＜1。
【例1】如图,在Rt△ABC中,∠C=90º,求sinA和sinB的值.
解：如图在Rt△ABC中,由勾股定理得：
∴ AB = 3BC =3×3=9.
1.在Rt△ABC中,∠C=90º,sinA= ,BC=6,则AB的长为( ) A.4 B.6 C.8 D.102.在△ABC中,∠C=90º,如果sinA= ,AB=6,那么BC=___.3.在△ABC中,∠C=90º,AC=24cm,sinA= ,则这个三角形的周长为______.
所以△ABC的周长为:AB+BC+AC=7+24+25=56(cm).
1.在平面直角平面坐标系中,已知点A(3,0)和B(0,-4),则sin∠OAB=____.2.如图,点D(0,3),O(0,0),C(4,0)在⊙A上,BD是⊙A的 一条弦,则sin∠OBD=____.3.用“＞”“＜”“＝”填空：sin15º____sin20º.
解：作BD⊥AC于点D， ∵sinA= ，
又∵△ABC为等腰三角形,BD⊥AC， ∴AC=2AD=6， ∴S△ABC=AC×BD÷2=12.
2.如图,在△ABC中,∠ACB=90º,CD⊥AB. (1)sinB可以由哪两条线段之比表示? (2)若AC=5,CD=3,求sinB的值.
解：(1)∵∠A=∠A,∠ADC=∠ACB=90º， ∴△ACD∽△ABC,∴∠ACD=∠B，