2024年广东省中山市中考一模联考数学试题（原卷版+解析版）

这是一份2024年广东省中山市中考一模联考数学试题（原卷版+解析版），文件包含2024年广东省中山市中考一模联考数学试题原卷版docx、2024年广东省中山市中考一模联考数学试题解析版docx等2份试卷配套教学资源，其中试卷共23页， 欢迎下载使用。

1. 27立方根是（ ）
A. B. C. 3D.
【答案】C
【解析】
【分析】本题主要考查了立方根的概念，熟练掌握立方根的概念是解题的关键．
直接用立方根的定义求解即可．
【详解】解：27立方根是．
故选：C．
2. 在实数，，，中，无理数是（ ）
A. B. C. D. 3.14
【答案】B
【解析】
【分析】根据无理数的特征，即可解答．
【详解】解：在实数，，，中，无理数是，
故选：B．
【点睛】本题考查了无理数的特征，即为无限不循环小数，熟知该概念是解题的关键．
3. 2024年春节，全国文旅一片繁荣，其中哈尔滨用他们的真诚火爆出圈，赢得“南方小土豆”等游客约万人次，将用科学记数法表示为（ ）
A. B. C. D.
【答案】C
【解析】
【分析】本题考查了用科学记数法表示绝对值大于的数，一般形式为，其中，n为整数位数减，据此即可解答．
【详解】解：．
故选：C
4. 计算的结果为（ ）
A. B. C. D.
【答案】A
【解析】
【分析】根据积的乘方计算法则求解即可．
【详解】解：，
故选A．
【点睛】本题主要考查了积的乘方计算，熟知相关计算法则是解题的关键．
5. 若有意义，则x的取值范围是（ ）
A. B. C. D.
【答案】C
【解析】
【分析】本题考查了二次根式有意义的条件，根据二次根式有意义的条件：“被开方数是非负的”可得，进而可求解，熟练掌握二次根式有意义的条件是解题的关键．
【详解】解：依题意得：，
解得：，
故选C．
6. 某同学学习了正方体的表面展开图后，在如图所示的正方体的表面展开图上写下了“传承红色文化”六个字，还原成正方体后，“红”的对面是（ ）

A. 传B. 承C. 文D. 化
【答案】D
【解析】
【分析】正方体的平面展开图中，相对面的特点是之间一定相隔一个正方形，据此作答．
【详解】解：∵正方体的平面展开图中，相对面的特点是之间一定相隔一个正方形，
∴在此正方体上与“红”字相对的面上的汉字是“化”．
故选：D．
【点睛】本题考查了正方体的展开图形，解题关键是从相对面入手进行分析及解答问题．
7. 不等式组的解集是（ ）
A. 无解B. C. D.
【答案】B
【解析】
【分析】本题考查解不等式组，分别求出两个不等式的解集，再找到公共部分即可．
详解】解：解得，
解得，
∴不等式组的解集是，
故选：B．
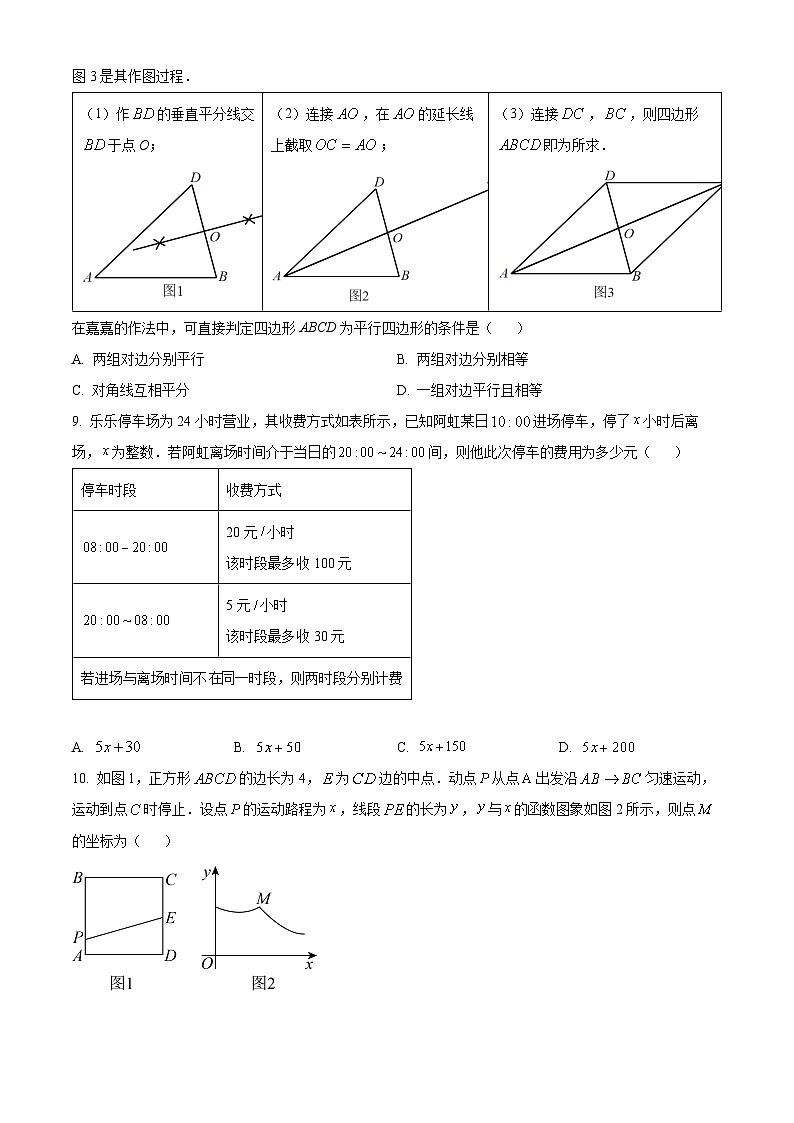
8. 综合实践课上，嘉嘉画出，利用尺规作图找一点C，使得四边形为平行四边形．图1~图3是其作图过程．
在嘉嘉的作法中，可直接判定四边形ABCD为平行四边形的条件是（ ）
A. 两组对边分别平行B. 两组对边分别相等
C. 对角线互相平分D. 一组对边平行且相等
【答案】C
【解析】
【分析】根据作图步骤可知，得出了对角线互相平分，从而可以判断．
【详解】解：根据图1，得出的中点，图2，得出，
可知使得对角线互相平分，从而得出四边形为平行四边形，
判定四边形ABCD为平行四边形的条件是：对角线互相平分，
故选：C．
【点睛】本题考查了平行四边形的判断，解题的关键是掌握基本的作图方法及平行四边形的判定定理．
9. 乐乐停车场为24小时营业，其收费方式如表所示，已知阿虹某日进场停车，停了小时后离场，为整数．若阿虹离场时间介于当日的间，则他此次停车的费用为多少元（ ）
A. B. C. D.
【答案】B
【解析】
【分析】由题意得阿虹停车的时间第一时段超过5小时，且第二个时段的停车时间为小时，则可求解．
【详解】解：阿虹离场时间介于当日的间，
阿虹的停车费为：元．
故选：B．
【点睛】本题主要考查列代数式，解答的关键是理解清楚题意，找到相应的等量关系．
10. 如图1，正方形的边长为4，为边的中点．动点从点出发沿匀速运动，运动到点时停止．设点的运动路程为，线段的长为，与的函数图象如图2所示，则点的坐标为（ ）

A. B. C. D.
【答案】C
【解析】
【分析】证明，，，则当P与A，B重合时，最长，此时，而运动路程为0或4，从而可得答案．
【详解】解：∵正方形的边长为4，为边的中点，
∴，，，
当P与A，B重合时，最长，
此时，
运动路程为0或4，
结合函数图象可得，
故选C
【点睛】本题考查的是从函数图象中获取信息，正方形的性质，勾股定理的应用，理解题意，确定函数图象上横纵坐标的含义是解本题的关键．
二、填空题（共5个小题，每小题4分，满分20分）
11. 计算：的结果为_______．
【答案】1
【解析】
【分析】本题主要考查了二次根式的乘法、平方差公式等知识点，掌握二次根式的乘法法则成为解题的关键．
【详解】解：．
故答案为：1．
12. 若，则___________．
【答案】
【解析】
【分析】根据绝对值的非负性，平方的非负性求得的值进而求得的算术平方根即可求解．
【详解】解：∵，
∴，
解得：，
∴，
故答案为：．
【点睛】本题考查了求一个数的算术平方根，熟练掌握绝对值的非负性，平方的非负性求得的值是解题的关键．
13. 若关于的一元二次方程有两个不相等的实数根，则的取值范围是________．
【答案】且
【解析】
【分析】本题考查了一元二次方程根的判别式与根的关系，熟练掌握根的判别式与根的关系是解答本题的关键，当时，，一元二次方程有两个不相等的实数根；当时，一元二次方程有两个相等的实数根；当时，一元二次方程没有实数根，还要注意二次项系数不等于0．
【详解】解：由题意得：，解得：，
∵，
∴的取值范围是且，
故答案为：且．
14. 如图所示，有一天桥高为5米，是通向天桥的斜坡，，市政部门启动“陡改缓”工程，决定将斜坡的底端C延伸到D处，使，则的长度约为____（保留一位小数，参考数据：，）
【答案】37米##3.7m
【解析】
【分析】本题考查了解直角三角形的应用，解题关键是掌握锐角三角函数定义及特殊三角函数值，根据在中，，得，计算得米，再根据在中，，即可求得的值，然后根据，计算即可得出答案．
【详解】解：在中，米，，，
，
(米)，
在中，，，
，
，
（米），
故答案：3.7米．
15. 如图，四边形ABCD中，AB＝AC＝AD，∠CBD＝15°，BD＝AB，则∠BDC＝_____．
【答案】45°
【解析】
【分析】以A为圆心，AB为半径作，过点A作AM⊥BD于M，分别求出∠ADC，∠ADB可得结论；
【详解】解：如图：以A为圆心，AB为半径作，过点A作AM⊥BD于M，
∵AB=AC=AD，
∴∠CAD=2∠CBD=30°，
∴∠ADC=∠ACD=75°，
∵AB=AD，AM⊥BD，
∴BM=DM，
∵BD=AB，
∴ ，
∴ ，
∴∠ABM=∠ADB=30°，
∴∠BDC=∠ADC-∠ADB=45°，
故答案为：45°．
【点睛】本题考查圆周角定理，等腰三角形的性质，解直角三角形等知识，解题的关键是理解题意，灵活运用所学知识解决问题，属于中考常考题型；
三、解答题（共 4 个小题，每小题 6 分，满分 24 分）
16. 计算：．
【答案】2
【解析】
【分析】本题主要考查了特殊角的三角函数函数值、零次幂、负整数次幂等知识，灵活运用相关运算法则成为解答本题的关键．
先根据特殊角的三角函数函数值、零次幂、负整数次幂化简，然后再计算即可．
【详解】解：
.
17. 化简：．
【答案】
【解析】
【分析】此题考查了分式的混合运算，原式第二项利用除法法则变形，约分后两项通分并利用同分母分式的加法法则计算得到最简结果．
【详解】解：
原式

，
18. 解方程：．
【答案】
【解析】
【分析】去分母化为整式方程，求出方程的根并检验即可得出答案．
【详解】解：原方程可化为．
方程两边同乘，得．
解得．
检验：当时，．
∴原方程的解是．
【点睛】本题考查了分式方程的解法，熟练掌握解分式方程的方法是解题关键．
19. “读书可以让人保持思想活力，让人得到智慧启发，让人滋养浩然之气”．某校为响应全民阅读活动，利用节假日面向社会开放学校图书馆．据统计，第一个月进馆100人次，进馆人次逐月增加，第三个月进馆达到169人次，若进馆人次的月平均增长率相同．求进馆人次的月平均增长率．
【答案】进馆人次的月平均增长率为．
【解析】
【分析】本题主要考查了一元二次方程的实际应用，设进馆人次的月平均增长率为，则第二个月进馆的人次为，第三个月进馆的人次为，据此列出方程求解即可．
【详解】解：设进馆人次的月平均增长率为，
由题意得，，
解得或（舍去），
答：进馆人次的月平均增长率为．
四、解答题（共3个小题，每小题8分，满分24分）
20. 创建文明城市，构建美好家园．为提高垃圾分类意识，幸福社区决定采购A，B两种型号的新型垃圾桶．若购买3个A型垃圾桶和4个B型垃圾桶共需要580元，购买6个A型垃圾桶和5个B型垃圾桶共需要860元．
（1）求两种型号垃圾桶的单价；
（2）若需购买A，B两种型号的垃圾桶共200个，总费用不超过15000元，至少需购买A型垃圾桶多少个？
【答案】（1）A，B两种型号的单价分别为60元和100元
（2）至少需购买A型垃圾桶125个
【解析】
【分析】（1）设两种型号的单价分别为元和元，然后根据题意列出二元一次方程组求解即可；
（2）设购买A型垃圾桶个，则购买A型垃圾桶个，根据题意列出一元一次不等式并求解即可．
【小问1详解】
解：设A，B两种型号的单价分别为元和元，
由题意：，
解得：，
∴A，B两种型号的单价分别为60元和100元；
【小问2详解】
设购买A型垃圾桶个，则购买B型垃圾桶个，
由题意：，
解得：，
∴至少需购买A型垃圾桶125个．
【点睛】本题考查二元一次方程组和一元一次不等式的实际应用，理解题意，找准数量关系，准确建立相应方程和不等式并求解是解题关键．
21. 如图所示，内接于，是的直径，是上的一点，平分，，垂足为，与相交于点．
（1）求证：是的切线；
（2）当的半径为5，时，求的长．
【答案】（1）证明见解析；
（2）4.8
【解析】
【分析】（1）根据“过半径的外端垂直于半径的直线是圆的切线”进行证明；
（2）根据三角函数的意义及勾股定理求解．
本题考查了切线的判定和性质，掌握三角函数的意义及勾股定理是解题的关键．
【小问1详解】
证明：，
，
平分，
，
，
，
，
，
，
是圆的半径，
是的切线；
【小问2详解】
解：是的直径，
，
，
，
，
，
，
解得：，
．
22. 如图，抛物线顶点坐标为，交y轴于点，交x轴于A，B两点，连接，．
（1）求此抛物线的解析式；
（2）点为抛物线在轴下方上一点，若与面积相等，请求出点的坐标．
【答案】（1）；
（2）满足条件点的坐标为，．
【解析】
【分析】本题考查了待定系数法求函数解析式、三角形的面积公式，解本题的关键在于明确题意，利用二次函数性质和数形结合思想解答问题．
（1）设抛物线的解析式为，把代入求解即可；
（2）先求得抛物线与x轴两个交点的坐标，利用三角形面积公式求得的面积，再利用，计算即可求解．
【小问1详解】
解：∵抛物线顶点坐标为，
∴可设抛物线的解析式为，
把代入得，
∴；
【小问2详解】
解：令，
则，
解得，，
∴，，
∴，
∴，
解得，
∵点M在x轴下方，
∴，
∴，
解得，，
∴满足条件的点M的坐标为，．
五、解答题（共2个小题，第23题10分，第24题12分，满分22分）
23. 随着科技的发展，扫地机器人已广泛应用于生活中，某公司推出一款新型扫地机器人，经统计该产品2022年每个月的销售情况发现，每台的销售价格随销售月份的变化而变化、设该产品2022年第（为整数）个月每台的销售价格为（单位：元），与的函数关系如图所示（图中为一折线）．

（1）当时，求每台的销售价格与之间的函数关系式；
（2）设该产品2022年第个月的销售数量为（单位：万台），m与的关系可以用来描述，求哪个月的销售收入最多，最多为多少万元？（销售收入每台的销售价格销售数量）
【答案】（1）
（2）第5个月的销售收入最多，最多为3375万元
【解析】
分析】（1）利用待定系数法即可求解；
（2）根据销售收入每台的销售价格销售数量求得销售收入为万元与销售月份之间的函数关系，再利用函数的性质即可求解．
【小问1详解】
解：当时，设每台的销售价格与之间的函数关系式为．
∵图象过两点，
，解得
∴当时，每台的销售价格与之间的函数关系式为．
【小问2详解】
设销售收入为万元，
①当时，，
，当时，（万元）．
②当时，，
，
∴随的增大而增大，
∴当时，（万元）．
，∴第5个月的销售收入最多，最多为3375万元．
【点睛】本题考查了待定系数法求一次函数的解析式、二次函数在销售问题中的应用，理清题中的数量关系并熟练掌握二次函数的性质是解题的关键．
24. 如图，一次函数的图象与反比例函数的图象相交于点，与轴交于点，与轴交于点．
（1）由图像可知，当x 时，；
（2）求出a，k的值；
（3）若为x轴上的一动点，当的面积为时，求m的值；
（4）在轴上是否存在点，使得，若存在，请直接写出点坐标，若不存在，请说明理由．
【答案】（1）；
（2），；
（3）或11；
（4）的坐标为或．
【解析】
【分析】（1）根据图象求解即可；
（2）将点代入，即可求出的值，从而得到．再将代入，即可求出的值；
（3）根据一次函数解析式可求出，．结合为正轴上的一动点，可求出．最后根据，结合三角形面积公式，即可列出关于的等式，解出的值即可．
（4）过作轴于，作的垂直平分线交轴于，交于，连接，并延长交轴于，分两种情况，利用一次函数的解析式解答即可．
【小问1详解】
根据图像可以看出表示一次函数在双曲线上方部分，
∴当时，；
【小问2详解】
由题意可知点在一次函数的图象上，
，
．
一次函数的图象与反比例函数的图象相交于点，
，
；
【小问3详解】
对于，令，则，
解得：，
．
令，则，
．
为轴的一动点，
，
，
，
，，
，
解得：或．
【小问4详解】
过作轴于，
轴，
，
，，
，
把，代入，
，
作的垂直平分线交轴于，交于，连接，并延长交轴于，
是等腰三角形，
，
，
，
，
，
，
设直线的解析式为：，
把，代入解析式可得：，
解得：，
直线的解析式为：，
把代入，
解得：，
，
综上所述，的坐标为或．
【点睛】本题是反比例函数综合题，考查一次函数与反比例函数图象的交点问题，一次函数与坐标轴的交点问题等知识．利用数形结合的思想是解题关键．
（1）作的垂直平分线交于点O；

（2）连接，在的延长线上截取；

（3）连接，，则四边形即为所求．

停车时段
收费方式
20元小时
该时段最多收100元
5元小时
该时段最多收30元
若进场与离场时间不在同一时段，则两时段分别计费