2024年河北省邯郸市第十三中学九年级中考三模数学试题（原卷版+解析版）

这是一份2024年河北省邯郸市第十三中学九年级中考三模数学试题（原卷版+解析版），文件包含2024年河北省邯郸市第十三中学九年级中考三模数学试题原卷版docx、2024年河北省邯郸市第十三中学九年级中考三模数学试题解析版docx等2份试卷配套教学资源，其中试卷共40页， 欢迎下载使用。
1. 面积为9的正方形，其边长等于（ ）
A. 9的平方根B. 9的算术平方根
C. 9的立方根D. 的算术平方根
【答案】B
【解析】
【分析】根据算术平方根的定义解答即可．
【详解】解：正方形的面积为9，
其边长．
故选：B．
【点睛】本题考查的是算术平方根，解题的关键在于熟练掌握算术平方根的定义，算术平方根：一般地，如果一个正数的平方等于，即，那么这个正数叫做的算术平方根．
2. 将变形正确的是（ ）
A. B.
C. D.
【答案】A
【解析】
【分析】本题考查平方差公式，掌握平方差公式的特点是解题的关键．利用平方差公式求解即可．
【详解】解：原式
，
故选：A．
3. 为防止森林火灾的发生，会在森林中设置多个观测点，如图，点A表示另一处观测台，若，那么起火点M在观测台A的（ ）
A. 南偏东B. 南偏西C. 北偏东D. 北偏西
【答案】B
【解析】
【分析】本题考查了平行线性质以及垂直的定义，先由，得出，结合两直线平行，内错角相等，即可作答．
【详解】解：如图：
∵，
∴，
∵南北方向的直线平行，
∴
∴，
∴，
∴起火点M在观测台A南偏西，
故选：B．
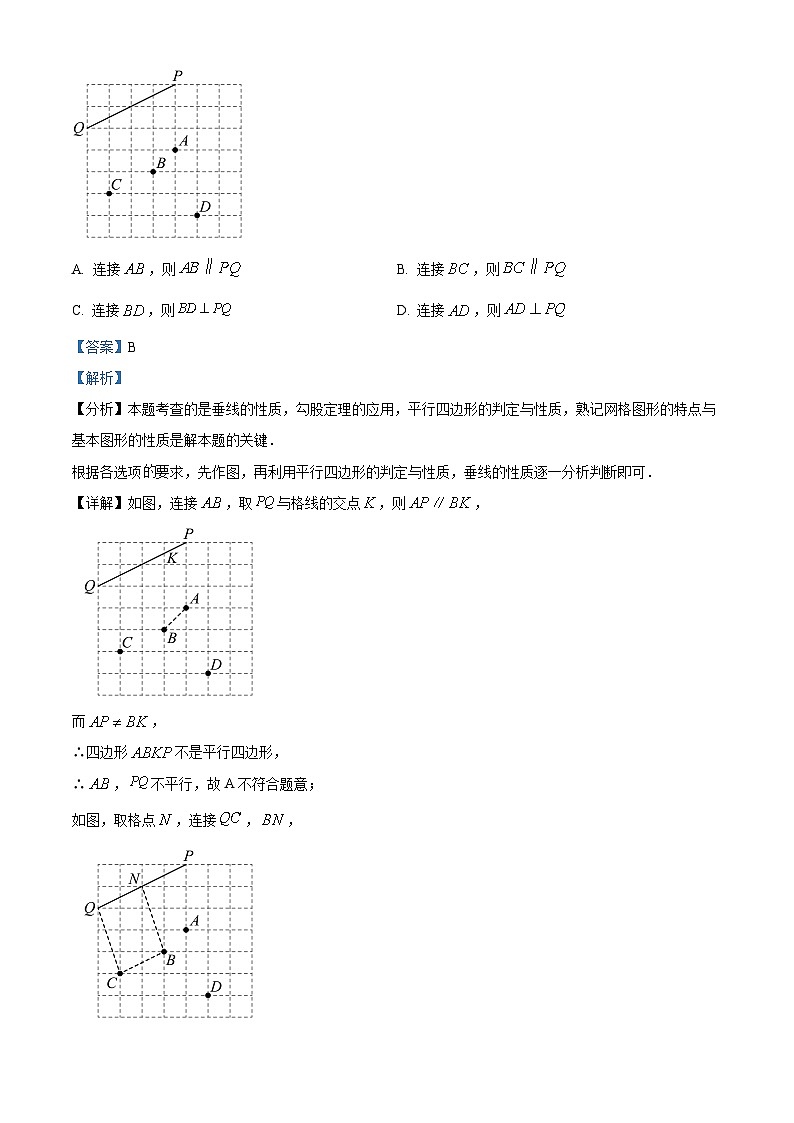
4. 如图，在正方形网格内，线段的两个端点都在格点上，B，C，D四个格点，下面四个结论中正确的是（ ）
A. 连接，则B. 连接，则
C. 连接，则D. 连接，则
【答案】B
【解析】
【分析】本题考查的是垂线的性质，勾股定理的应用，平行四边形的判定与性质，熟记网格图形的特点与基本图形的性质是解本题的关键．
根据各选项要求，先作图，再利用平行四边形的判定与性质，垂线的性质逐一分析判断即可．
【详解】如图，连接，取与格线的交点，则，

而，
∴四边形不是平行四边形，
∴，不平行，故A不符合题意；
如图，取格点，连接，，

由勾股定理可得：，
∴四边形是平行四边形，
∴，故B符合题意；
如图，取格点，

根据网格图的特点可得：，
根据垂线的性质可得：，，都错误，故C，D不符合题意；
故选：B
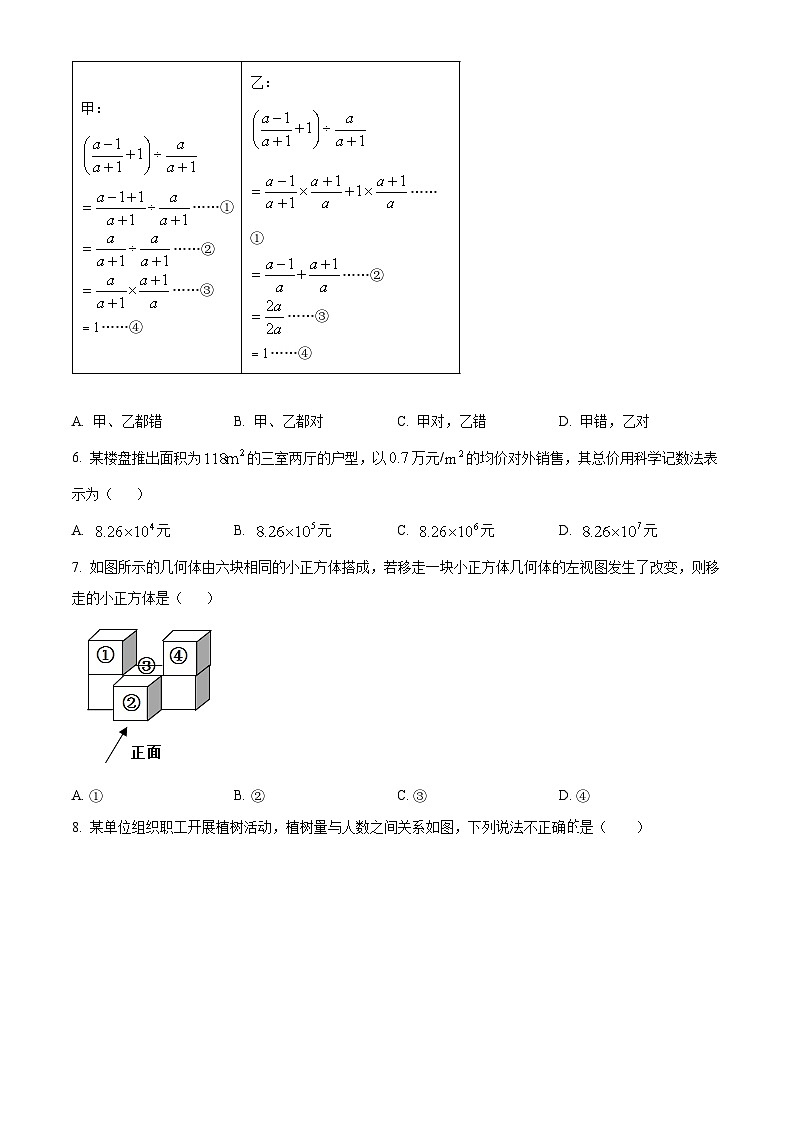
5. 在复习分式的化简运算时，老师把甲、乙两位同学的解答过程分别展示如下．则（ ）
A. 甲、乙都错B. 甲、乙都对C. 甲对，乙错D. 甲错，乙对
【答案】A
【解析】
【分析】本题主要考查分式的混合运算，熟练掌握分式的混合运算法则是解题关键．
根据分式的运算法则，分析甲、乙两位同学的解答过程即可判断．
【详解】解：甲同学的计算错误，
错误原因：第一步计算中，没有通分；
乙同学计算错误，
错误原因：第三步计算中，同分母分式相加，分母应保持不变；
正确的解答如下：
，
∴甲、乙都错，
故选：A．
6. 某楼盘推出面积为的三室两厅的户型，以万元/的均价对外销售，其总价用科学记数法表示为（ ）
A. 元B. 元C. 元D. 元
【答案】B
【解析】
【分析】把一个大于的数记成的形式，其中是整数数位只有一位的数，是正整数，这种记数法叫做科学记数法，由此解答．
【详解】解：万元/元/
元=元，
故选：B．
【点睛】本题考查科学记数法—表示较大的数，是基础考点，掌握相关知识是解题关键．
7. 如图所示的几何体由六块相同的小正方体搭成，若移走一块小正方体几何体的左视图发生了改变，则移走的小正方体是（ ）
A. ①B. ②C. ③D. ④
【答案】B
【解析】
【分析】根据左视图的定义，影响左视图的因素是行数及其行数中小正方体的最高层数，据此判断即可．
【详解】根据几何体，得它的左视图如下，
∵去掉①既没有改变几何体的行数，也没有改变行数中小正方体的最高层数，从而几何体的左视图不会改变，
∴①不符合题意；
∵去掉②改变了几何体的行数，没有改变行数中小正方体的最高层数，从而几何体的左视图改变，
∴②符合题意；
∵去掉③既没有改变几何体的行数，也没有改变行数中小正方体的最高层数，从而几何体的左视图不会改变，
∴③不符合题意；
∵去掉④既没有改变几何体的行数，也没有改变行数中小正方体的最高层数，从而几何体的左视图不会改变，
∴④不符合题意；
故选：B．
【点睛】本题考查了几何体的视图，熟练掌握几何体的三视图的画法和视图的定义是解题的关键．
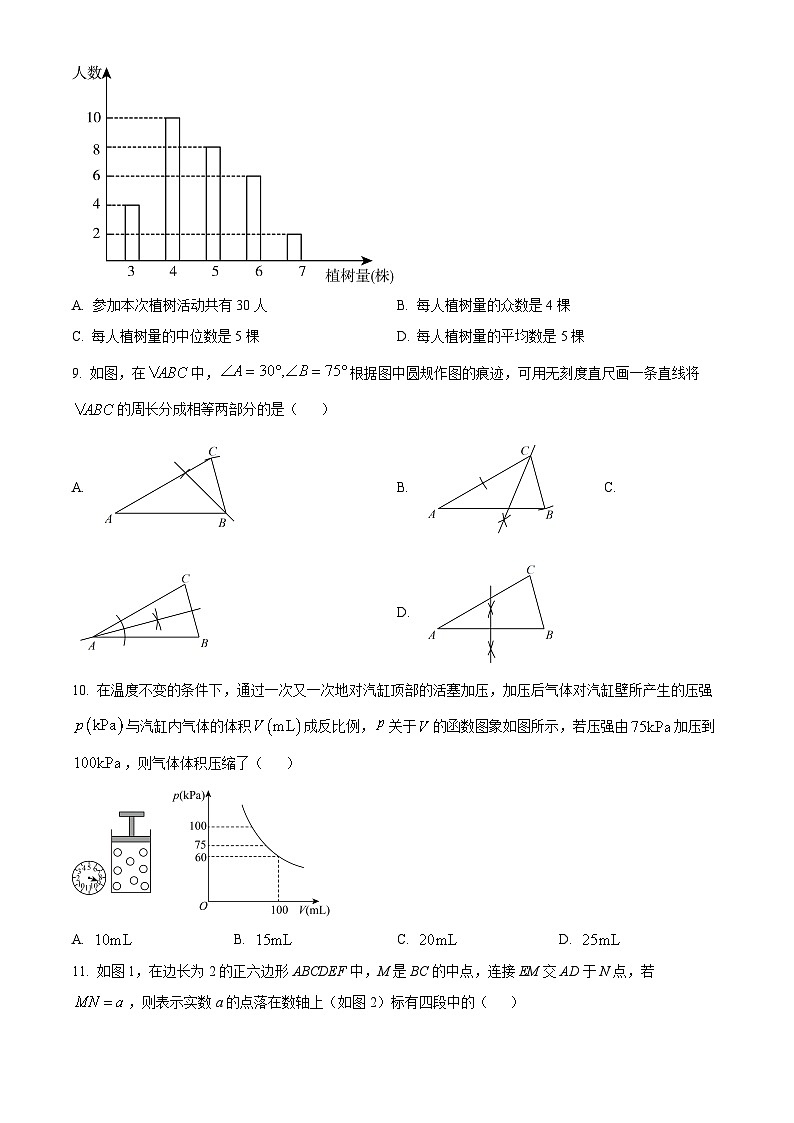
8. 某单位组织职工开展植树活动，植树量与人数之间关系如图，下列说法不正确的是（ ）
A. 参加本次植树活动共有30人B. 每人植树量的众数是4棵
C. 每人植树量的中位数是5棵D. 每人植树量的平均数是5棵
【答案】D
【解析】
【详解】试题解析：A、∵4+10+8+6+2=30（人），
∴参加本次植树活动共有30人，结论A正确；
B、∵10＞8＞6＞4＞2，
∴每人植树量的众数是4棵，结论B正确；
C、∵共有30个数，第15、16个数为5，
∴每人植树量的中位数是5棵，结论C正确；
D、∵（3×4+4×10+5×8+6×6+7×2）÷30≈4.73（棵），
∴每人植树量的平均数约是4.73棵，结论D不正确．
故选D．
考点：1.条形统计图；2.加权平均数；3.中位数；4.众数．
9. 如图，在中，根据图中圆规作图的痕迹，可用无刻度直尺画一条直线将的周长分成相等两部分的是（ ）
A. B. C. D.
【答案】C
【解析】
【分析】根据三角形内角和定理求得，则，根据三线合一即可求解．
【详解】解：∵在中，
∴，
∴，
∴，
则作图为的角平分线，将的周长分成相等两部分，
A选项作图为的角平分线，B选项为的角平分线，不合题意，
C选项为的角平分线，符合题意，
D选项为的垂直平分线，不合题意，
故选：C．
【点睛】本题考查了作角平分线，垂直平分线，等腰三角形的性质与判定，熟练掌握等腰三角形的性质与判定是解题的关键．
10. 在温度不变的条件下，通过一次又一次地对汽缸顶部的活塞加压，加压后气体对汽缸壁所产生的压强与汽缸内气体的体积成反比例，关于的函数图象如图所示，若压强由加压到，则气体体积压缩了（ ）

A. B. C. D.
【答案】C
【解析】
【分析】由图象可得关于的函数解析式为，然后问题可求解．
【详解】解：设关于的函数解析式为，由图象可把点代入得：，
关于的函数解析式为，
当时，则，
当时，则，
压强由加压到，则气体体积压缩了；
故选：C．
【点睛】本题主要考查反比例函数的应用，熟练掌握反比例函数的应用是解题的关键．
11. 如图1，在边长为2的正六边形ABCDEF中，M是BC的中点，连接EM交AD于N点，若，则表示实数a的点落在数轴上（如图2）标有四段中的（ ）
A. 段①B. 段②C. 段③D. 段④
【答案】C
【解析】
【分析】连接BE、CE，CF 根据正多边形的性质求得BE，CE；由平行线分线段成比例求得MN，再由三角形的边长关系得出BE＞ME＞CE即可解答；
【详解】解：如图所示，连接BE、CE，CF，则O为正六边形的中心，
∵正六边形的每个中心角都是60°，
∴每条边和中心构成的三角形都是等边三角形，
∴EB=4，
∵正六边形的每个内角都是120°，
∴△DEC中，∠CDE=120°，∠DCE=∠DEC=30°，
∴∠BCE=120°-30°=90°，
∴Rt△BCE中，BC=2，则，
∵∠OFE=∠AOF=60°，∴AB∥EF，
∵∠OFE=∠OCB=60°，∴BC∥EF，
∴EF∥AD∥BC，
∵BE=2OB，∴ME=2MN，
∵CE＜ME＜BE，即，
∴．
故选： C．
【点睛】本题考查了正多边形与圆的关系，三角形的边长关系，平行线分线段成比例定理，掌握正多边形内角和中心角是解题关键．
12. 已知点在同一个函数图象上，则这个函数图象可能是（ ）
A. B. C. D.
【答案】B
【解析】
【分析】点在同一个函数图象上，可得N、P关于y轴对称，当时，y随x的增大而增大，即可得出答案．
详解】解：∵，
∴得N、P关于y轴对称，
∴选项A、C错误，
∵在同一个函数图象上，
∴当时，y随x的增大而增大，
∴选项D错误，选项B正确．
故选：B．
【点睛】此题考查了函数的图象．注意掌握排除法在选择题中的应用是解此题的关键．
13. 延时课上，王林用四根长度都为的木条制作了图1所示正方形，而后将正方形的边固定，平推成图的图形，并测得，则在此变化过程中结论错误的是( )

A. 长度不变，为B. 长度变小，减少
C. 长度变大，增大D. 面积变小，减少
【答案】D
【解析】
【分析】根据正方形的性质，菱形的性质分别求得面积，，的长度，然后逐项分析判断即可求解．
【详解】连接，，

四边形是正方形，
，，，，
，正方形面积，
，
在菱形中，连接，，过作于点，
，，，
，
是等边三角形，
，，，
菱形面积，
故选项A不符合题意；
，
故选项B不符合题意；
，
故选项C不符合题意；
故选项D符合题意；
故选：D．
【点睛】本题考查了正方形的性质，菱形的性质，勾股定理，熟练掌握正方形与菱形的性质是解题的关键．
14. 如图，△ABC的面积为12，AC＝3，现将△ABC沿AB所在直线翻折，使点C落在直线AD上的C处，P为直线AD上的一点，则线段BP的长可能是（ ）
A. 3B. 5C. 6D. 10
【答案】D
【解析】
【分析】过B作BN⊥AC于N，BM⊥AD于M，根据折叠得出∠C′AB=∠CAB，根据角平分线性质得出BN=BM，根据三角形的面积求出BN，即可得出点B到AD的最短距离是8，得出选项即可．
【详解】
解：如图：
过B作BN⊥AC于N，BM⊥AD于M，
∵将△ABC沿AB所在直线翻折，使点C落在直线AD上的C′处，
∴∠C′AB=∠CAB，
∴BN=BM，
∵△ABC的面积等于12，边AC=3，
∴×AC×BN=12，
∴BN=8，
∴BM=8，
即点B到AD的最短距离是8，
∴BP的长不小于8，
即只有选项D符合，
故选D．
【点睛】本题考查的知识点是折叠的性质，三角形的面积，角平分线性质的应用，解题关键是求出B到AD的最短距离，注意：角平分线上的点到角的两边的距离相等．
15. 如图．抛物线与x轴交于点和点，与y轴交于点C．下列说法：①；②抛物线的对称轴为直线；③当时，；④当时，y随x的增大而增大；⑤（m为任意实数）其中正确的个数是（ ）

A. 1个B. 2个C. 3个D. 4个
【答案】C
【解析】
【分析】根据抛物线开口向下，与y轴交于正半轴，可得，根据和点可得抛物线的对称轴为直线，即可判断②；推出，即可判断①；根据函数图象即可判断③④；根据当时，抛物线有最大值，即可得到，即可判断⑤．
【详解】解：∵抛物线开口向下，与y轴交于正半轴，
∴，
∵抛物线与x轴交于点和点，
∴抛物线对称轴为直线，故②正确；
∴，
∴，
∴，故①错误；
由函数图象可知，当时，抛物线的函数图象在x轴上方，
∴当时，，故③正确；
∵抛物线对称轴为直线且开口向下，
∴当时，y随x的增大而减小，即当时，y随x的增大而减小，故④错误；
∵抛物线对称轴为直线且开口向下，
∴当时，抛物线有最大值，
∴，
∴，故⑤正确；
综上所述，正确的有②③⑤，
故选C．
【点睛】本题主要考查了抛物线的图象与系数的关系，抛物线的性质等等，熟练掌握抛物线的相关知识是解题的关键．
16. 如图，在边长为1的菱形中，，将沿射线的方向平移得到，分别连接，，，则的最小值为（ ）
A. 1B. C. D. 2
【答案】C
【解析】
【分析】根据菱形的性质得到，，根据平移的性质得到，，推出四边形是平行四边形，得到，于是得到的最小值的最小值，根据平移的性质得到点在过点且平行于的定直线上，作点关于定直线的对称点，连接交定直线于，则的长度即为的最小值，求得，得到，于是得到结论
【详解】解：在边长为1的菱形中，，
，，
将沿射线的方向平移得到，
，，
四边形是菱形，
，，
，
，，
四边形是平行四边形，
，
的最小值的最小值，
点在过点且平行于的定直线上，
作点关于定直线的对称点，连接交定直线于，
则的长度即为的最小值，
在中，
，，
，，
，
，
，
，
作，
过点D作垂足为G
在中，
．
故选：．
【点睛】
本题考查了轴对称最短路线问题，菱形的性质，矩形的判定和性质，解直角三角形，平移的性质，求得的最小值的最小值是解题的关键．
二、填空题（本大题共3个小题，共10分，17小题2分，18、19小题各4分，每空2分）
17. 如图，正六边形内接于，点在上，点是的中点，则的度数为 ________．
【答案】##45度
【解析】
【分析】本题考查了正多边形与圆，圆周角定理，熟练运用其定理是解题的关键．
先求出正六边形的中心角，再利用圆周角定理求解即可．
【详解】解：如图，连接、、、，
∵正六边形是的内接正六边形，
，
∵点是的中点，
，
，
．
故答案为：．
18. 如图，用两个边长为的小正方形纸片剪拼成一个大的正方形，
（1）则大正方形的边长是 _____cm；
（2）若将此大正方形纸片的局部剪掉，_____（填“能”或“否”）剩下一个长宽之比为且面积为的长方形纸片．
【答案】 ①. 6 ②. 否
【解析】
【分析】本题考查了算术平方根的应用，能根据题意正确列出算式是解题关键．
（1）大正方形的边长就是小正方形的对角线，求小正方形对角线即可；
（2）根据长方形长宽之比为和面积求出长和宽，与正方形边长进行比较即可．
【详解】解：（1）由大正方形的面积，
得大正方形的边长；
故答案为：6；
（2）设长方形纸片长为，宽为，
则，
得，
故，
故不能使剩下一个长宽之比为且面积为的长方形纸片．
故答案为：否．
19. 如图，的三个顶点都在方格纸的格点上，其中点A的坐标是，现将绕点A顺时针旋转得．写出点的坐标是 __________；若函数（，k为常数）的图象经过点，且P为该函数图象上的动点，当P在直线的上方且的面积为时，则P点的横坐标为 __________________．

【答案】 ①. ②. ##
【解析】
【分析】本题考查了旋转的性质和反比例函数k值的几何意义，根据旋转的性质得到点的坐标，根据反比例函数k值的几何意义计算出点P的坐标即可．
【详解】如图所示，即是绕点A顺时针旋转后的图形，则的坐标是；
反比例函数过点，
，
反比例函数解析式为：，
作轴垂足D，轴垂足为E，设，

，
，
整理得，
解得（舍），
，
点P的横坐标为：，
故答案为：，．
三、解答题（本大题共7个小题，共72分，解答应写出文字说明、证明过程或演算步骤）
20. 按如图程序进行运算．如果结果不大于10，就把结果作为输入的数再进行第二次运算，直到符合要求（结果大于10）
（1）当输入的数是10时，请求出输出的结果；
（2）当输入的数是x时，经过第二次运算，结果即符合要求，请求出x的最小整数值．
【答案】（1）16 （2）6
【解析】
【分析】本题主要考查了解一元一次不等式组，与程序流程图有关的计算：
（1）把10代入计算，若结果大于10则输出，若结果不大于10则计算的结果当做输入的输重新计算直至结果大于10输出即可；
（2）根据题意可得第一次输入计算的结果不大于10，把第一次计算的结果作为新输输入，计算的结果大于10，据此列出不等式组求解即可．
【小问1详解】
解：输入10时，计算的结果为，
∴输出的结果为16；
【小问2详解】
解：由题意得，，
解得，
∴x的最小整数值是6．
21. 在矩形中，的长度为a，的长度为，将矩形进行如图所示顺序的折叠，第三步折叠后，点C与点D的对应点分别为，．
（1）①若点落在点下方，则 ；（用含a，b的代数式表示）
②若点，重合，求的值；
（2）如果b的值保持不变，改变a的值，且点始终落在点下方．若四边形的面积的最大值为3，求b的值
【答案】（1）①；②
（2）
【解析】
【分析】（1）①根据折叠的性质推出，，再用可得；
②令，变形可得；
（2）列出，根据二次函数的最值得到当时，最大，结合最大值为3即可求出b值．
【小问1详解】
①由折叠可得：，
，
若点落在点下方，
则；
②若点，，重合，
则，
∴，
∴；
【小问2详解】
如图所示，
∵点始终落在点下方，
∴，
∵b的值保持不变，改变a的值，
∴当时，最大，
∴，整理得：，
解得：（负值舍去）．
【点睛】本题考查了矩形的性质，折叠问题，二次函数的最值，解题的关键是结合折叠的性质表示线段的长度，并且能灵活运用二次函数的最值计算．
22. 一个不透明的袋子中装有四个小球，这四个小球上各标有一个数字，分别是1，1，2，3，这些小球除标有的数字外都相同．
（1）从袋中随机摸出一个小球，则摸出的这个小球上标有的数字是1的概率为 ；
（2）先从袋中随机摸出一个小球，记下小球上标有的数字后，放回，摇匀，再从袋中随机摸出一个小球，记下小球上标有的数字，请利用画树状图或列表的方法、求摸出的这两个小球上标有的数字之积是偶数的概率．
【答案】（1）
（2）
【解析】
【分析】（1）根据题意和题目中的数据，可以计算出从袋中机摸出一个小球，则摸出的这个小球上标有的数字是1的概率；
（2）根据题意可以画出相应的树状图，然后即可求出摸出的这两个小球上标有的数字之积是偶数的概率．
【小问1详解】
由题意可得，数字1，1，2，3中，数字1有2个，
所以，从袋中机摸出一个小球，则摸出的这个小球上标有的数字是1的概率为，
故答案为：；
【小问2详解】
树状图如下：

由上可得，一共有16种等可能性，其中两数之积是偶数的可能性有7种，
摸出的这两个小球上标有的数字之积是偶数的概率．
【点睛】本题考查列表法与树状图法、概率公式，解答本题的关键是明确题意，画出相应的树状图，求出相应的概率．
23. 某校“综合与实践”小组的同学把“民心河护坡的调研与计算”作为一项课题活动，利用课余时间完成了实践调查，并形成了如下活动报告．请根据活动报告计算和的长度（结果精确到0.1m，参考数据：，）．
【答案】的长度约为1.4m，的长度约为4.2m
【解析】
【分析】本题考查了矩形的判定与性质，解直角三角形，关键是构造适当的辅助线便于在直角三角形中求得相关线段．
过点E作，在中求出和的长，在中求出和的长，再求即可．
【详解】解：过点E作，垂足为F，
由题意得：，，
在中，，
∴，
，
∴，
∵，
∴，
∵，
∴，
在中， ，
，
∴，
∴的长度约为1.4m，的长度约为4.2m．
24. 如图，中，，，轴，，抛物线（）的顶点为M，与y轴交点为N．
（1）设P为中点，直接写出直线的函数表达式 ．
（2）求点N最高时的坐标；
（3）抛物线有可能经过点C吗？请说明理由；
（4）在L的位置随t的值变化而变化的过程中，求点M在内部所经过路线的长．
【答案】（1）
（2）
（3）抛物线不可能经过点C
（4）
【解析】
【分析】本题是二次函数的综合题，求一次函数解析式，一元二次方程根的判别式等知识，关键是掌握二次函数的基本性质．
（1）由题意知，点的坐标为，点的坐标为，得点的坐标为，进而利用待定系数法可得直线的函数表达式；
（2）中令，得出关于的二次函数，根据二次函数的性质得出最大值即可；
（3）先求出点的坐标，将点坐标代入二次函数解析式，得出关于的一元二次方程，再根据一元二次方程判别式的正负判断；
（4）由，知顶点，所以点在内部所经过路线的长即为的长，即可求解．
【小问1详解】
∵，，轴，，
∴点的坐标为，点的坐标为，
又为的中点，
∴点的坐标为，
设直线的函数表达式为，
代入，得，，解得：，
∴直线的函数表达式为，
故答案为：；
【小问2详解】
当时，
即的最大值为，
点最高时的坐标为 ；
【小问3详解】
抛物线不可能经过点C，
理由：把，代入，
得，化简为，
，
方程没有实数根，即抛物线不可能经过点；
【小问4详解】
由，知顶点，
在的位置随的值变化而变化的过程中，点都在直线上移动，且经过直线上的点，，
点在内部所经过路线的长为的长度，
即：点在内部所经过路线的长为．
25. 如图，一段铁路的示意图，段和段都是高架桥，段时隧道，，，，在段高架桥上又一盏吊灯，当火车驶过时，灯光可垂直照射到车身上，已知火车甲沿方向迅速行驶，当火车甲经过吊灯时，灯光照射到火车甲上的时间是，火车甲通过隧道的时间为，如果从车尾经过点A时开始计时，设行驶的时间为，车头与点B的距离为．
（1）火车甲的速度和火车甲的长度；
（2）求y关于x的函数解析式（写出x的取值范围），并求当x为何值时，车头差500米到达D点．
（3）若长度相等的火车乙以相同的速度沿方向行驶，且火车甲乙不在隧道内会车（会车时两车均不在隧道内），火车甲先进隧道，火车乙的车头能否到达D点？若能到达，至多驶过地点多少？若不能到达，至少距离D点多少米？说明理由．
【答案】（1）火车甲的速度是，火车甲的长是
（2）当时，车头差500米未到达D点
（3）当火车甲车头到达A点时，火车乙车头不能到达D点
【解析】
【分析】本题考查一次函数的应用以及二元一次方程组的应用，关键是根据题意列出函数解析式．
(1)设火车甲的速度是火车甲的长是， 由题意得二元一次方程组，求解即可；
(2)分类车头到达点前、车头在点时、车头经过点后三种情况写函数解析式，并求出时的值即可；
(3)先求出甲火车从车头到达点，到车尾离开隧道所用时间，再求出乙火车在这段时间内所走路程，从而求出两车不在隧道内会车，乙距离点的距离．
【小问1详解】
设火车甲的速度是，火车甲的长是，
由是题意得：，
解得：，
答：火车甲的速度是，火车甲的长是；
【小问2详解】
当车头到达B点前，即时，；
当车头在B点时，，
当车头经过B点后，即时，
，
综上，，
当车头差500米未到达D点时，，即
解得：，
所以当时，车头差500米未到达D点；
【小问3详解】
火车甲从车头到达点，到车尾离开隧道，共用时，
因此要使两列火车不在隧道内会车，则当火车甲车头到达点时，火车乙的车头距点至少要有的车程，也就是，
，
所以当火车甲车头到达点时，火车乙车头不能到达点， 至少距离点．
26. 如图，在Rt△ABC中，∠ACB＝90°，AB=10，BC＝6，点O在射线AC上（点O不与点A重合），垂足为D，以点O为圆心，分别交射线AC于E、F两点，设OD＝x．
（1）如图1，当点O为AC边的中点时，求x的值；
（2）如图2，当点O与点C重合时，连接DF；求弦DF的长；
（3）当半圆O与BC无交点时，直接写出x的取值范围．
【答案】（1）；（2）；（3）满足条件的x取值范围为：0＜x＜3或x＞12．
【解析】
【分析】（1）先求出OA，再判断出，得出比例式求出x的值，即可得出结论；
（2）先利用等面积求出x知，再判断出，进而求出DH，OH，最后用勾股定理求出DF，即可得出结论；
（3）分两种情况：点O在边AC上和在AC的延长线上，找出分界点，求出x值，即可得出结论．
【详解】（1）在Rt△ABC中，AB＝10，
根据勾股定理得，，
∵点O为AC边的中点，
∴AO＝AC＝，
∵OD⊥AB，∠ACB＝90°，
∴∠ADO＝∠ACB，
又∵∠A＝∠A，
∴．
∴，
∴，
∴．
（2）如图，过点D作DH⊥AC于H，
∵点O与点C重合，
∴S△ABC＝OD•AB＝，
即10x＝8×6，
∴．
∵DH⊥AC于H，
∴∠DHO＝∠ACB＝90°，
∴∠DOH+∠BOD＝∠BOD+∠ABC，
∴∠DOH＝∠ABC，
∴．
∴，
∴，
∴，．
∵OF＝OD＝，
∴FH＝OH+OF＝．
∴在Rt△DFH中，根据勾股定理得，
∴．
（3）如图，当点O在边AC上，且半圆O与AB，
∴OC＝OD＝x，
∴AO＝AC﹣OC＝8﹣x，
∵∠ADO＝∠ACB＝90°，∠A＝∠A，
∴，
∴，
∴，
∴x＝3，
∴0＜x＜3，
如图，当点O在AC的延长线上，且半圆O与AB，
∴OC＝OD＝x，
∴AO＝AC+OC＝8+x，
∵∠ADO＝∠ACB＝90°，∠A＝∠A，
∴，
∴，
∴，
∴x＝12，
即满足条件的x取值范围为：0＜x＜3或x＞12．
【点睛】此题是圆的综合题，主要考查了勾股定理，相似三角形的判定和性质，用分类讨论的思想和方程的思想解决问题是解本题的关键．甲：
……①
……②
……③
……④
乙：
……①
……②
……③
……④
课题
民心河护坡的调研与计算
调查方式
资料查阅、实地查看了解
调查内容
功能
护坡是用来保护河岸，阻止河岸崩塌或冲刷的构筑物
材料
所需材料为石料、混凝土等
护坡时剖面图

相关数据及说明：图中，点A，B，C，D，E在同一竖直平面内，和均与地面平行，岸墙于点A，，，，，
计算结果
…
…
…