2023-2024学年重庆市忠县花桥中学七年级（下）第一次月考数学试卷（含解析）

这是一份2023-2024学年重庆市忠县花桥中学七年级（下）第一次月考数学试卷（含解析），共20页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

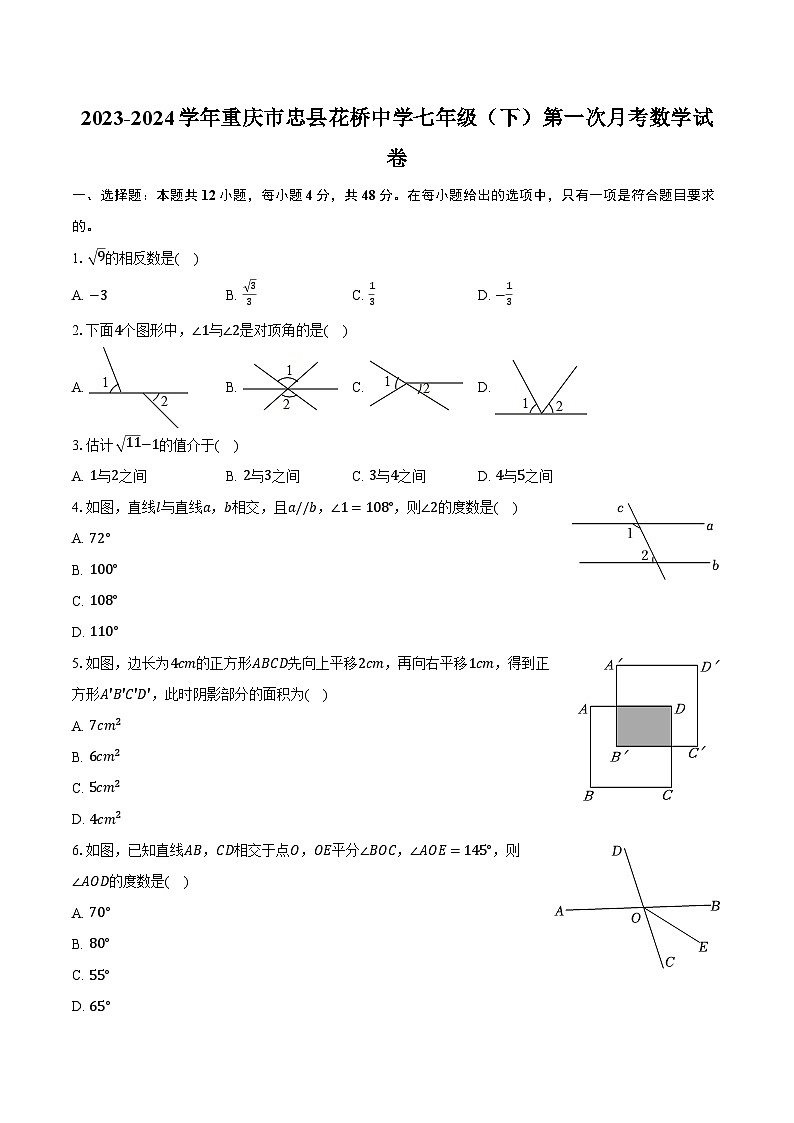
1. 9的相反数是( )
A. −3B. 33C. 13D. −13
2.下面4个图形中，∠1与∠2是对顶角的是( )
A. B. C. D.
3.估计 11−1的值介于( )
A. 1与2之间B. 2与3之间C. 3与4之间D. 4与5之间
4.如图，直线l与直线a，b相交，且a/​/b，∠1=108°，则∠2的度数是( )
A. 72°
B. 100°
C. 108°
D. 110°
5.如图，边长为4cm的正方形ABCD先向上平移2cm，再向右平移1cm，得到正方形A′B′C′D′，此时阴影部分的面积为( )
A. 7cm2
B. 6cm2
C. 5cm2
D. 4cm2
6.如图，已知直线AB，CD相交于点O，OE平分∠BOC，∠AOE=145°，则∠AOD的度数是( )
A. 70°
B. 80°
C. 55°
D. 65°
7.下列各式中，正确的是( )
A. (−3)2=−3B. − 32=−3C. (−3)2=±3D. 32=±3
8.如图，在△ABC中，∠ACB=90°，CD⊥AB，垂足为点D，则图中能表示点到直线距离的垂线段共有( )
A. 2条B. 3条C. 4条D. 5条
9.如图，把一块直角三角尺的直角顶点放在直尺的一边上，若∠1=55°，则∠2的度数为( )
A. 35°B. 45°C. 55°D. 25°
10.如图，把一张对边互相平行的纸条沿EF折叠，若∠EFB=32°，则下列结论：①∠C′EF=32°；②∠AEC=116°；③∠BGE=64°；④∠BFD=116°.其中正确的有( )
A. 1个
B. 2个
C. 3个
D. 4个
11.下列说法：① (−10)2=−10；②数轴上的点与实数成一一对应关系；③一个数的算术平方根仍是它本身，这样的数有三个；④任何实数不是有理数就是无理数；⑤两个无理数的和还是无理数；⑥无理数都是无限小数，正确的个数有( )
A. 2个B. 3个C. 4个D. 5个
12.如图，AE/​/CF，∠ACF的平分线交AE于点B，G是CF上的一点，∠GBE的平分线交CF于点D，且BD⊥BC，下列结论：①BC平分∠ABG；②AC/​/BG；③与∠DBE互余的角有2个；④若∠A=α，则∠BDF=180°−α2；其中正确的有( )
A. ①②B. ②③④C. ①②④D. ①②③④
二、填空题：本题共6小题，每小题4分，共24分。
13.计算： 4−327= ______．
14.若(a+1)2+ b−2=0，则a−b的值为______．
15.命题“如果|a|=|b|，那么a=b”是______命题.(填“真”或“假”)
16. 2−1的相反数是______，|3.14−π|=______．
17.若 2a−2与|b+2|互为相反数，则(a−b)2的平方根=______．
18.①如图1，AB/​/CD，则∠A+∠E+∠C=180°；②如图2，AB/​/CD，则∠E=∠A+∠C；③如图3，若AB/​/EF，则∠x=180°−∠α−∠γ+∠β；④如图4，AB/​/CD，则∠A=∠C+∠P.以上结论正确的是______．
三、解答题：本题共8小题，共78分。解答应写出文字说明，证明过程或演算步骤。
19.(本小题8分)
计算：
(1)(−1)3+|1− 2|+38；
(2)3(−5)3+(−3)2− 25+| 3−2|+( 3)2．
20.(本小题8分)
(1)25(x+1)2−36=0
(2)(2x−1)3=−8．
21.(本小题10分)
已知2a−1的平方根是±3，b−9的立方根是2，c是 12的整数部分．
(1)求a、b、c的值；
(2)若x是 12的小数部分，求x− 12+12的值．
22.(本小题10分)
如图，直线EF，CD相交于点O，OC平分∠AOF，∠AOE=2∠BOD．
(1)若∠AOE=40°，求∠DOE的度数；
(2)猜想OA与OB之间的位置关系，并证明．
23.(本小题10分)
如图，已知AD⊥BC，EF⊥BC，垂足分别为D、F，∠2+∠3=180°，试说明：∠GDC=∠B.请补充说明过程，并在括号内填上相应的理由．
解：∵AD⊥BC，EF⊥BC(已知)，
∴∠ADB=∠EFB=90° ______，
∴AD/​/EF ______．
∴ ______+∠2=180° ______
∵∠2+∠3=180°(已知)．
∴∠1=∠3 ______．
∴AB/​/ ______
∴∠GDC=∠B ______．
24.(本小题10分)
已知：如图，∠A=∠ADE，∠C=∠E．
(1)若∠EDC=3∠C，求∠C的度数；
(2)求证：BE/​/CD．
25.(本小题10分)
新定义：符号“f”表示一种新运算.它对一些数的运算结果如下：
f(−2)=−2−1=−3，
f(−1)=−1−1=−2，
f(0)=0−1=−1，
f(1)=1−1=0，
f(2)=2−1=1，
……
新定义：符号“g”表示一种新运算，它对一些数的运算结果如：
g(−13)=3，
g(−12)=2，
g(12)=−2，
g(13)=−3，
……
利用以上规律计算：
(1)f(−10)= ，g(110)= ；
(2)f(−2015)+g(−12016)= ；
(3)计算：f(x2)−f(xy−y2)+g(1x2−xy)+g(1y2−2)．
26.(本小题12分)
已知AB/​/CD，点M、N分别是AB、CD上的点，点G在AB、CD之间，连接MG、NG．
(1)如图1，若GM⊥GN，求∠AMG+∠CNG的度数；
(2)如图2，若点P是CD下方一点，MG平分∠BMP，ND平分∠GNP，已知∠BMG=32°，求∠MGN+∠MPN的度数；
(3)如图3，若点E是AB上方一点，连接EM、EN，且GM的延长线MF平分∠AME，NE平分∠CNG，2∠MEN+∠MGN=105°，求∠AME的度数
答案和解析
1.【答案】A
【解析】解： 9=3，
∴ 9的相反数是−3，
故选：A．
根据算术平方根和相反数的概念求即可．
本题考查了算术平方根，相反数，熟练掌握这些知识是解题的关键．
2.【答案】B
【解析】解：根据对顶角的定义可知：只有B项中的是对顶角，其它都不是．
故选：B．
根据对顶角的定义，两条直线相交后所得的只有一个公共顶点且两边互为反向延长线，这样的两个角叫做对顶角．
本题考查了对顶角的定义，熟记对顶角的定义是解题的关键．
3.【答案】B
【解析】解：∵ 9< 11< 16，
∴3< 11<4，
∴2< 11−1<3，
∴估计 11−1的值介于2与3之间．
故选：B．
利用二次根式的性质，得出 9< 11< 16，进而得出答案．
此题主要考查了估计无理数的大小，得出 9< 11< 16是解题关键．
4.【答案】A
【解析】解：∵a/​/b，∠1=108°，
∴∠2=180°−∠1=72°．
故选：A．
直接根据平行线的性质即可得出结论．
本题考查的是平行线的性质，用到的知识点为：两直线平行，同旁内角互补．
5.【答案】B
【解析】解：如图，设AD与A′B′交于点E，
∵将边长为4cm的正方形ABCD先向上平移2cm，再向右平移1cm，
∴A′E=2cm，AE=1cm，
∴B′E=2cm，DE=3cm，
∴阴影部分的面积=2×3=6cm2，
故选：B．
由平移的性质可得A′E=2cm，AE=1cm，可求B′E=2cm，DE=3cm，即可求解．
本题考查了正方形的性质，平移的性质，掌握平移的性质是解题的关键．
6.【答案】A
【解析】解：∵∠AOE=145°，
∴∠BOE=180°−∠AOE=35°，
∵OE平分∠BOC，
∴∠BOC=2∠BOE=70°，
∴∠AOD=∠BOC=70°，
故选：A．
先根据补角的定义求出∠BOE，再根据角平分线的定义求出∠BOC，最后根据∠AOD=∠BOC进行求解．
本题考查角平分线的定义，对顶角的性质，补角的定义，熟练掌握对顶角相等是解题的关键．
7.【答案】B
【解析】解：∵ (−3)2=|−3|=3，
∴A选项的结论不正确；
∵− 32=−3，
∴B选项的结论正确；
∵ (−3)2=|−3|=3，
∴C选项的结论不正确；
∵ 32=3，
∴D选项的结论不正确，
故选：B．
利用二次根式的性质对每个选项进行逐一判断即可得出结论．
本题主要考查了二次根式的性质，正确利用二次根式的性质对每个选项进行判断是解题的关键．
8.【答案】D
【解析】【分析】
本题考查了点到直线的距离，理解点到直线的距离是解决本题的关键．
根据点到直线的距离的定义，得结论．
【解答】
解：点C到AB的距离是线段CD的长度，
点B到CD的距离是线段BD的长度，
点A到CD的距离是线段AD的长度，
点A到CB的距离是线段CA的长度，
点B到AC的距离是线段BC的长度，
故选：D．
9.【答案】A
【解析】解：如图，
∵AB/​/CD，
∴∠1=∠3=55°，
∴∠2=180°−90°−55°=35°，
故选：A．
利用平行线的性质可得∠3的度数，再利用平角定义可得答案．
此题主要考查了平行线的性质，关键是掌握两直线平行，同位角相等．
10.【答案】D
【解析】解：①∵AE/​/BG，∠EFB=32°，
∴∠C′EF=∠EFB=32°，故本小题正确；
②∵AE//BG，∠EFB=32°，
∴∠C′EF=∠EFB=32°，
∴∠AEC=180°−∠C′EF−∠EFB=116°，故本小题正确；
③∵∠C′EF=32°，
∴∠GEF=∠C′EF=32°，
∴∠C′EG=∠C′EF+∠GEF=32°+32°=64°，
∵AC′//BD′，
∴∠BGE=∠C′EG=64°，故本小题正确；
④∵∠BGE=64°，
∴∠CGF=∠BGE=64°，
∵DF/​/CG，
∴∠BFD=180°−∠CGF=180°−64°=116°，故本小题正确．
故选：D．
根据平行线的性质及翻折变换的性质对各小题进行逐一分析即可．
本题考查的是平行线的性质及翻折变换的性质，熟知图形翻折不变性的性质是解答此题的关键．
11.【答案】B
【解析】解：① (−10)2=10，故说法错误；
②数轴上的点与实数成一一对应关系，故说法正确；
③一个数的算术平方根仍是它本身，这样的数有0和1两个，故说法错误；
④实数分为有理数和无理数两类，所以任何实数不是有理数就是无理数，故说法正确；
⑤两个无理数的和可能是有理数，也可能是无理数，如 2与− 2的和是0，是有理数，故说法错误；
⑥无理数都是无限小数，故说法正确．
故正确的是②④⑥共3个．
故选：B．
①根据算术平方根的性质即可判定；
②根据实数与数轴上的点的对应关系即可判定；
③根据算术平方根的定义即可判定；
④根据实数的分类即可判定；
⑤根据无理数的性质即可判定；
⑥根据无理数的定义即可判断．
此题主要考查了有理数、无理数、实数的定义及其关系．有理数都可以化为小数，其中整数可以看作小数点后面是零的小数，分数可以化为有限小数或无限循环小数；无理数是无限不循环小数，其中有开方开不尽的数，如 2， 33等，π也是无理数．
12.【答案】C
【解析】解：∵BD⊥BC，
∴∠CBD=90°，
∴∠ABC+∠EBD=90°，
∵∠GBE的平分线交CF于点D，
∴∠DBG=∠EBD，
∴∠ABC=∠CBG，
∴BC平分∠ABG，
∴①正确，
∵AE/​/CF，
∴∠GBC=∠ABC=∠ACB，
∴AC/​/BG，
∴②正确，
∵∠DBE=∠DBG，
∴与∠DBE互余的角有∠ABC，∠GBC，∠ACB，∠GCB，有4个，
∴③错误，
∵∠BDF=180°−∠BDG，∠BDG=90°−∠CBG=90°−∠ACB，
又∵∠ACB=12×(180°−α)=90°−α2，
∴∠BDF=180°−[90°−(90°−α2)]=180°−α2，
∴④正确，
故选：C．
根据平行线的性质得出∠A和∠ACB的关系，再根据角平分线的性质找出图中相等的角，由等角的余角相等即可得出结论．
本题主要考查平行线的性质和判定，关键是要牢记平行线的三个性质，即两直线平行，同位角相等，两直线平行，内错角相等，两直线平行，同旁内角互补．
13.【答案】−1
【解析】解：原式=2−3=−1，
故答案为：−1．
利用算术平方根及立方根的定义计算即可．
本题考查实数的运算，熟练掌握相关运算法则是解题的关键．
14.【答案】−3
【解析】解：由题意得，a+1=0，b−2=0，
解得，a=−1，b=2，
则a−b=−3，
故答案为：−3．
根据非负数的性质列出方程求出a、b的值，代入所求代数式计算即可．
本题考查了非负数的性质：几个非负数的和为0时，这几个非负数都为0．
15.【答案】假
【解析】解：如果|a|=|b|，那么a=b或a=−b，故原命题是假命题，
故答案为：假．
分析是否为真命题，需要分别分析题设是否能推出结论，可得答案．
本题考查了命题与定理，主要考查命题的真假判断，正确的命题叫真命题，错误的命题叫做假命题．
16.【答案】1− 2 π−3.14
【解析】解： 2−1的相反数是−( 2−1)=1− 2，
∵π>3.14，
∴3.14−π<0，
∴|3.14−π|=−(3.14−π)=π−3.14．
故答案为：1− 2，π−3.14．
利用相反数，绝对值的代数意义计算即可求出所求．
此题考查了实数的运算，熟练掌握绝对值及相反数的性质是解本题的关键．
17.【答案】±3
【解析】解：∵若 2a−2与|b+2|互为相反数，
∴ 2a−2+|b+2|=0，
∵ 2a−2≥0，|b+2|≥0，
∴2a−2=0，b+2=0，
∴a=1，b=−2，
∴(a−b)2=9，
∴9的平方根为±3．
故答案为±3．
利用非负数的性质确定a、b的值即可解决问题．
本题考查非负数的性质，有理数的混合运算等知识，解题的关键是熟练掌握非负数的性质．
18.【答案】②③④
【解析】解：①如图1，过点E作EF/​/AB，
∵AB/​/CD，
∴AB//EF//CD，
∴∠A+∠AEF=180°，∠C+∠CEF=180°，
∴∠A+∠AEC+∠C=∠A+∠AEF+∠C+∠CEF=180°+180°=360°，则①错误；
②如图2，过点E作EF/​/AB，
∵AB/​/CD，
∴AB//EF//CD，
∴∠A=∠AEF，∠C=∠CEF，
∴∠A+∠C=∠CEF+∠AEF=∠AEC，则②正确；
③如图3，过点C作CD/​/AB，延长AB到G，
∵AB/​/EF，
∴AB//EF//CD，
∴∠DCF=∠EFC，
由②的结论可知∠GBH+∠HCD=∠BHC，
又∵∠GBH=180°−∠ABH，∠HCD=∠HCF−∠DCF
∴180°−∠ABH+∠HCF−∠DCF=∠BHC，
∴180°−∠ABH+∠HCF−∠EFC=∠BHC，
∴180°−∠α+∠β−∠γ=∠x，故③正确；
④如图4，
过点P作PF/​/AB，
∵AB/​/CD，
∴AB//PF//CD，
∴∠A=∠APF，∠C=∠CPF，
∴∠A=∠CPF+∠APC=∠C+∠APC，则④正确；
故答案为：②③④．
①过点E作EF/​/AB，由平行线的性质即可得出结论；
②过点点E作EF/​/AB，由平行线的性质即可得出结论；
③如图3，过点C作CD/​/AB，延长AB到G，由平行线的性质可得出180°−∠ABH+∠HCF−∠EFC=∠BHC；
④过点P作PF/​/AB，由平行线的性质可得出∠A=∠CPF+∠APC=∠C+∠APC．
本题考查的是平行线的性质，根据题意作出辅助线是解答此题的关键．
19.【答案】解：(1)原式=−1+ 2−1+2
= 2；
(2)原式=−5+9−5+2− 3+3
=4− 3．
【解析】(1)先算乘方，开方，再去绝对值符号，合并同类项解；
(2)先算乘方，开方，再去绝对值符号，从左到右依次计算即可．
本题考查实数的运算，熟练掌握立方根、平方根、绝对值的计算方法是解题关键．
20.【答案】解：(1)25(x+1)2−36=0，
25(x+1)2=36，
(x+1)2=3625，
x+1=±65，
x=0.2或x=−2.2；
(2)(2x−1)3=−8，
2x−1=−2，
2x=−1，
x=−12．
【解析】(1)先移项，系数化为1，再根据开平方法进行解答；
(2)可用直接开立方法进行解答．
本题考查了平方根和立方根的概念．注意一个正数有两个平方根，它们互为相反数；0的平方根是0；负数没有平方根．立方根的性质：一个正数的立方根是正数，一个负数的立方根是负数，0的立方根是0．
21.【答案】解：(1)∵2a−1的平方根是±3，b−9的立方根是2，
∴2a−1=9，b−9=8，
解得：a=5，b=17，
∵9<12<16，
∴3< 12<4，
∴ 12的整数部分是3，
∴c=3，
∴a的值为5，b的值为17，c的值为3；
(2)∵ 12的整数部分是3，
∴ 12的小数部分是 12−3，
∴x= 12−3，
∴x− 12+12
= 12−3− 12+12
=9，
∴x− 12+12的值为9．
【解析】(1)利用平方根，立方根的意义可得2a−1=9，b−9=8，从而可得a=5，b=17，然后再估算出 12的值的范围，从而求出c的值，即可解答；
(2)利用(1)的结论求出x的值，然后把x的值代入式子中进行计算即可解答．
本题考查了估算无理数的大小，平方根，熟练掌握估算无理数的大小是解题的关键．
22.【答案】解：(1)∵∠AOE=40°，
∴∠AOF=180°−∠AOE=140°，
∵OC平分∠AOF，
∴∠COF=12∠AOF=70°，
∴∠DOE=∠COF=70°；
(2)OA⊥OB，
证明过程如下：
设∠AOE=2α°，
则∠AOF=180°−∠AOE=180°−2α°．
∵OC平分∠AOF，
∴∠COF=12∠AOF=90°−α°．
∴∠DOE=∠COF=90°−α°．
∵∠AOE=2∠BOD=2α°，
∴∠BOD=α°．
∴∠BOE=∠DOE−∠BOD=90°−α°−α°=90°−2α°．
∴∠AOB=∠BOE+∠AOE=90°−2α°+2α°=90°．
∴OA⊥OB．
【解析】(1))根据邻补角的定义，由∠AOE=40°，得∠AOF=180°−∠AOE=140°.根据角平分线的定义，由OC平分∠AOF，得∠COF=12∠AOF=70°.根据对顶角的定义，得∠DOE=∠COF=70°．
(2)根据邻补角的定义，设∠AOE=2α°，则∠AOF=180°−∠AOE=180°−2α°.根据角平分线的定义，由OC平分∠AOF，得∠COF=12∠AOF=90°−α°.根据对顶角的定义，得∠DOE=∠COF=90°−α°.由∠AOE=2∠BOD=2α°，得∠BOD=α°，从而推断出∠BOE=∠DOE−∠BOD=90°−α°−α°=90°−2α°，那么∠AOB=90°．
本题主要考查对顶角以及邻补角、角平分线的定义、角的和差关系，熟练掌握对顶角以及邻补角、角平分线的定义、角的和差关系是解决本题的关键．
23.【答案】垂直的定义 同位角相等，两直线平行 ∠1 两直线平行，同旁内角互补 同角的补角相等 DG 两直线平行，同位角相等
【解析】解：∵AD⊥BC，EF⊥BC(已知)，
∴∠ADB=∠EFB=90°(垂直的定义)，
∴AD/​/EF (同位角相等，两直线平行)．
∴∠1+∠2=180°(两直线平行，同旁内角互补)，
∵∠2+∠3=180°(已知)．
∴∠1=∠3(同角的补角相等)．
∴AB/​/DG(内错角相等，两直线平行)，
∴∠GDC=∠B(两直线平行，同位角相等)．
故答案为：垂直的定义；同位角相等，两直线平行；∠1；两直线平行，同旁内角互补；同角的补角相等；DG；两直线平行，同位角相等．
根据平行线的判定和性质，垂直的定义，同角的补角相等知识一一判断即可．
本题考查平行线的判定和性质，解题的关键是熟练掌握基本知识，属于中考常考题型．
24.【答案】解：(1)∵∠A=∠ADE，
∴AC/​/DE，
∴∠EDC+∠C=180°，
又∵∠EDC=3∠C，
∴4∠C=180°，
即∠C=45°；
(2)∵AC/​/DE，
∴∠E=∠ABE，
又∵∠C=∠E，
∴∠C=∠ABE，
∴BE/​/CD．
【解析】(1)根据两直线平行，同旁内角互补，即可得出∠C的度数；
(2)根据AC/​/DE，∠C=∠E，即可得出∠C=∠ABE，进而判定BE/​/CD．
本题主要考查了平行线的性质以及判定的运用，解题时注意：两直线平行，内错角相等；两直线平行，同旁内角互补．
25.【答案】−11 −10 0
【解析】解：(1)f(−10)=−10−1=−11；g(110)=−10．
故答案为：−11，−10；
(2)原式=−2015−1+2016=0．
故答案为：0；
(3)原式=x2−1−(xy−y2−1)+xy−x2+2−y2
=x2−1−xy+y2+1+xy−x2+2−y2
=2．
(1)根据题中给出的例子进行计算即可；
(2)先计算出f(−2015)及g(−12016)的值，再进行计算即可；
(3)先计算出各式的值，再进行计算即可．
本题考查的是有理数的混合运算，熟知有理数混合运算的法则是解题的关键．
26.【答案】解：(1)如图1，过G作GH/​/AB，
∵AB/​/CD，
∴GH/​/AB/​/CD，
∴∠AMG=∠HGM，∠CNG=∠HGN，
∵MG⊥NG，
∴∠MGN=∠MGH+∠NGH=∠AMG+∠CNG=90°；
(2)如图2，过G作GK/​/AB，过点P作PQ/​/AB，设∠GND=α，
∵GK/​/AB，AB/​/CD，
∴GK//CD，
∴∠KGN=∠GND=α，
∵GK/​/AB，∠BMG=32°，
∴∠MGK=∠BMG=32°，
∵MG平分∠BMP，
∴∠GMP=∠BMG=32°，
∴∠BMP=64°，
∵PQ/​/AB，
∴∠MPQ=∠BMP=2∠BMG=64°，
∵ND平分∠GNP，
∴∠DNP=∠GND=α，
∵AB/​/CD，
∴PQ/​/CD/​/GK，
∴∠QPN=∠DNP=∠KGN=α，
∴∠MGN=∠MGK+∠KGN=32°+α，∠MPN=∠MPQ−∠QPN=64°−α，
∴∠MGN+∠MPN=32°+α+64°−α=96°；
(3)如图3，过G作GK/​/AB，过E作ET/​/AB，设∠AMF=x，∠GND=y，
∵AB，FG交于M，MF平分∠AME，
∴∠FME=∠FMA=∠BMG=x，
∴∠AME=2x，
∵GK/​/AB，
∴∠MGK=∠BMG=x，
∵ET/​/AB，
∴∠TEM=∠AME=2x，
∵CD//AB，AB/​/KG，
∴GK//CD，
∴∠KGN=∠GND=y，
∴∠MGN=x+y，
∵∠CND=180°，NE平分∠CNG，
∴∠CNG=180°−y，∠CNE=12∠CNG=90°−12y，
∵ET/​/AB，AB/​/CD，
∴ET/​/CD，
∴∠TEN=∠CNE=90°−12y，
∴∠MEN=∠TEN−∠TEM=90°−12y−2x，∠MGN=x+y，
∵2∠MEN+∠MGN=105°，
∴2(90°−12y−2x)+x+y=105°，
∴x=25°，
∴∠AME=2x=50°．
【解析】(1)过G作GH/​/AB，依据两直线平行，内错角相等，即可得到∠AMG+∠CNG的度数；
(2)过G作GK/​/AB，过点P作PQ/​/AB，设∠GND=α，利用平行线的性质以及角平分线的定义，求得∠MGN=32°+α，∠MPN=64°−α，即可得到∠MGN+∠MPN=32°+α+64°−α=96°；
(3)过G作GK/​/AB，过E作ET/​/AB，设∠AMF=x，∠GND=y，利用平行线的性质以及角平分线的定义，可得∠MEN=∠TEN−∠TEM=90°−12y−2x，∠MGN=x+y，再根据2∠MEN+∠G=105°，即可得到2(90°−12y−2x)+x+y=105°，求得x=25°，即可得出∠AME=2x=50°．
本题主要考查了平行线的性质与判定的综合运用，解决问题的关键是作辅助线构造内错角，利用平行线的性质以及角的和差关系进行推算．