

山西省大同市2022-2023学年七年级下学期4月期中教学质量监测数学试卷(含部分解析)
展开七年级数学
注意事项:
1.本试卷共6页,满分120分,考试时间120分钟.
2.答卷前,考生务必将自己的姓名、准考证号填写在本试卷相应的位置.
3.答案全部在答题卡上完成,答在本试卷上无效.
4.考试结束后,将本试卷和答题卡一并交回.
第I卷 选择题(共30分)
一、选择题(本大题共10个小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项符合题目要求,请选出并在答题卡上将该项涂黑)
1.9的平方根是( )
A.B.C.3D.
2.下列四个点在平面直角坐标系中位于第二象限内的是( )
A.B.C.D.
3.下列各数是无理数的是( )
A.B.C.D.
4.如图,梯子的各条横杆互相平行,,则的度数是( )
A.B.C.D.
5.如图,点在直线上,,,则的度数是( )
A.B.C.D.
6.下列命题是真命题的是( )
A.互补的两个角是邻补角B.两个锐角的和一定是锐角
C.同位角相等D.对顶角相等
7.将两块含角的三角尺按如图所示的方式摆放(两直角边在同一条直线上),可以画出两条互相平行的直线,.这样操作的依据是( )
A.两直线平行,同位角相等B.同位角相等,两直线平行
C.两直线平行,内错角相等D.内错角相等,两直线平行
8.已知,,则( )
A.B.C.D.
9.如图,在平面直角坐标系中,点的坐标是,点的坐标是,将线段平移得到线段.已知平移后点的对应点的坐标是,则点的对应点的坐标是( )
A.B.C.D.
10.将一副三角尺按如图所示的方式放置,给出下列结论:①若,则;②若,则;③;④若,则.其中正确的是( )
A①②③B①②④C.①③④D.①②③④
第Ⅱ卷 非选择题(共90分)
二、填空题(本大题共5个小题,每小题3分,共15分.请将正确答案填在答题卡中的横线上)
11.的相反数为________.
12.在平面直角坐标系中,点,的坐标分别为,,则的长为________.
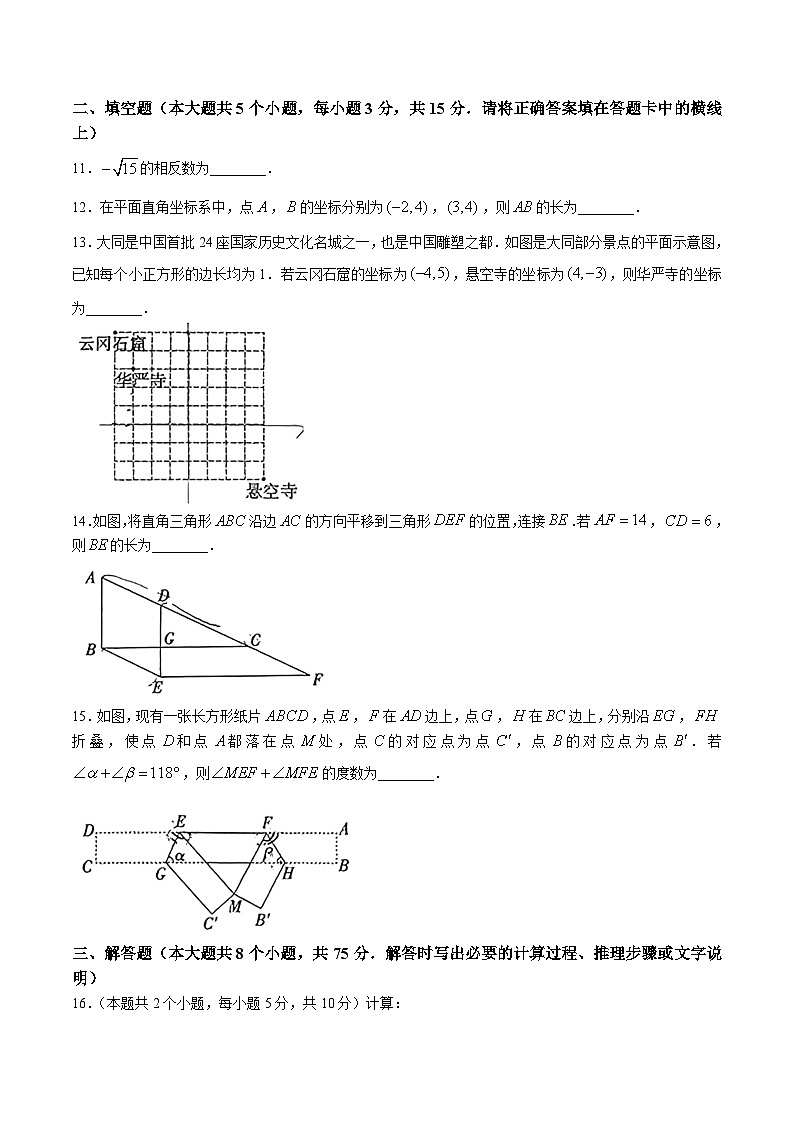
13.大同是中国首批24座国家历史文化名城之一,也是中国雕塑之都.如图是大同部分景点的平面示意图,已知每个小正方形的边长均为1.若云冈石窟的坐标为,悬空寺的坐标为,则华严寺的坐标为________.
14.如图,将直角三角形沿边的方向平移到三角形的位置,连接.若,,则的长为________.
15.如图,现有一张长方形纸片,点,在边上,点,在边上,分别沿,折叠,使点和点都落在点处,点的对应点为点,点的对应点为点.若,则的度数为________.
三、解答题(本大题共8个小题,共75分.解答时写出必要的计算过程、推理步骤或文字说明)
16.(本题共2个小题,每小题5分,共10分)计算:
(1);(2).
17.(本题6分)如图,直线,相交于点,于点,,.求证:是的平分线.
18.(本题7分)某公司为了满足员工的用水需求,把原来容积为的长方体储水箱换成了比原来容积的2倍大的正方体储水箱,求正方体储水箱内部的棱长.
长方体储水箱 正方体储水箱
19.(本题7分)如图,三角形三个顶点的坐标分别是,,.
(1)直接写出点的坐标,并过点画出的平行线;
(2)把三角形向右平移7个单位长度,再向上平移2个单位长度后得到三角形,画出平移后的三角形,并写出点的坐标.
20.(本题10分)完成下面的证明.
如图,在三角形中,于点,点,,分别在边,,上,且,与互补.求证:.
证明:,
________(________).
________(________).
与互补,
(补角的定义).
________(等量代换).
________(________).
________(________)
,
(垂直的定义).
________(等量代换).
.
21.(本题10分)阅读材料,完成下列任务:
材料一:我们可以用以下方法表示无理数的小数部分.
,,即..
的整数部分为1.的小数部分为.
材料二:我们可以用以下方法求无理数的近似值.
面积为107的正方形的边长是,且,
设,其中.
画出边长为的正方形,如图:
根据图中面积,得.
当较小时,忽略,得.解得..
任务:
(1)利用材料一中的方法,求的小数部分;
(2)利用材料二中的方法,探究的近似值.(画出示意图、标明数据,并写出求解过程)
22.(本题12分)如图,,.
图1 图2
(1)如图1,直接写出与之间的数量关系________.
(2)如图2,写出与之间的数量关系,并说明理由.
(3)经过上述探究,可得出结论:如果一个角的两边与另一个角的两边分别平行,那么这两个角________.
(4)已知与的两边分别平行,且比的3倍小,求的度数.
23.(本题13分)如图,在平面直角坐标系中,,,,且轴于点,,满足.
(1)求点,的坐标;
(2)若和的平分线交于点,求的度数;
(3)若点在坐标轴的正半轴上运动,当三角形的面积等于三角形的面积时,直接写出点的坐标.
2022—2023学年第二学期期中教学质量监测
七年级数学参考答案及评分标准
一、选择题(每小题3分,共30分)
1-5:ABDCB6-10:DDBAD
二、填空题(每小题3分,共15分)
11.12.513.14.4
15.
三、解答题(本大题共8个小题,共75分)
16.解:(1)原式(3分)
.(5分)
(2)原式(3分)
.(5分)
17.证明:,(1分)
.(2分)
,.(3分)
.(4分)
.(5分)
是的平分线.(6分)
18.解:设正方体储水箱内部的棱长为.(1分)
根据题意,得.(4分)
解得.(6分)
答:正方体储水箱内部的棱长为.(7分)
19.解:(1)点的坐标是.(1分)
如图,直线即为所求.(3分)
(2)如图,三角形即为所求.(6分)
点的坐标是.(7分)
20.解:(1分)
同位角相等,两直线平行(2分)
(3分)
两直线平行,内错角相等(4分)
(5分)
(6分)
同旁内角互补,两直线平行(7分)
(8分)
两直线平行,同位角相等(9分)
(10分)
21.解:(1),,即.(2分)
的整数部分为9.(3分)
的小数部分为.(4分)
(2)面积为5的正方形的边长是,且(5分)
设,其中.
画出边长为的正方形,如图:(7分)
根据图中面积,得.(8分)
当较小时,忽略,得.解得.(10分)
22.解:(1)(2分)
(2).(3分)
理由:如图:
,
.(4分)
,.(5分)
.(6分)
(3)相等或互补(8分)
(4)由题意,得.(9分)
分两种情况讨论:
①当时,.解得.
.(10分)
②当时,.解得.
.(11分)
综上所述,的度数是或.(12分)
23.解:(1),
,.(1分)
解得,.
点的坐标是,点的坐标是.(3分)
轴,点的坐标是.(4分)
(2)如图,过点作,则.(6分)
轴,.
由题意知,.(7分)
,.
.(8分)
和的平分线交于点,
,.
.∠
.(10分)
(3)点的坐标是或(13分)
部分试题答案解析
5.,.
,.
.
9.由题意,得线段的平移方式是向左平移4个单位长度,向上平移2个单位长度,所以点的对应点的坐标是,即.
10.由题意,知,,,.
,.
.
,故①正确.
,.
,故②正确.
,,
,故③正确.
,,..
,故④正确.
14.由平移的性质,得.
.
.
15.由题意,得.
,.
.
由折叠,得,.
.
22.(1)如图,设与交于点.
,.
,,.
23.(3),,,,
,,,.
三角形的面积为.
分两种情况讨论:
当点在轴的正半轴上时,设点的坐标是,则.
三角形的面积为,.解得.点的坐标是
当点在轴的正半轴上时,设点的坐标是,则.
三角形的面积为..解得.点的坐标是.
综上所述,点的坐标是或.
山西省吕梁市交城县2022-2023学年七年级下学期期中教学质量监测数学试卷(含解析): 这是一份山西省吕梁市交城县2022-2023学年七年级下学期期中教学质量监测数学试卷(含解析),共14页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
山西省大同市2022-2023学年八年级上学期期末教学质量抽样监测数学试卷(解析版): 这是一份山西省大同市2022-2023学年八年级上学期期末教学质量抽样监测数学试卷(解析版),共15页。试卷主要包含了考试结束后,将答题卡交回等内容,欢迎下载使用。
山西省大同市2022-2023学年八年级下学期期末教学质量抽样监测数学试卷(含解析): 这是一份山西省大同市2022-2023学年八年级下学期期末教学质量抽样监测数学试卷(含解析),共15页。试卷主要包含了考试结束后,将答题卡交回等内容,欢迎下载使用。












