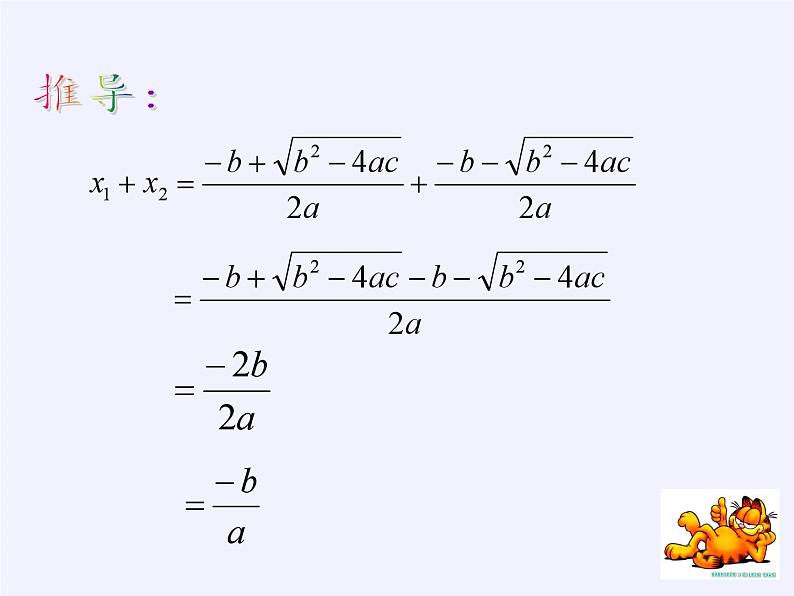
沪科版八年级下册17.4 一元二次方程的根与系数的关系教学课件ppt

这是一份沪科版八年级下册17.4 一元二次方程的根与系数的关系教学课件ppt，共30页。PPT课件主要包含了变式训练，感悟与反思，公式的特例，公式的应用，构造新方程，x2-5x+60，知识拓展等内容，欢迎下载使用。

1.一元二次方程的一般形式是什么？
3.一元二次方程的根的情况怎样确定？
2.一元二次方程的求根公式是什么？
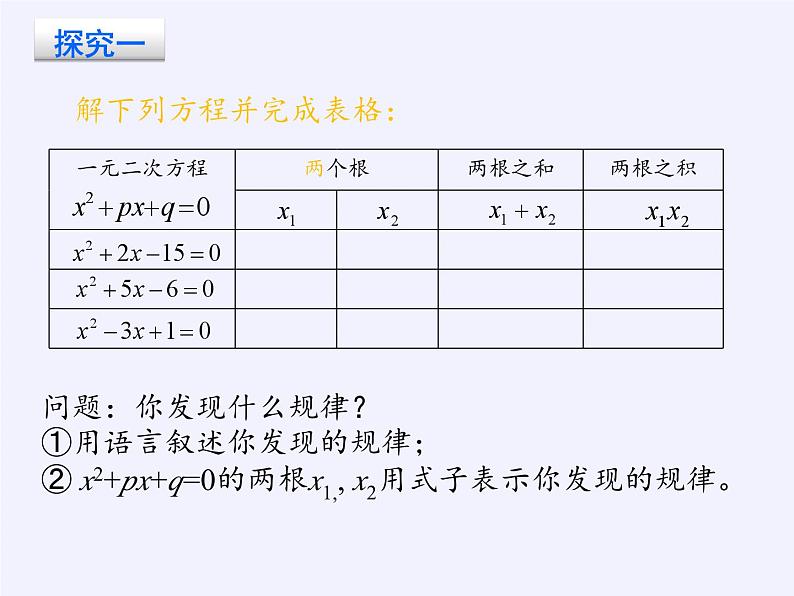
解下列方程并完成表格：
问题：你发现什么规律？①用语言叙述你发现的规律；② x2+px+q=0的两根x1,, x2用式子表示你发现的规律。
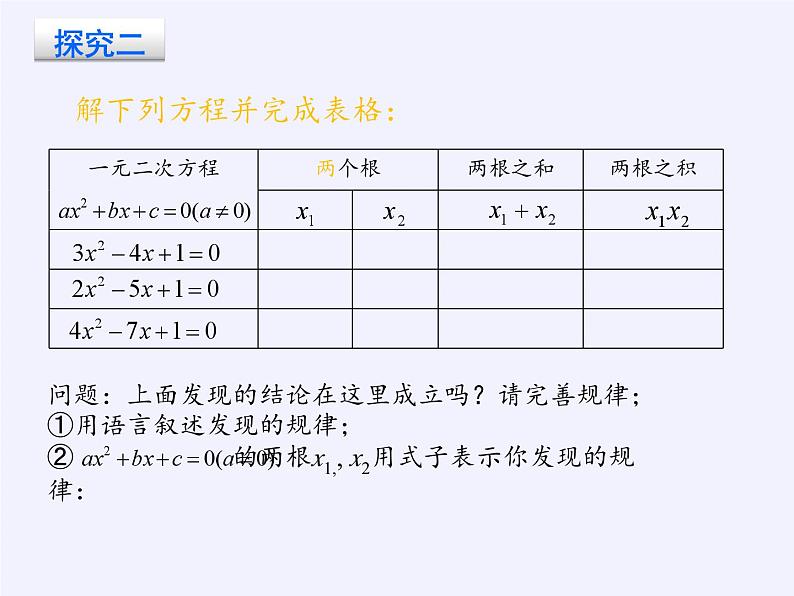
如果方程二次项系数不为1呢?
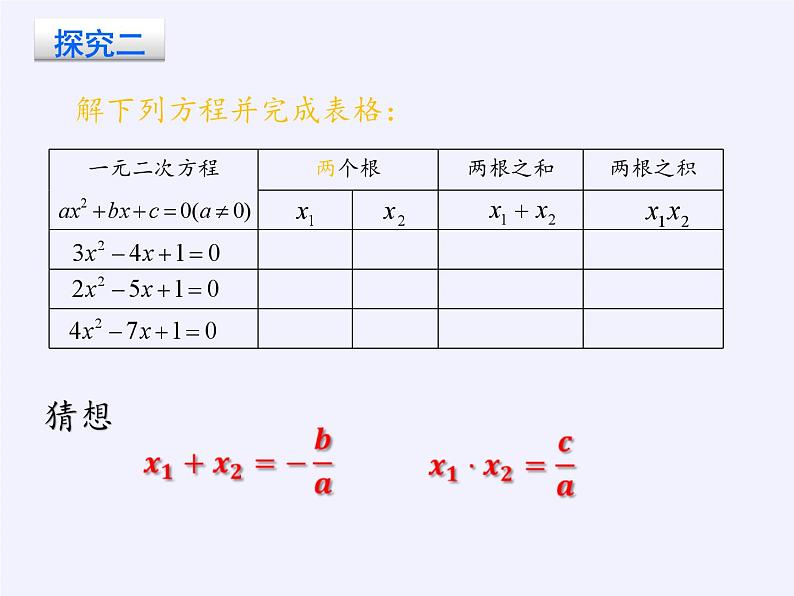
问题：上面发现的结论在这里成立吗？请完善规律；①用语言叙述发现的规律；② 的两根x1,, x2用式子表示你发现的规律：
这就是一元二次方程根与系数的关系，也叫韦达定理。
⑴要先化成一般形式，并找出a,b,c；
⑵确认a≠0，b2-4ac≥0；
(3)在使用 时，注意“－ ”不要漏写.
检验一元二次方程的解是否正确
利用根与系数的关系，判定下列各方程后面括号内的两个数是不是它的两个根?
利用根与系数的关系解决已知一根求 另一根的问题
利用根与系数的关系求与方程两根有关的代数式的值
设 是方程 的两个根，利用根与系数的关系，求下列各式的值.
关于两根几种常见的求值
已知关于方程两根的代数式的值，求方程中字母的系数
构造根满足某种条件的一元二次方程
已知方程 x2＋3x－2＝0，不解这个方程，利用根与系数的关系，求作一个一元二次方程，使它的根分别是已知方程的各根的 2 倍．
思路点拨：如果原方程的两个根为 x1，x2，则新方程的两个根为 2x1,2x2.则所求方程为 y2－(2x1＋2x2)y＋2x1·2x2＝0，只要求出 x1＋x2，x1x2 便可解出．
解：设原方程的两根为 x1，x2，则新方程的两个根为 2x1,2x2.又∵x1＋x2＝－3，x1·x2＝－2，∴2x1＋2x2＝－6,2x1·2x2＝－8.∴可设所求作的方程为
y2－(2x1＋2x2)y＋2x1·2x2＝0.即 y2＋6y－8＝0.
通过这节课的学习活动你有哪些收获？
在使用根与系数的关系时，应注意： ⑴要先化成一般形式，并找出a,b,c； ⑵确认a≠0，b2-4ac≥0；（3）在使用X1+X2=－ 时，注意“－ ”不要漏写.
2.应用一元二次方程的根与系数关系时，首先要把已知方程化成一般形式.
3.应用一元二次方程的根与系数关系时，要特别注意，方程有实根的条件，即在初中代数里，当且仅当 时，才能应用根与系数的关系.
1.一元二次方程根与系数的关系是什么?
一元二次方程根与系数的关系
甲、乙二人解同一个一元二次方程时，甲看错了常数项所求出的根为1，4；乙看错了一次项系数所求出的根是-2，-3。则这个一元二次方程为
跳水运动员要在空中下落的短暂过程中完成一系列高难度的动作，如果不考虑空气阻力等其他因素影响，弹跳到最高点后，人体下落到水面所需要的时间t与下落的高度h之间应遵循下面的公式：
其中h 的单位是 m，t 的单位是s，g=9.8 m/s2.假设跳板的高度是3 m，运动员在跳板上跳起1.2 m处开始下落，那么运动员下落到水面约需多长时间？