




初中数学沪科版八年级下册18.1 勾股定理课文ppt课件
展开相传2500年前,一次毕达哥拉斯去朋友家作客,发现朋友家用砖铺成的地面反映直角三角形三边的某种数量关系,同学们,我们也来观察下面的图案,看看你能发现什么?
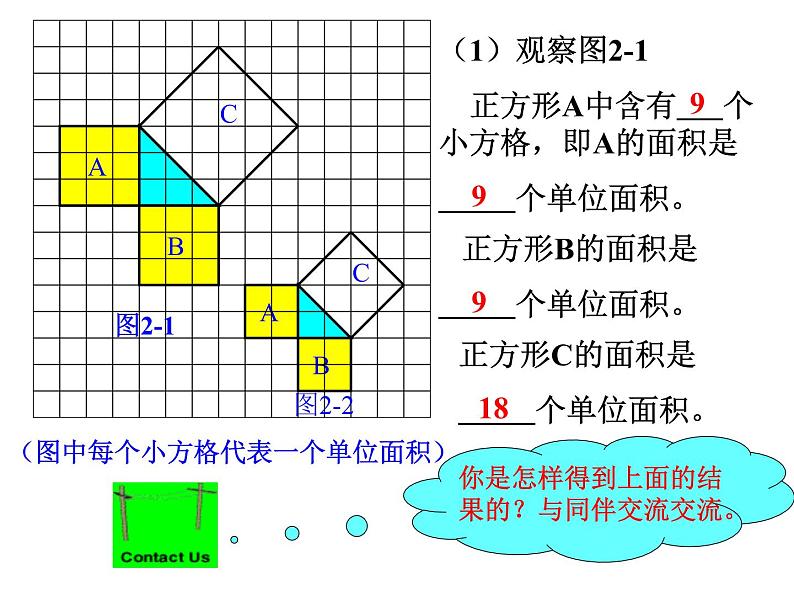
(1)观察图2-1 正方形A中含有 个小方格,即A的面积是 个单位面积。
正方形B的面积是 个单位面积。
正方形C的面积是 个单位面积。
分“割”成若干个直角边为整数的三角形
把C“补” 成边长为6的正方形面积的一半
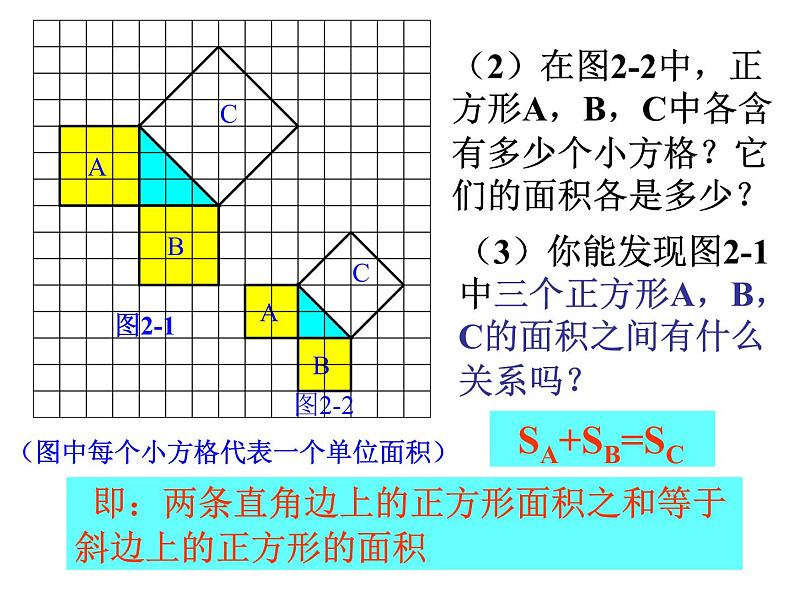
(2)在图2-2中,正方形A,B,C中各含有多少个小方格?它们的面积各是多少?
(3)你能发现图2-1中三个正方形A,B,C的面积之间有什么关系吗?
即:两条直角边上的正方形面积之和等于 斜边上的正方形的面积
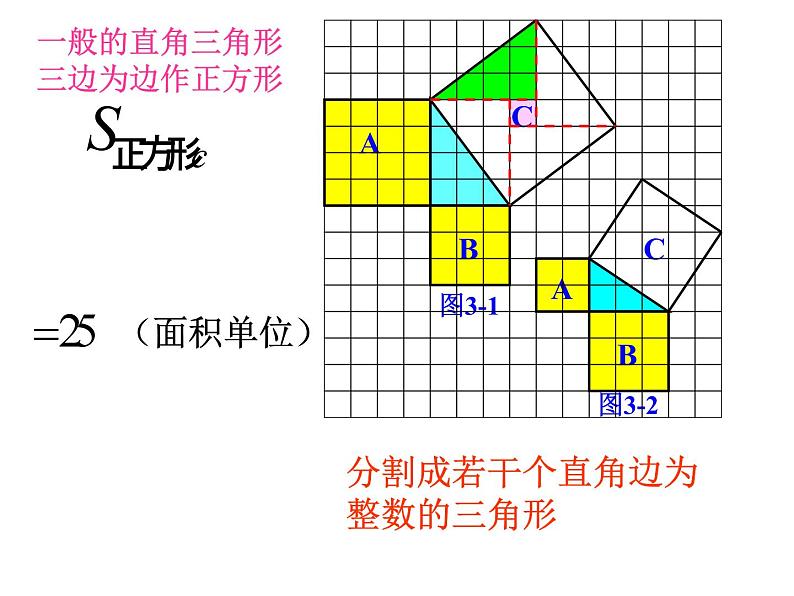
分割成若干个直角边为整数的三角形
一般的直角三角形三边为边作正方形
把C“补”成边长为7的正方形面积加1单位面积的一半
思考:面积A,B,C还有上述关系吗?
(1)你能用三角形的边长表示正方形的面积吗?
(2)你能发现直角三角形三边长度之间存在什么关系吗?与同伴进行交流。
观察所得到的各组数据,你有什么发现?
猜想:两直角边a、b与斜边c 之间的关系?
猜想两直角边a、b与斜边c 之间的关系?
直角三角形两直角边的平方和等于斜边的平方.
读一读 我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦.图1-1称为“弦图”,最早是由三国时期的数学家赵爽在为《周髀算经》作法时给出的.图1-2是在北京召开的2002年国际数学家大会(TCM-2002)的会标,其图案正是“弦图”,它标志着中国古代的数学成就.
两千多年前,古希腊有个哥拉
斯学派,他们首先发现了勾股定理,因此
在国外人们通常称勾股定理为毕达哥拉斯
年希腊曾经发行了一枚纪念票。
定理。为了纪念毕达哥拉斯学派,1955
国家之一。早在三千多年前,
国家之一。早在三千多年前
两千多年前,古希腊有个毕达哥拉斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理。为了纪念毕达哥拉斯学派,1955年希腊曾经发行了一枚纪念邮票。
我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中。
1.求下列图中表示边的未知数x、y、z的值.
P的面积 =______________
X=____________
AB=__________
AC=__________
BC=__________
2.求下列直角三角形中未知边的长:
可用勾股定理建立方程.
1、如图,一个高3 米,宽4 米的大门,需在相对角的顶点间加一个加固木条,则木条的长为 ( )
A.3 米 B.4 米 C.5米 D.6米
2、湖的两端有A、B两点,从与BA方向成直角的BC方向上的点C测得CA=130米,CB=120米,则AB为 ( )
A.50米 B.120米 C.100米 D.130米
1876年4月1日,伽菲尔德在《新英格兰教育日志》上发表了他对勾股定理的这一证法。1881年,伽菲尔德就任美国第20任总统。后来,人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就把这一证法称为“总统证法”。
对比两个图形,你能直接观察验证出勾股定理吗?
两幅图中彩色的四个直角三角形总面积呢?
提示:图中的两个大正方形面积相等吗?
空白部分的面积呢?那剩余的
如图,大风将一根木制旗杆吹裂,随时都可能倒下,十分危急。接警后“119”迅速赶到现场,并决定从断裂处将旗杆折断。现在需要划出一个安全警戒区域,那么你能确定这个安全区域的半径至少是多少米吗?
初中数学沪科版八年级下册18.1 勾股定理课文内容ppt课件: 这是一份初中数学沪科版八年级下册<a href="/sx/tb_c70391_t3/?tag_id=26" target="_blank">18.1 勾股定理课文内容ppt课件</a>,共19页。PPT课件主要包含了创设情境引入新课,探索新知,毕达哥拉斯,探究一,探究二,如何证明,猜一猜,a+b2,经典再现,拼一拼等内容,欢迎下载使用。
初中数学沪科版八年级下册第18章 勾股定理18.1 勾股定理教案配套课件ppt: 这是一份初中数学沪科版八年级下册<a href="/sx/tb_c70391_t3/?tag_id=26" target="_blank">第18章 勾股定理18.1 勾股定理教案配套课件ppt</a>,共14页。PPT课件主要包含了温故知新,直角三角形,两个锐角互余,继续思考,证明定理,当堂训练,成立条件,公式变形,在直角三角形中,“知二求一”等内容,欢迎下载使用。
沪科版18.1 勾股定理示范课ppt课件: 这是一份沪科版<a href="/sx/tb_c70391_t3/?tag_id=26" target="_blank">18.1 勾股定理示范课ppt课件</a>,共19页。PPT课件主要包含了第18章第1课时,一直角边2,另一直角边2,斜边2,a2+b2c2,∵S大正方形=c2,赵爽弦图,b-a,推荐书目,c2a2+b2等内容,欢迎下载使用。













