沪科版八年级下册第18章 勾股定理18.2 勾股定理的逆定理示范课课件ppt

这是一份沪科版八年级下册第18章 勾股定理18.2 勾股定理的逆定理示范课课件ppt，共14页。PPT课件主要包含了2两锐角互余，3勾股定理，问题引入，合作探究，动手画一画量一量，证明猜想，勾股定理，勾股定理的逆命题，互逆命题，a2+b2c2等内容，欢迎下载使用。

2.一个三角形满足什么条件是直角三角形？
①有一个内角是90°，那么这个三角形就是直角三角形;
②如果一个三角形中，有两个角的和是90°，那么这个三角形就是直角三角形.
1. 直角三角形有哪些性质？
(1)有一个角是直角；
(4)直角三角形30°角的性质.
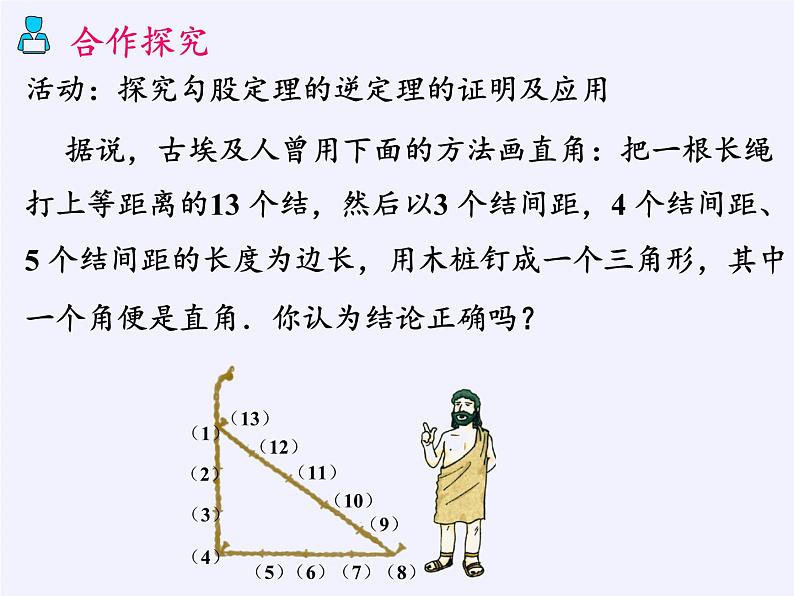
　据说，古埃及人曾用下面的方法画直角：把一根长绳打上等距离的13 个结，然后以3 个结间距，4 个结间距、5 个结间距的长度为边长，用木桩钉成一个三角形，其中一个角便是直角．你认为结论正确吗？
活动：探究勾股定理的逆定理的证明及应用
　　 实验操作： 分别以 6cm，8cm，10cm为边长画出三角形，所画出的图形是直角三角形吗？
（2）它们都是直角三角形吗？
（3）提出你的猜想：
猜想： 如果三角形的三边长a 、b 、c满足 a2+b2=c2 那么这个三角形是直角三角形.
由上面的例子你有什么发现？
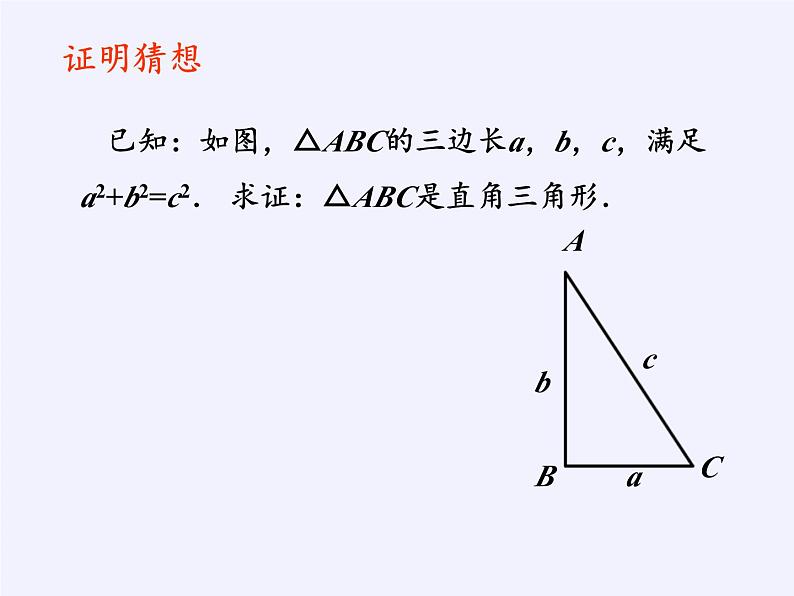
　已知：如图，△ABC的三边长a，b，c，满足a2+b2=c2． 求证：△ABC是直角三角形．
　已知：如图，△ABC的三边长a，b，c，满足a2+b2=c2． 　求证：△ABC是直角三角形．
证明：作Rt△A′B′C′，使∠C′=900，A′C′=b，B′C′=a
∴△ABC≌ △A′B′C′(SSS)
∴∠C= ∠C′=900 △ABC是直角三角形.
如果三角形的三边长a 、b 、c满足 a2+b2=c2那么这个三角形是直角三角形.
如果直角三角形的两直角边分别为a 、b ，斜边为c满足a2+b2=c2.
特别说明：勾股定理的逆定理是直角三角形的判定定理，即已知三角形的三边长，且满足两条较小边的平方和等于最长边的平方，即可判断此三角形为直角三角 ，最长边所对角为直角.
例1 下面以a,b,c为边长的三角形是不是直角三角形？如果是那么哪一个角是直角？
(1) a=25 b=20 c=15;
(2) a=13 b=14 c=15;
(4) a:b: c=3:4:5;
（1）3，4，5；（2）6，8，10；（3）5，12，13；（4）7，24，25；
像15，20，25这样，能成为直角三角形三条边长的正整数，称为勾股数.
一组勾股数，都扩大相同倍数k，得到一组新数，这组数同样是勾股数.
（1）勾股定理的逆定理的内容是什么？它有什么作用？
内容是：如果三角形的三边长a 、b 、c满足 a2+b2=c2那么这个三角形是直角三角形.作用：把数转化为形，通过计算三角形三边之间的关系来判断一个三角形是否是直角三角形，它可作为直角三角形的判定依据.