

2024年安徽省中考数学模拟卷一
展开1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答第Ⅰ卷时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。写在本试卷上无效。
3.回答第Ⅱ卷时,将答案写在答题卡上。写在本试卷上无效。
4.考试结束后,将本试卷和答题卡一并交回。
一、选择题(每小题4分,有10小题,共40分)
1.2023的倒数是()
A.2023B.-2023C.12023D.0
2.下列计算正确的是( )
A.3a2+a=4a3B.-2a-b=-2a+b
C.5a-4a=1D.a2b-2a2b=-a2b
3.今年是全民义务植树开展40周年.40年来,全民义务植树在中华大地蓬勃展开.截止12月13日,全国适龄公民累计17500000000人次参加义务植树,累计植树78100000000株(含折算),数据“17500000000”用科学记数法表示为( )
A.1.75×108B.17.5×108C.1.75×109D.1.75×1010
4.已知线段b是线段a、c的比例中项,如果a=4,c=9,那么线段b的长为( )
A.94B.6C.±6D.36
5.从1,2,3,4四个数中随机选取两个不同的数,分别记为a,c,则关于x的一元二次方程ax2+3x+c=0有实数根的概率为( )
A.23B.13C.14D.16
6.如图是由6个大小相同的正方体搭成的几何体,这个几何体的左视图是( )
A.B.C.D.
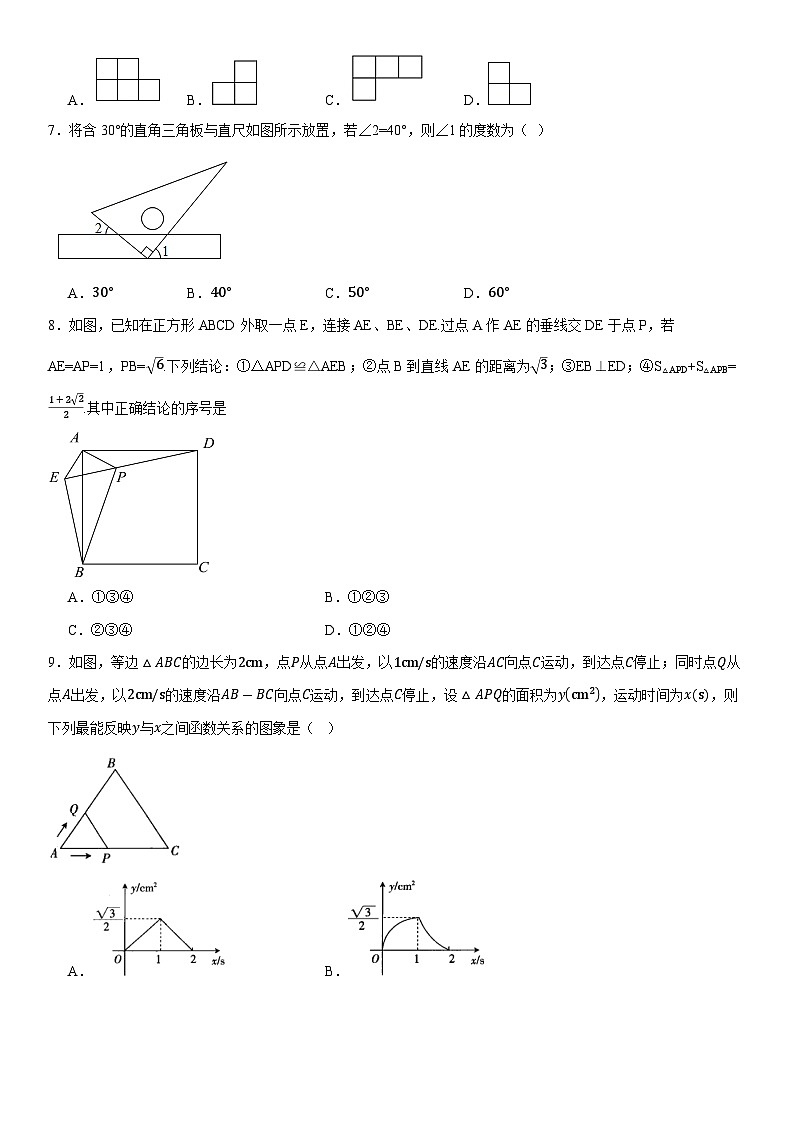
7.将含30°的直角三角板与直尺如图所示放置,若∠2=40°,则∠1的度数为( )
A.30°B.40°C.50°D.60°
8.如图,已知在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P,若AE=AP=1,PB=6.下列结论:①△APD≌△AEB;②点B到直线AE的距离为3;③EB⊥ED;④S△APD+S△APB=1+222.其中正确结论的序号是
A.①③④B.①②③
C.②③④D.①②④
9.如图,等边△ABC的边长为2cm,点P从点A出发,以1cm/s的速度沿AC向点C运动,到达点C停止;同时点Q从点A出发,以2cm/s的速度沿AB-BC向点C运动,到达点C停止,设△APQ的面积为ycm2,运动时间为xs,则下列最能反映y与x之间函数关系的图象是( )
A.B.
C.D.
10.如图,△ABC内接于⊙O,AC=BC=8,AD是⊙O的直径,连结BD,AE平分∠BAC交BD于E,若DE=2,则⊙O的半径为( )
A.92B.133C.174D.5
二、填空题(每小题5分,共4小题,共20分)
11.因式分解4m2-4mn-2m= .
12.关于x的一元二次方程x2+6x+m=0有两个实数根,则m的取值范围是 .
13.如图,在Rt△ABC中,∠ACB=90°,斜边AB=2,过点C作CF∥AB,以AB为边作菱形ABEF.若∠F=30°,∠EBC=15°,则Rt△ABC的面积为 .
14.如图,▱OABC的顶点B,C分别落在反比例函数y=ax(a>0,x>0)和y=bx(b<0,x<0)的图象上,连结OB,将△OBC沿着OB翻折,点C的对应点D恰好落在y=ax(a>0,x>0)的图象上,OD与BA交于点E.已知△OBE的面积为6,OE=3DE,则a-b的值为 ,ab的值为 .
三、解答题(共9小题,共90分)
15.计算:
(1)123--4-1×2+π-30
(2)a2⋅a3+-a43÷a7
16.我国古代数学著作《九章算术》中记载了这样一个问题:“今有五雀、六燕,集称之衡,雀俱重,燕俱轻,一雀一燕交而处,衡适平,并燕、雀重一斤,问燕、雀一枚各重几何?”其大意为:今有5只雀、6只燕,分别聚集而且用衡器称之,聚在一起的雀重,燕轻,将一只雀、一只燕交换位置而放,则衡器两边的总重量相等,如果5只雀和6只燕的总重量为一斤.问雀、燕每1只各重多少斤?
17.如图,在直角坐标系中,△ABC的三个顶点分别是A1,-4,B5,-4,C4,-1.
(1)将△ABC向上平移4格,画出平移后的△A1B1C1;
(2)将△ABC以点O为旋转中心顺时针旋转180°,画出旋转后对应的△A2B2C2;
(3)△A1B1C1与△A2B2C2关于点M成中心对称,则对称中心M的坐标是__________.
18.阅读材料,解答下列问题:
①两个含有二次根式的代数式相乘,如果它们的积不含有二次根式,我们就说这两个代数式互为有理化因式,例如:a与a,2+1与2-1.这样,化简一个分母含有二次根式的式子时,采用分子、分母同乘以分母的有理化因式的方法就可以了,例如:
将23+1化简:23+1=2(3-1)(3+1)(3-1)=2(3-1)(3)2-1=2(3-1)2=3-1,以上这种化简的步骤叫做分母有理化.
②学习数学,最重要的是学习数学思想,其中一种数学思想叫做换元的思想,它可以简化我们的计算.
(1)请你写出3+27的有理化因式: .
(2)计算:13+1+15+3+17+5+⋅⋅⋅+12019+2017.
(3)已知15+x2-26-x2=1,求15+x2+26-x2的值.
19.如图所示,无人机在生活中的使用越来越广泛,小明用无人机测量大楼的高度.无人机悬停在空中E处,测得楼AB楼顶A的俯角是60°,楼CD的楼顶C的俯角是45°,已知两楼间的距离BD=1003米,楼AB的高为10米,从楼AB的A处测得楼CD的C处的仰角是30°.(A、B、C、D、E在同一平面内).
(1)求楼CD的高;
(2)小明发现无人机电量不足,仅能维持60秒的飞行时间,为了避免无人机掉落砸伤人,站在A点的小明马上控制无人机从E处匀速以5米/秒的速度沿EA方向返航,无人机能安全返航吗?
20.如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,作DE⊥AC于点E.
(1)求证:DE与⊙O相切;
(2)若BD=2 5,AE=1,求⊙O的半径.
21.省射击队为从甲、乙两名运动员中选拔一人参加全国比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
(1)根据表格中的数据,计算出甲的平均成绩是 环,乙的平均成绩是 环;
(2)分别计算甲、乙六次测试成绩的方差;
(3)根据(1)、(2)计算的结果,你认为推荐谁参加全国比赛更合适,请说明理由.
计算方差的公式:s2=1n[(x1-x)2+(x2-x)2++(xn-x)2] .
22.已知:在矩形ABCD中,把矩形ABCD绕点C旋转,得到矩形FECG,且点E落在AD边上,连接BG交CE于点H.
(1)如图1,连接BE.
①求证:BE平分∠AEC;
②求证:H是BG的中点;
(2)如图2,连接FH,若FH平分∠EFG,CH=2,求AE的长.
23.如图1,抛物线y=ax2+b与x轴交于A、B两点,与y轴交于点C,点A的坐标是(2,0),点C的坐标是(0,4).
(1)求抛物线的解析式;
(2)如图2,点P是第四象限内抛物线上一点,连接PB交y轴于点E,设点P的横坐标为t,线段CE的长为d,求d与t之间的函数关系式,并直接写出自变量t的取值范围;
(3)如图3,点D是第三象限内抛物线上一点,连接PD交y轴于点F,过点D作DM⊥BP于点H,交x轴于点M,连接AD交BP于点N,连接MN,若EF=d2,∠BND=∠ANM时,求点P的坐标.
参考答案
1.【答案】C
2.【答案】D
3.【答案】D
4.【答案】B
5.【答案】D
6.【答案】D
7.【答案】C
8.【答案】A
9.【答案】D
10.【答案】B
11.【答案】2m2m-2n-1
12.【答案】m≤9
13.【答案】0.5 / 12
14.【答案】 16 -35/-0.6
15.【答案】(1)解:123--4-1×2+π-30
=18+14×2+1
=18+12+1
=138;
(2)解:a2⋅a3+-a43÷a7
=a5-a12÷a7
=a5-a5
=0.
16.【答案】解:设每只雀重x斤,每只燕重y斤,
根据题意,得5x+6y=14x+y=5y+x,
解得x=219y=338,
答:每只雀重219斤,每只燕重338斤.
17.(1)如图,△A1B1C1即为所求.
(2)如图,△A2B2C2即为所求.
(3)连接A1A2,B1B2,C1C2,相交于点M,
则△A1B1C1绕点M旋转180°能得到△A2B2C2
由图可得,A11,0,A2-1,4,
∴旋转中心点M的坐标为0,2.
故答案为:0,2.
18.【答案】(1)3-27
(2)解:原式=3-13-1+5-35-3+7-57-5+⋅⋅⋅+2019-20172019-2017
=3-1+5-3+7-5+⋅⋅⋅+2019-20172
=2019-12
(3)解:(15+x2-26-x2)2
=15+x2-215+x2·26-x2+26-x2
=41-215+x2·26-x2
则
215+x2·26-x2=40
(15+x2+26-x2)2
=15+x2+215+x2·26-x2+26-x2
=41+215+x2·26-x2
=81
∵15+x2≥0,26-x2≥0,
∴15+x2+26-x2=9.
19.【答案】(1)如图所示,
过点A做AF∥BD,交CD于点F,
∴∠AFC=∠BDC=90°,AF=BD=100 3m
在Rt△AFC中, ∵∠CAF=30°,
∴ CF=AFtan30°=1003×33=100m,AC=2CF=200m,
∴CD=CF+FD=100+10=110m,
答:楼CD高110m;
(2)依题意可知,∠AEC=180°-60°-45°=75°,∠EAF=60°,
∵∠CAF=30°,
∴∠EAC=∠EAF-∠CAF=60°-30°=30°,
在△EAC中,∠ECA=180°-∠EAC-∠AEC=180°-30°-75°=75°,
∴∠ECA=∠AEC,
∴AE=AC=200m,
无人机可飞行距离:s=vt=5×60=300m
∵300>200
∴ 无人机能安全返航
20.【答案】(1)证明:连接OD
∵AB为⊙O的直径,
∴AD⊥BC,
又∵AB=AC,
∴BD=CD,
又∵OA=OB,
∴OD为△ABC的中位线
∴OD∥AC,
又∵DE⊥AC,
∴DE⊥OD,
∴DE与⊙O相切;
(2)∵AD⊥BC,DE⊥AC,
∴∠CED=∠CDA=90°,
∵∠C=∠C,
∴ △CDE ∽ △CAD,
∴ CDCA=CECD,
∴CD2=CA×CE,
由(1)知:CD=BD=25 ,
即AC×AC-1=20,
解得AC=5或AC=-4 (舍),
∴⊙O的半径OD=12AB=12AC=2.5.
21.【答案】解:(1)(1)甲:(10+8+9+8+10+9)÷6=9(环),
乙:(10+7+10+10+9+8)÷6=9(环);
故答案为:9;9.
(2)s2甲=16×(10-9)2+(8-9)2+(9-9)2+(8-9)2+(10-9)2+(9-9)2
=16×(1+1+0+1+1+0)
=23;
s2乙=16×(10-9)2+(7-9)2+(10-9)2+(10-9)2+(9-9)2+(8-9)2
=16×(1+4+1+1+0+1)
=43.
(3)推荐甲参加全国比赛更合适,理由如下:两人的平均成绩相等,说明实力相当;但甲的六次测试成绩的方差比乙小,说明甲发挥较为稳定,故推荐甲参加比赛更合适.
22.【答案】(1)证明①如图,
由旋转性质得EC=BC,
∴∠CEB=∠CBE,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠AEB=∠CBE,
∴∠AEB=∠CEB,
∴BE平分∠AEC;
②如图,过点B作BP⊥CE于点P,
由①可知∠AEB=∠CEB,
又∵∠A=∠BPE,且BE=BE,
∴△AEB≌△PEB(AAS),
∴BP=BA,
∵BA=DC=GC,
∴BP=GC,
又∵∠BHP=∠GHC,∠BPH=∠GCH=90°,
∴△BPH≌△GCH(AAS),
∴BH=HG,
∴点H为BG中点,
(2)解:如图,作BP⊥CE于点P,
由(1)可知△AEB≌△PEB,△BPH≌△GCH,
∴AE=PE,PH=CH=2,
∵∠EFG=∠FEH=90°,FH平分∠EFG,
∴∠EFH=12∠EFG=45°
∴∠EHF=45°=∠EFH,
∴EF=EH=BA=DC,
设AE=PE=x,则EC=x+4,EH=x+2,
∴BC=EC=AD=x+4,EF=EH=BA=DC=x+2,
∴ED=AD-AE=4,
∵∠EDC=90°,
∴(x+2)2+42=(x+4)2,
解得x=1,
∴AE=1.
23.【答案】(1)解:0=4a+b4=b解得a=-1b=4,∴拋解:y2=-x2+4
(2)解:作OR⊥x轴于H,
∵P(t2,-t2+4),∴PR=t2-4,
∴解得0=-x2+4得x1=x2,∴B(-3,0),∴BR=t+2,BO=2,
∵tan∠ABP=OE/BO=PR/BR,∴OE/2=t2-4/t+2
∴OE=2t-4,∴d=CO+OE=4+2t-4=2t(t>2)
(3)解:作DG⊥x轴于G,PK⊥DG于K交y轴于L
设,D(n,4-n2)则PK=t-n,DK=(4-t2)-(4-n2)=(n-t)(n+t)
∵ED=d/2=t,∴OF=OE+EF=3t-4
∴LF=OF-OL=(3t-4)-(t2-4)=t(3-t)
∵tan∠KPD=LF/LP,∴n=-3,∴D(-3,-5)
∴AG=2-(-3)=5=DG,又∠DGA=90°,∴∠1=∠GDA=45°
作AQ垂直于x轴交BP于Q,则∠2=45°=∠1,第一次
第二次
第三次
第四次
第五次
第六次
甲
10
8
9
8
10
9
乙
10
7
10
10
9
8
2024年安徽省中考数学模拟预测卷(含答案): 这是一份2024年安徽省中考数学模拟预测卷(含答案),共17页。试卷主要包含了4×109D,0B,下列一元二次方程有实数根的是等内容,欢迎下载使用。
(冲刺中考)安徽省2024年中考数学模拟预测卷(二)(含解析): 这是一份(冲刺中考)安徽省2024年中考数学模拟预测卷(二)(含解析),共25页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
(冲刺中考)安徽省2024年中考数学模拟预测卷(含答案): 这是一份(冲刺中考)安徽省2024年中考数学模拟预测卷(含答案),共25页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。












