北京市通州区2023-2024学年八年级下学期期中数学试题（原卷版+解析版）

这是一份北京市通州区2023-2024学年八年级下学期期中数学试题（原卷版+解析版），文件包含北京市通州区2023-2024学年八年级下学期期中数学试题原卷版docx、北京市通州区2023-2024学年八年级下学期期中数学试题解析版docx等2份试卷配套教学资源，其中试卷共35页， 欢迎下载使用。
考生须知：
1．本试卷共8页，共三道大题，28个小题，满分为100分，考试时间为120分钟．
2．请在试卷和答题卡上准确填写学校名称、班级、姓名．
3．试题答案一律填涂或书写在答题卡上，在试卷上作答无效．
4．在答题卡上，选择题、作图题用2B铅笔作答，其他试题用黑色字迹签字笔作答．
5．考试结束后，请将答题卡交回．
一、选择题（本题共8个小题，每小题2分，共16分）每题均有四个选项，符合题意的选项只有一个．
1 已知点A的坐标为（），那么点A在（ ）
A. 第一象限B. 第二象限C. 第三象限D. 第四象限
【答案】B
【解析】
【详解】分析：根据点A（-2，3）横纵坐标的特点，即可确定点A所在象限．
详解：因为点A（-2，3）横坐标是正数，纵坐标也是正数，所以点A在平面直角坐标系的第二象限．
故选：B．
点睛：解决本题的关键是掌握好四个象限的点的坐标的特征：第一象限正正，第二象限负正，第三象限负负，第四象限正负．
2. 如图，在中，对角线与相交于点，如果，那么的长是（ ）
A. 4B. 5C. 6D. 无法确定
【答案】C
【解析】
【分析】本题考查了平行四边形的性质，根据平行四边形的对角线互相平分即可求解．
【详解】解：∵在中，对角线与相交于点， ，
∴，
故选：C．
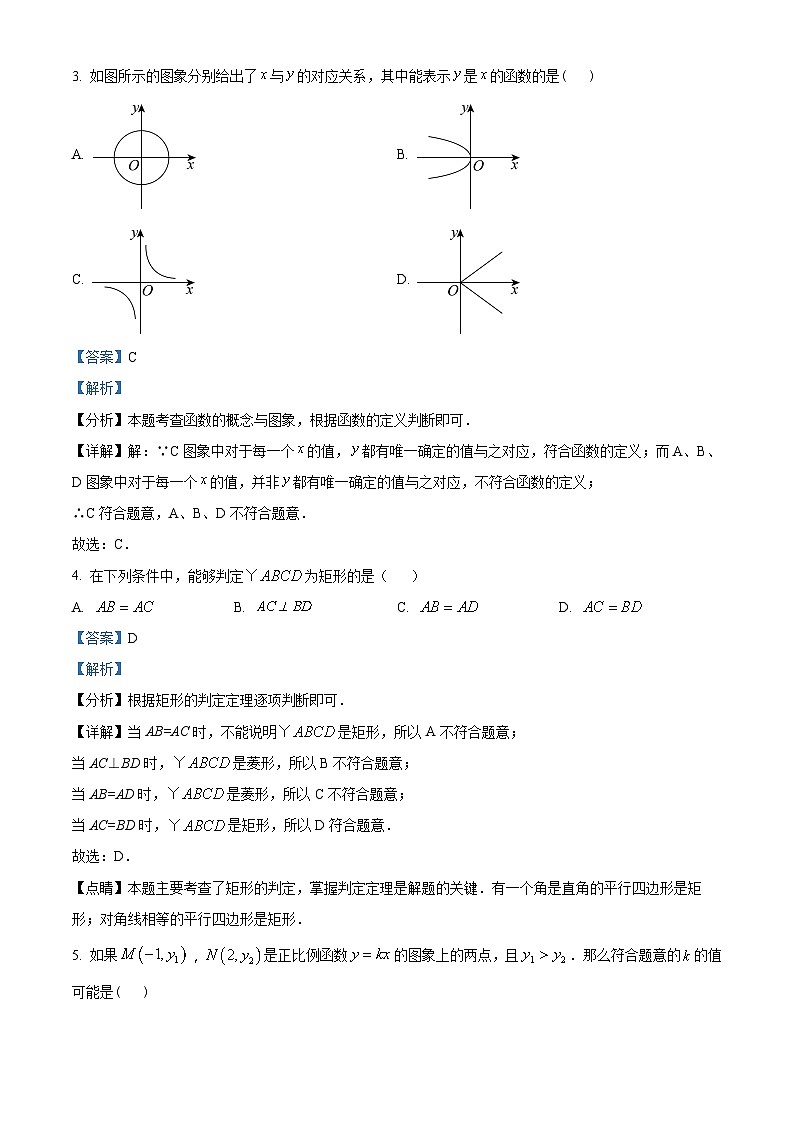
3. 如图所示的图象分别给出了与的对应关系，其中能表示是的函数的是( )
A. B.
C. D.
【答案】C
【解析】
【分析】本题考查函数的概念与图象，根据函数的定义判断即可．
【详解】解：∵C图象中对于每一个的值，都有唯一确定的值与之对应，符合函数的定义；而A、B、D图象中对于每一个的值，并非都有唯一确定的值与之对应，不符合函数的定义；
∴C符合题意，A、B、D不符合题意．
故选：C．
4. 在下列条件中，能够判定为矩形的是（ ）
A. B. C. D.
【答案】D
【解析】
【分析】根据矩形的判定定理逐项判断即可．
【详解】当AB=AC时，不能说明是矩形，所以A不符合题意；
当AC⊥BD时，是菱形，所以B不符合题意；
当AB=AD时，是菱形，所以C不符合题意；
当AC=BD时，是矩形，所以D符合题意．
故选：D．
【点睛】本题主要考查了矩形的判定，掌握判定定理是解题的关键．有一个角是直角的平行四边形是矩形；对角线相等的平行四边形是矩形．
5. 如果，是正比例函数的图象上的两点，且．那么符合题意的的值可能是( )
A. B. 1C. 3D.
【答案】D
【解析】
【分析】本题考查了正比例函数的性质，由时，，根据正比例函数的增减性，得到，即可得到答案．
【详解】解：∵，是正比例函数的图象上的两点，且．
∴，
故选：D．
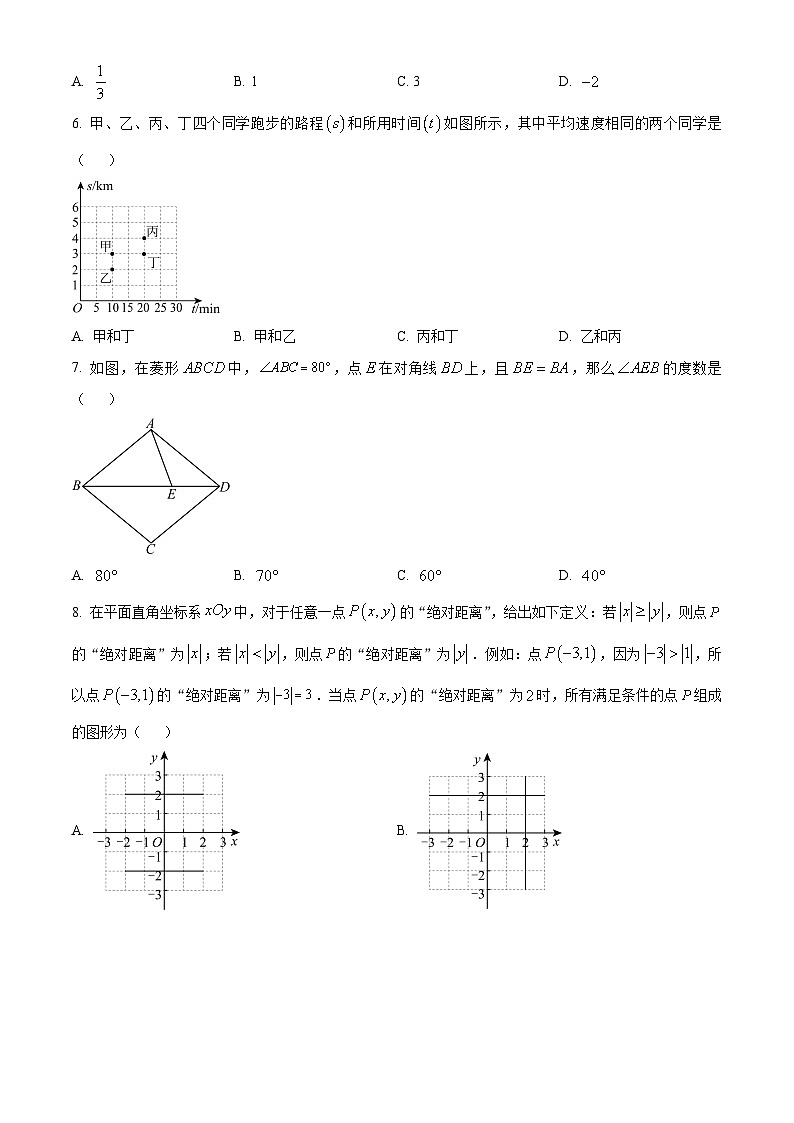
6. 甲、乙、丙、丁四个同学跑步的路程和所用时间如图所示，其中平均速度相同的两个同学是（ ）
A. 甲和丁B. 甲和乙C. 丙和丁D. 乙和丙
【答案】D
【解析】
【分析】本题考查了从图象中获取信息的能力，根据图中提供的数据分别求出甲、乙、丙、丁4个人的速度，再比较大小即可．
【详解】解：由图可知，
甲的速度为：，
乙的速度为：，
丙的速度为：，
丁的速度为，
其中平均速度相同的两个同学是乙和丙
故选：D．
7. 如图，在菱形中，，点在对角线上，且，那么的度数是（ ）
A. B. C. D.
【答案】B
【解析】
【分析】本题考查了菱形的性质，等边对等角以及三角形内角和定理，根据题意得出，根据已知条件得出，根据三角形内角和定理，即可求解．
【详解】解：∵在菱形中，，点在对角线上，
∴，
∵，
∴
故选：B．
8. 在平面直角坐标系中，对于任意一点的“绝对距离”，给出如下定义：若，则点的“绝对距离”为；若，则点的“绝对距离”为．例如：点，因为，所以点的“绝对距离”为．当点的“绝对距离”为时，所有满足条件的点组成的图形为（ ）
A. B.
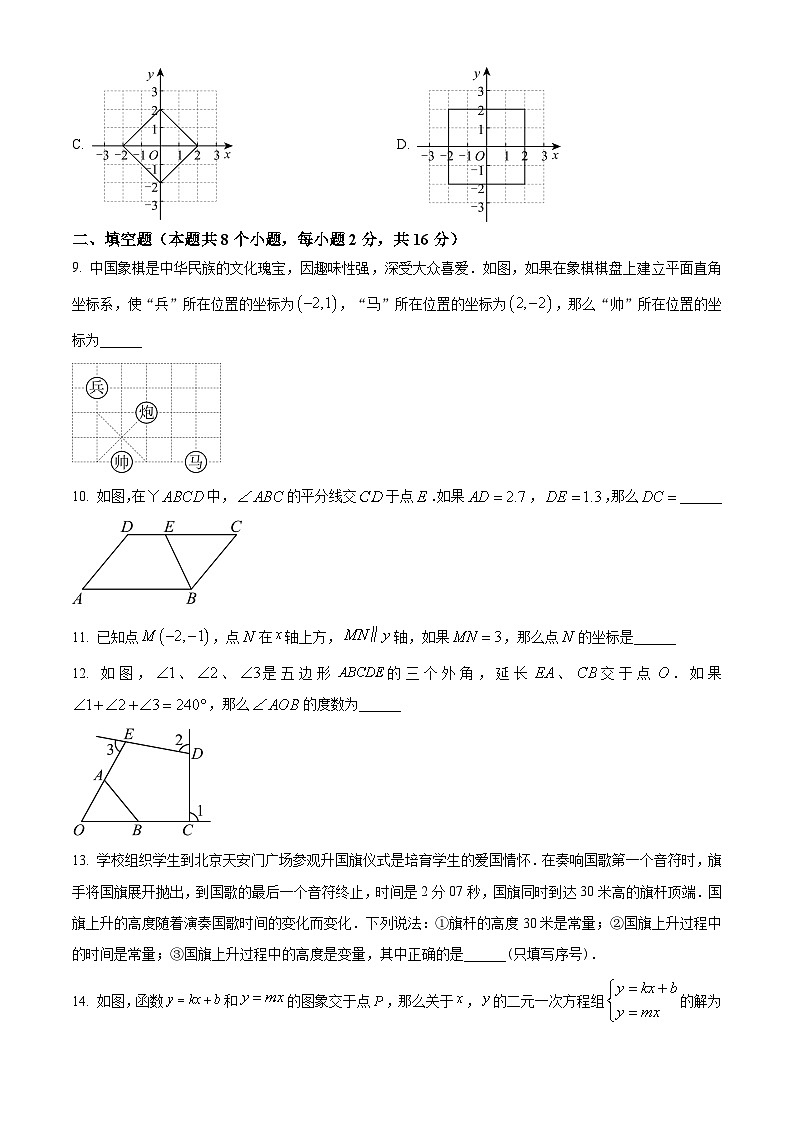
C. D.
【答案】D
【解析】
【分析】本题考查了坐标与图形，根据新定义分类讨论，结合新定义逐项分析判即可求解．
【详解】解：依题意，当时，，
当时，
∴当点的“绝对距离”为时，所有满足条件的点组成的图形为
故选：D．
二、填空题（本题共8个小题，每小题2分，共16分）
9. 中国象棋是中华民族的文化瑰宝，因趣味性强，深受大众喜爱．如图，如果在象棋棋盘上建立平面直角坐标系，使“兵”所在位置的坐标为，“马”所在位置的坐标为，那么“帅”所在位置的坐标为______
【答案】
【解析】
【分析】本题考查了直角坐标系的知识；根据直角坐标系的性质，结合“兵”位于点，“马”位于点，确定原点的位置和直角坐标系每小格的单位，从而得到“帅”的坐标．
【详解】解：如图所示，
“帅”所在位置的坐标为
故答案为：．
10. 如图，在中，的平分线交于点．如果，，那么______
【答案】
【解析】
【分析】本题考查了平行四边形的性质，角平分线的定义，等角对等边，根据平行四边形的性质与角平分线的定义可得，，，根据平行线的性质可得，进而可得，根据等角对等边可得，进而即可求解．
【详解】解：∵在中，的平分线交于点
∴，，
∴
∴
∴，
∵，
∴，
故答案为：．
11. 已知点，点在轴上方，轴，如果，那么点的坐标是______
【答案】
【解析】
【分析】本题考查坐标与图形性质，根据轴及点的坐标，可得出点的横坐标，再根据及点在轴上方，可确定点的纵坐标，进而可解决问题．
【详解】解：因为轴，且，
所以点的横坐标为．
因为，
所以，．
又因为点在轴上方，
所以点的坐标为．
故答案为：．
12. 如图，、、是五边形的三个外角，延长、交于点．如果，那么的度数为______
【答案】##度
【解析】
【分析】本题考查了多边形的外角，延长，根据多边形的外角和为得出，即可求解．
【详解】解：如图所示，
∵，
∴，
∴，
故答案为：．
13. 学校组织学生到北京天安门广场参观升国旗仪式是培育学生的爱国情怀．在奏响国歌第一个音符时，旗手将国旗展开抛出，到国歌的最后一个音符终止，时间是2分07秒，国旗同时到达30米高的旗杆顶端．国旗上升的高度随着演奏国歌时间的变化而变化．下列说法：①旗杆的高度30米是常量；②国旗上升过程中的时间是常量；③国旗上升过程中的高度是变量，其中正确的是______(只填写序号)．
【答案】①③##③①
【解析】
【分析】本题考查了函数的定义；根据常量与变量的定义判断即可．
【详解】解：旗杆的高度30米始终保持不变，是常量；而国旗上升过程中的时间一直在变化，是变量；国旗上升过程中的高度随时间而改变，是变量，
∴①③正确，②不正确．
故答案为：①③．
14. 如图，函数和的图象交于点，那么关于，的二元一次方程组的解为______
【答案】
【解析】
【分析】本题考查了一次函数与二元一次方程组的关系，根据方程组的解就是交点坐标写出即可．
【详解】解：∵函数和的图象交于点，，
∴关于，的二元一次方程组的解为，
故答案为：．
15. 如图，在四边形中，，对角线，交于点，现有三个条件①；②；③．其中可以判定四边形是平行四边形的有______(只写序号即可)．
【答案】①②##②①
【解析】
【分析】本题考查了平行四边形的判定以及全等三角形的判定与性质；根据平行四边形的判定方法分别对各个条件进行判断即可．
【详解】解：①，，
四边形是平行四边形，故①符合题意；
②，
，
又，，
，
，
四边形是平行四边形，故②符合题意；
③由，，不能判定四边形是平行四边形，故③不符合题意；
故答案为：①②．
16. 已知：如图，正方形中，是对角线的交点，过作分别交、于E、F，若，则_______
【答案】
【解析】
【详解】试题分析：先根据正方形的性质及证得△AEO≌△BFO，得出AE=BF，则BE=CF，再根据勾股定理即可求得结果．
,∵四边形ABCD是正方形
∴OA=OB，∠EAO=∠FBO=45°
又∵∠AOE+∠EOB=90°，∠BOF+∠EOB=90°
∴∠AOE=∠BOF，
∴△AEO≌△BFO
∴AE=BF=4
∴BE=CF=3，
考点：本题考查的是正方形的性质，全等三角形的判定和性质，勾股定理
点评：解答本题的关键是根据正方形的性质及证得△AEO≌△BFO.
三、解答题（本题共68分，第17-24题每小题5分，第25.26题每小题6分，第27，28题每小题8分）解答应写出文字说明、演算步骤或证明过程．
17. 已知函数．
（1）如果点在该函数的图象上，求的值；
（2）求出这个函数的图象与轴，轴的交点坐标．
【答案】（1）
（2）这个函数的图象与轴的交点为，与轴的交点为
【解析】
【分析】本题考查了一次函数的性质，求一次函数图象与坐标轴的交点．
（1）将点代入，即可求解．
（2）将，代入，求出的值，即得出这个函数的图象与轴的交点；将，代入，求出的值，即得出这个函数的图象与轴的交点，即可求解．
【小问1详解】
解：将代入，得，
，
解得：；
【小问2详解】
当时，，
这个函数的图象与轴的交点为；
当时，即，
解得：
这个函数的图象与轴的交点为．
18. 已知一次函数的图象过点，．
（1）求这个一次函数的表达式；
（2）在平面直角坐标系中，画出这个函数的图象．
【答案】（1）
（2）见解析
【解析】
【分析】本题考查了求一次函数解析式，画一次函数图象；
（1）待定系数法求解析式，即可求解．
（2）根据，直接画出函数图象，即可求解．
【小问1详解】
解：将，代入，得
解得：
【小问2详解】
解：过，画出函数图象，
如图所示
19. 如图，在中，点，分別在，上，连接，，与对角线分别交于点，．如果．求证：四边形是平行四边形．
【答案】见解析
【解析】
【分析】根据对顶角相等和已知条件得出，即可证明，进而根据四边形是平行四边形，得出，根据两组对边分别平行，即可得证．
【详解】证明：∵，，
∴，
∴
∵四边形是平行四边形，
∴
∴
∴四边形是平行四边形．
20. 已知函数的图象为，函数的图象为．
（1）在同一个直角坐标系中画出这两个函数的图象（不要求列表计算）；
（2）一次函数的图象为，请在坐标系中画出，，不能围成三角形的情形，并直接写出相对应的的值．
【答案】（1）见解析 （2）或或
【解析】
【分析】本题考查了两条直线相交或平行问题，画一次函数图象；
（1）先求得两直线与坐标轴的交点，进而画出函数图象，即可求解；
（2）当与或平行，，当经过和的交点坐标时，不能组成三角形．
【小问1详解】
解：对于，当时，，当时，，
对于，当时，，当时，，
过点画出，过点画出，如图所示
【小问2详解】
解：联立
解得：
当经过和的交点坐标时，不能组成三角形，则
解得：
∵当与或平行，或
∴的值为或或．
21. 如图，在矩形的边上取一点，使．过点作，垂足为点．如果，．求的长．
【答案】
【解析】
【分析】本题考查了矩形的性质，全等三角形的判定与性质，勾股定理等知识点，先证明然后证明，根据全等三角形的性质可得，进而勾股定理，即可求解．
【详解】解：由题意得：，
∴，
∴，
∵，
∴，
∴，
∴
22. 已知函数图象是由函数的图象平移得到，且经过点．
（1）求，的值；
（2）过点作轴的垂线交函数的图象于点，交函数的图象于点，过点作轴的平行线交的图象于点，请判断线段，的数量关系，并说明理由．
【答案】（1），
（2）
【解析】
【分析】本题考查了一次函数的平移，坐标与图形，求一次函数解析式，求函数值；
（1）根据平移可得，将代入得出；
（2）根据题意求得坐标，进而得．
【小问1详解】
解：∵函数的图象是由函数的图象平移得到，
∴
∵经过点．
∴；
【小问2详解】
解：由（1）可得的解析式为，
当时，，即，
∵轴，且在上，
∴，则
∵轴，且在上，
∴，则
∴．
23. 如图，在四边形中．，，对角线，交于点，平分．
（1）求证：四边形是菱形；
（2）点是边上动点(不与，重合)，过点作，，垂足分别为，，连接、．求证：．
【答案】（1）见解析 （2）见解析
【解析】
【分析】本题考查了菱形的判定与性质、矩形的判定、平行四边形的判定与性质、等腰三角形的判定；
（1）先证四边形是平行四边形，再证，则，然后由菱形的判定即可得出结论；
（2）由菱形的性质得则，再由，，得，然后证四边形是矩形，即可得出结论．
【小问1详解】
证明：，，
四边形是平行四边形，，
平分．
，
，
，
平行四边形是菱形．
【小问2详解】
由（1）可知，四边形是菱形，
，
，
，，
，
四边形是矩形，
．
24. 在平面直角坐标系中，一次函数（）的图象经过点和，与过点且平行于轴的直线交于点．
（1）求该函数的表达式及点的坐标；
（2）当时，对于的每一个值，一次函数的值都大于一次函数（）值，请直接写出的取值范围．
【答案】（1），
（2）
【解析】
【分析】本题考查了待定系数法求一次函数解析式，两直线交点问题；
（1）将点和，代入，待定系数法求解析式，令求得点的坐标；
（2）先求得当经过时，，结合函数图象，即可求解．
【小问1详解】
解：将点和，代入
∴
解得：
∴
∵过点且平行于轴的直线交于点．
当时，，解得：，
∴
【小问2详解】
解：如图所示，
当时，
当经过时，
∵当时，对于的每一个值，一次函数的值都大于一次函数（）值，
根据函数图象可得：．
25. 如图，在菱形中，对角线，交于点，过点作于点，延长到点，使，连接．
（1）求证：四边形是矩形；
（2）连接，若，，求长度．
【答案】（1）见解析 （2）
【解析】
【分析】（1）根据菱形的性质得到且，等量代换得到，推出四边形是平行四边形，根据矩形的判定定理即可得到结论；
（2）由菱形的性质得，由勾股定理求出，，再由直角三角形斜边上的中线性质即可得出答案．
【小问1详解】
证明：四边形是菱形，
且，
，
，
，
，
四边形是平行四边形，
，
，
四边形是矩形；
【小问2详解】
解：四边形是菱形，，
，
，
∴，
在中，，
在中，，
四边形是菱形，
，
．
【点睛】本题考查了矩形的判定和性质，菱形的性质，勾股定理，直角三角形斜边上的中线性质等；熟练掌握以上知识是解题的关键．
26. 某容器由上、下两个高度相同的圆柱体组合而成（如图），已知这个容器的高为，现向容器匀速注水，直至容器恰好注满时停止，每记录一次水面的高度（单位：），测了12次数据如下表所示：
（1）在平面直角坐标系中，描出上表中以各对对应值为坐标的点；根据描出的点，画出该函数的图象；
（2）在上面的圆柱体中，求水面高度与注水时间的函数关系式，并写出注水时间的取值范围；
（3）直接用等式表示上面圆柱体底面圆的半径与下面圆柱体底面圆的半径的关系．
【答案】（1）见解析 （2）
（3）
【解析】
【分析】本题考查了一次函数的应用；圆柱体的体积公式；
（1）根据表格数据，描点连续，即可求解；
（2）待定系数法求得第二段函数图象的解析式，即可求解；
（3）求得第一段函数解析式，得出下面圆柱体注水的速度是上面圆柱体注水的速度的，进而得出，即可求解．
【小问1详解】
解：如图所示，
【小问2详解】
解：将代入
∴
解得：
∴
∵这个容器的高为，现向容器匀速注水，直至容器恰好注满时停止，
∴当时，，解得：
∴
【小问3详解】
将，代入
∴
解得：
∴
∵，分别表示上面和下面的圆柱体的水面高度与时间的关系，
又
即下面圆柱体注水的速度是上面圆柱体注水的速度的倍，
∴
即
即
27. 如图，在正方形中，点是边上的一动点（不与点、重合），点关于直线的对称点为，连接，过点作交于点，交对角线于点．
（1）依据题意补全图形；
（2）如果，求的大小（用含的式子表示）；
（3）用等式表示线段与之间的数量关系，并证明．
【答案】（1）见解析 （2）
（3），证明见解析
【解析】
【分析】（1）根据题意补全图形，即可求解；
（2）根据轴对称得出，进而根据正方形的性质可得， 得出，进而根据三角形的外角的性质即可求解；
（3）过点作于点，则，根据（2）的结论得出，则，进而证明，得出，根据是等腰直角三角形，得出，根据轴对称的性质可得，即可求解．
【小问1详解】
解：如图所示，
【小问2详解】
解：∵点关于直线的对称点为，
∴，
∵四边形是正方形，是对角线，
∴，
∴，
∴，
∵
∴
∴；
【小问3详解】
解：如图所示，过点作于点，则
由（1）可得，
∴，
∴，
又∵，
∴，
∴，
∵，
∴是等腰直角三角形，
∴，
∵点关于直线的对称点为，
∴，
∴．
【点睛】本题考查了正方形的性质，等腰三角形的性质与判定，三角形的内角和定理与外角的性质，勾股定理，全等三角形的性质与判定，熟练掌握以上知识是解题的关键．
28. 对于平面直角坐标系中的图形和图形，给出如下定义：，分别为图形和图形上任意一点，将，两点间距离的最小值称为图形和图形之间的“关联距离”，记作．例如，如图①，点与轴之间的“关联距离”．
（1）如图②，已知点和点，则______；
（2）如图③，已知点，，，点是轴正半轴上一点，若，求点的坐标；
（3）已知，，当时，对于每一个的值，若线段和一次函数（是常数，）的图像之间的“关联距离”，请直接写出的取值范围．
【答案】（1）
（2）或或
（3）且．
【解析】
【分析】（1）根据“关联距离”的定义得：，勾股定理即可求解；
（2）分三种情况画出图形：当在上方时，的坐标是；当在线段上时，过作，可得；当在上方时，；
（3）求出直线过定点，当时，，，当时，，，直线过，时，分别求得的值，进而根据新定义，得出直线与平行四边形无公共点，结合图形，即可求解．
【小问1详解】
解：根据题意，，
故答案为：．
【小问2详解】
解：如图所示，点是轴正半轴上一点，
当在点上方时，，即点到点的距离为，
∴，
当在上方时，即点到的距离为，
∴，
∵点，，，
∴，
∴，是等腰直角三角形， 则平分，则到的距离相等，
过点作，则是等腰直角三角形，
∵，此时点到的距离为，即，
∴，
∴，
综上所述，或或；
【小问3详解】
解：如图所示，
当时，，
直线过定点，
当时，，，
当时，，，
把代入得：，
解得，
把代入得：，
解得，
线段和一次函数（是常数，）的图像之间的“关联距离”，
∴直线与平行四边形无公共点，
由图可知，此时．
∵
∴且
故答案为：且．
【点睛】本题考查一次函数的综合应用，涉及新定义，等腰直角三角形，平行四边形，勾股定理，解题的关键是分类讨论思想和数形结合思想的应用．注水时间
水面高度