北师大版（2021）拓展模块一 上册6.4.2 二面角示范课ppt课件

这是一份北师大版（2021）拓展模块一 上册6.4.2 二面角示范课ppt课件，共35页。PPT课件主要包含了∠AOB的特点，角的顶点在棱上，角的两边都与棱垂直，答案600，答案1200等内容，欢迎下载使用。
中职数学拓展模块一第六单元 立体几何
①使学生正确理解二面角与平面角的概念，并能初步运用它们解决问题；②进一步培养学生把空间问题转化为平面问题的化归思想。
①通过引导学生发现二面角的平面角的定义，培养学生的类比能力、观察能力、和归纳总结能力；②通过指导学生探求二面角的平面角的做法，培养学生自主探索能力与协作探究能力。
3.情感、态度与价值观
通过本节学习和运用实践，激发学生的学习积极性，培养思维的变通性和严密性，培养学生的探索精神和创新精神。
§6.4.2 二 面 角(2)
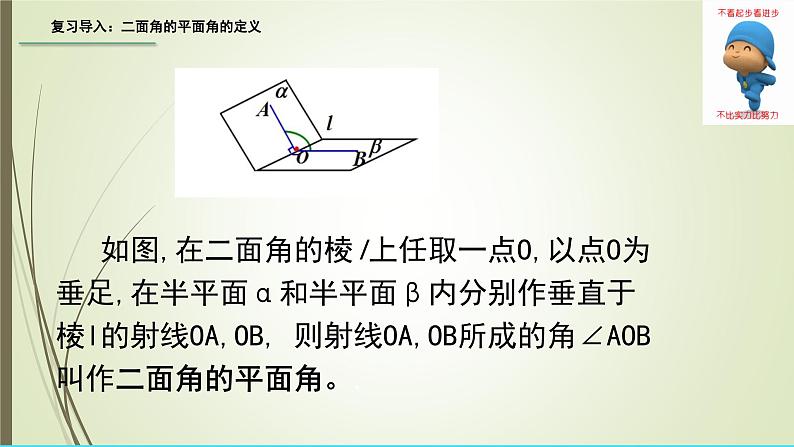
复习导入：二面角的平面角的定义
如图,在二面角的棱l上任取一点O,以点O为垂足,在半平面α和半平面β内分别作垂直于棱l的射线OA,OB, 则射线OA,OB所成的角∠AOB叫作二面角的平面角。.
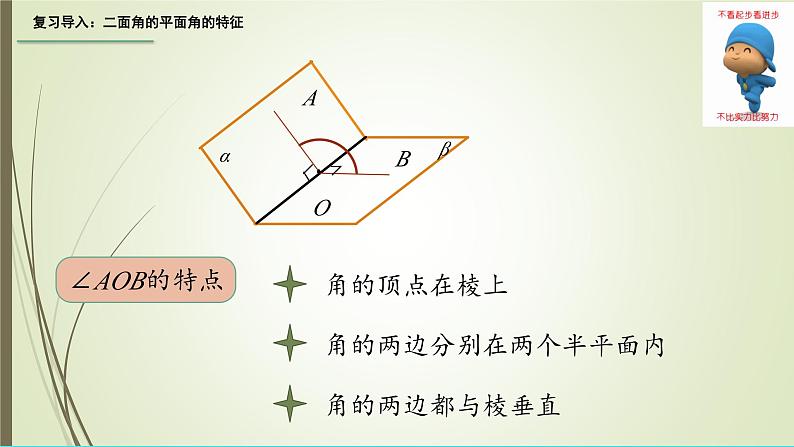
复习导入：二面角的平面角的特征
角的两边分别在两个半平面内
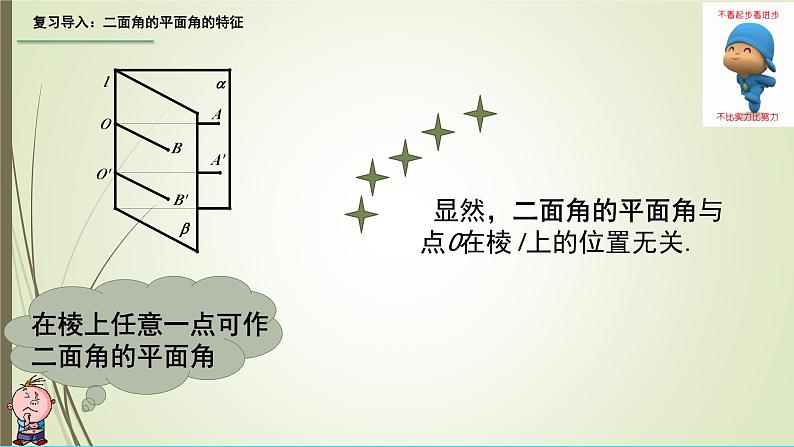
显然，二面角的平面角与点O在棱l上的位置无关.
复习导入：二面角的范围
当两个平面相交所成的四个二面角中，不大于直角的二面角称为两个平面的夹角.
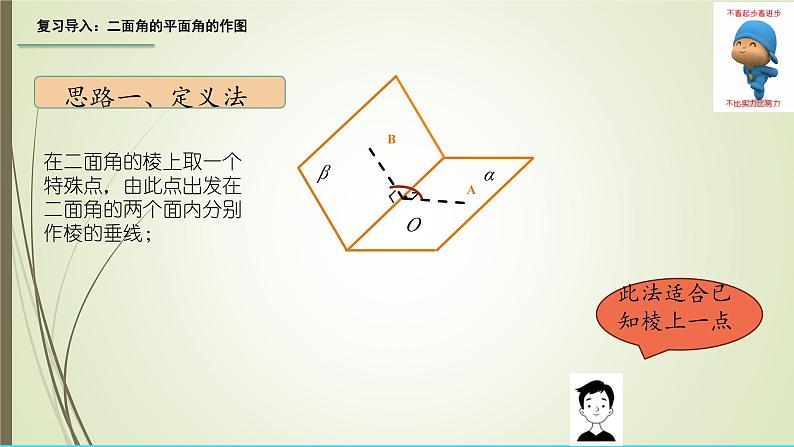
复习导入：二面角的平面角的作图
在二面角的棱上取一个特殊点，由此点出发在二面角的两个面内分别作棱的垂线；
如图，C是二面角β的面内的一个点，CO⊥α于O，只需作OD⊥AB，垂足为D，连接CD，用三垂线定理可证明∠CDO就是所求二面角的平面角
即在二面角的棱上取一点，过此点作平面，使垂直于二面角的棱，则 所作面与二面角的两个面的交线所成的角就是该二面角的平面角
应用二面角解决数学问题
例1、如图6-55 , 已知二面角α-l-β 的平面角为30°, 平面β内有一点P , 它到平面α的距离是2 , 求点P到棱l的距离.
【分析】过点P构造一个二面角的平面角,然后根据二面角的大小去求点P到棱l的距离.
解: 在平面β内, 过点P作PB⊥l交于点B , 再过点P作PA ⊥α, 垂足 为A , 连接AB , 则PA⊥l .
又∵ PB⊥l , PA∩PB = P , ∴ l⊥平面 PAB , ∴AB⊥l .
又∵ AB⊂α, PB ⊂β, ∴ ∠PBA为二面角的平面角.
∵在 Rt△PAB中, ∠PBA =30°, PA =2 , ∴PB =4 ,
∴点P到棱l的距离为4.
1. 已知在 的二面角的棱上有两个点M,N，线段MP,QN分别在这个二面角的两个面内 ,且都垂直于棱MN,若 ， ， ， 求PQ的值。
2. 山坡的倾斜度（坡面与水平面所成二面角的度数）是600，山坡上有一条直道CD，它和坡脚的水平线AB的夹角是300，沿这条路上山，行走100米后升高了多少米？
例1、如图6-56 , 在三棱锥 P-ABC 中, PA⊥平面 ABC , AB⊥AC , AB=AC=4 , PA =3 , 求二面角P-BC-A 的余弦值.
【分析】要求二面角的大小,也就是在棱BC上找一点,然后过这个点分别在两个半平面内作垂直于BC的射线,这两条射线所成的角就是所求二面角的平面角.
探究如何求二面角的大小
解 ： 取BC的中点E , 连接PE , AE .
∵PA⊥平面 ABC , 所以PA⊥AB , PA⊥AC , PA⊥ AE .
又∵AB = AC =4 , PA =3 , ∴PB = PC =5.
又∵E是BC的中点, ∴PE⊥BC , AE⊥BC .
又∵PE ⊂平面PBC , AE⊂平面ABC，∴∠ PEA 为二面角P-BC-A的平面角.
∵AB⊥AC , AB = AC =4 , ∴BC =42 , AE =22 , ∴PE = =17.
例2、已知P为二面角 内一点，且P到两个半平面的距离都等于P到棱的距离的一半，则这个二面角的度数是多少？
例3、如图，在四棱锥 中，底面 正方形，平面 平面 ， 为棱 的中点， ， ． (1)求证： 平面 ；(2)求二面角 平面角的大小.
归纳几何法如何求二面角的大小：
求二面角大小的基本步骤为：（1）找出或作出二面角的平面角；（2）证明其符合定义(垂直于棱)；（3）计算(解三角形)； （4）验证，作答(规范性) .
1.如图,在四面体P-ABC中,PC⊥平面ABC,AB＝BC＝AC＝PC,求二面角B－AP－C的正切值.
2. A为二面角α– CD –β的棱CD上一点，AB在平面α内且与棱CD成45º角，又AB与平面β成30º，求二面角α– CD – β的大小。
4. 已知在二面角的棱上有两个点A,B，线段AC,BD分别在这个二面角的两个面内 ,且都垂直于棱AB,若 ， ， ， ，求这个二面角的大小。
5. 已知如图，过二面角 内一点P分别作PA,PB垂直于 ， ， 求这个二面角的大小。
1.如图，AC⊥平面BCD，BD⊥CD， ，求平面ABD与平面BCD所成的二面角的大小.
2. 如图，已知AB垂直面ACD，DE垂直面ACD，ACD为等边三角形，AD=DE=2AB，F为CD的中点，（Ⅰ）求证：AF // 面BCE；（Ⅱ）求二面角A-CE-D的正切值.
1.AB⊥AC, PA⊥AC, 侧面PAC⊥底面ABC, PA=8, AB=AC=6 ①求二面角P - BC - A的正切值； ②求二面角A- PC- B的正切值
面PAC⊥底面ABC于AC
∴∠PEA为P- BC- A的平面角
侧面PAC⊥底面ABC于AC
∴∠AFB为A- PC- B的平面角
PA·AC=PC·AF,