2024年江苏省盐城市滨海县第一初级中学九年级中考数学模拟试卷

这是一份2024年江苏省盐城市滨海县第一初级中学九年级中考数学模拟试卷，共8页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1．温度从﹣2℃上升3℃后是（ ）
A．1℃B．﹣1℃C．3℃D．5℃
2．在现实世界中，对称现象无处不在，有些方块字也具有对称性．下列汉字是轴对称图形的是（ ）
A．B．C．D．
3．下列计算正确的是（ ）
A．a2+a3＝a5B．a2•a3＝a6C．（a2）3＝a6D．（ab）2＝ab2
4．如图是由一个长方体和一个圆柱组成的几何体，它的俯视图是（ ）
A．B．C．D．
5．若一正方形的面积为20，边长为x，则x的值介于下列哪两个整数之间（ ）
A．2，3B．3，4C．4，5D．5，6
6．如图是路政工程车的工作示意图，工作篮底部与支撑平台平行．若∠1＝30°，∠2＝50°，则∠3的度数为（ ）
A．130°B．140°C．150°D．160°
7．已知有理数x，y满足方程组，则2x+y的值为（ ）
A．﹣1B．0C．1D．2
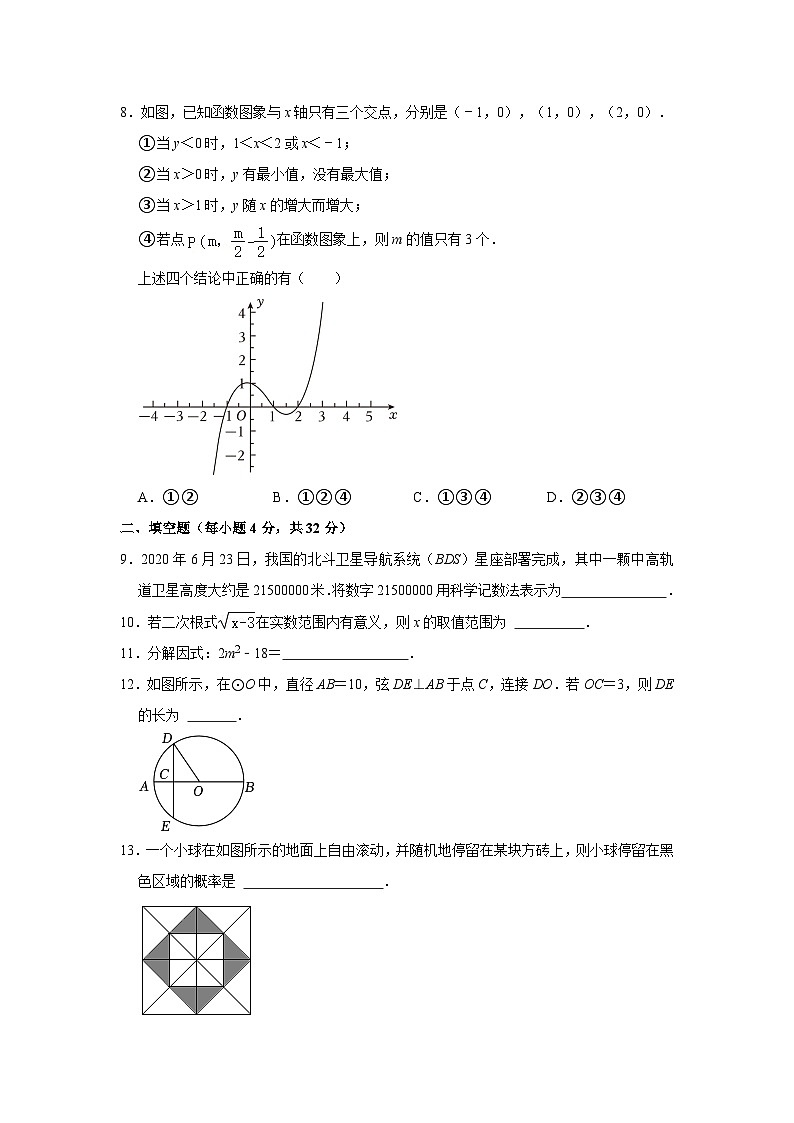
8．如图，已知函数图象与x轴只有三个交点，分别是（﹣1，0），（1，0），（2，0）．
①当y＜0时，1＜x＜2或x＜﹣1；
②当x＞0时，y有最小值，没有最大值；
③当x＞1时，y随x的增大而增大；
④若点在函数图象上，则m的值只有3个．
上述四个结论中正确的有（ ）
A．①②B．①②④C．①③④D．②③④
二、填空题（每小题4分，共32分）
9．2020年6月23日，我国的北斗卫星导航系统（BDS）星座部署完成，其中一颗中高轨道卫星高度大约是21500000米．将数字21500000用科学记数法表示为 ．
10．若二次根式在实数范围内有意义，则x的取值范围为 ．
11．分解因式：2m2﹣18＝ ．
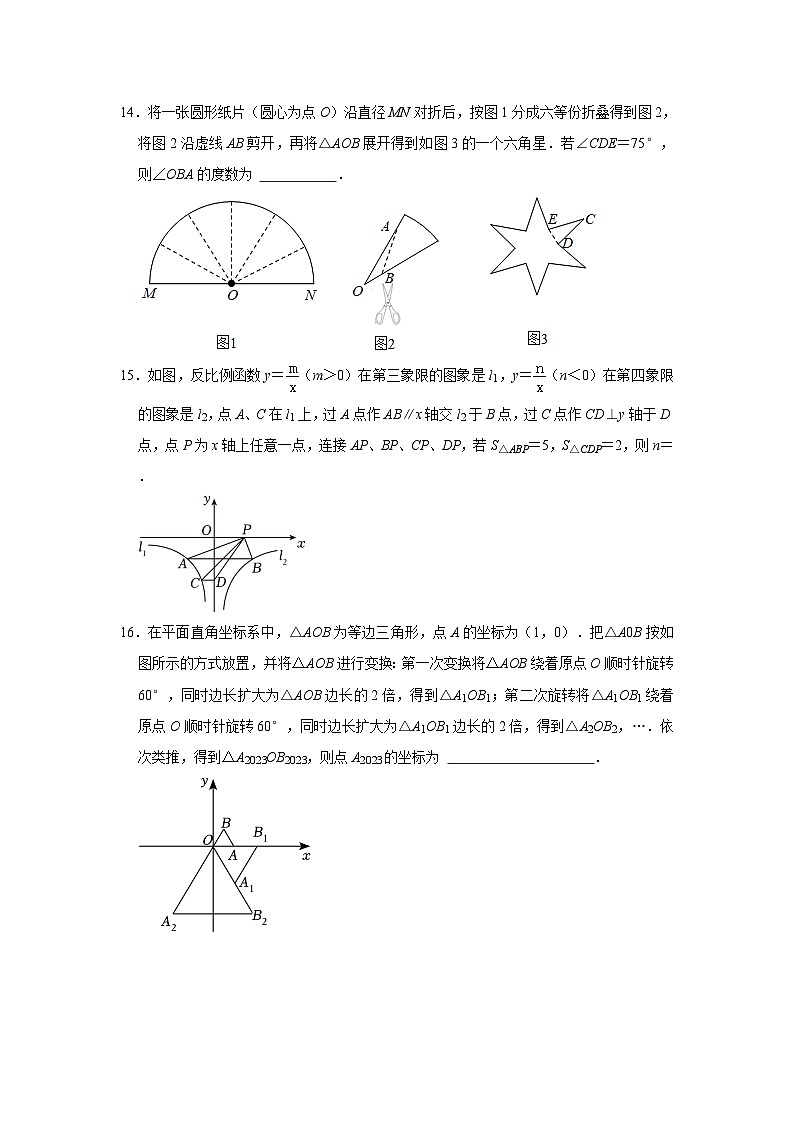
12．如图所示，在⊙O中，直径AB＝10，弦DE⊥AB于点C，连接DO．若OC＝3，则DE的长为 ．
13．一个小球在如图所示的地面上自由滚动，并随机地停留在某块方砖上，则小球停留在黑色区域的概率是 ．
14．将一张圆形纸片（圆心为点O）沿直径MN对折后，按图1分成六等份折叠得到图2，将图2沿虚线AB剪开，再将△AOB展开得到如图3的一个六角星．若∠CDE＝75°，则∠OBA的度数为 ．
15．如图，反比例函数y＝（m＞0）在第三象限的图象是l1，y＝（n＜0）在第四象限的图象是l2，点A、C在l1上，过A点作AB∥x轴交l2于B点，过C点作CD⊥y轴于D点，点P为x轴上任意一点，连接AP、BP、CP、DP，若S△ABP＝5，S△CDP＝2，则n＝ ．
16．在平面直角坐标系中，△AOB为等边三角形，点A的坐标为（1，0）．把△A0B按如图所示的方式放置，并将△AOB进行变换：第一次变换将△AOB绕着原点O顺时针旋转60°，同时边长扩大为△AOB边长的2倍，得到△A1OB1；第二次旋转将△A1OB1绕着原点O顺时针旋转60°，同时边长扩大为△A1OB1边长的2倍，得到△A2OB2，…．依次类推，得到△A2023OB2023，则点A2023的坐标为 ．
三、解答题
17．计算（4分）
．
18．解不等式组（4分）：．
19．先化简，再求值（8分）：，其中a＝，．
20．（10分）某同学家准备购买一辆新能源汽车．在预算范围内，收集了A，B两款汽车在2022年9月至2023年3月期间的国内销售量和网友对车辆的外观造型、舒适程度、操控性能、售后服务等四项评分数据，统计如下：
（1）数据分析：
①B款新能源汽车在2022年9月至2023年3月期间月销售量的中位数为 ；
②若将车辆的外观造型、舒适程度、操控性能，售后服务四项评分数据按1：3：3：3的比例统计，求A款新能源汽车四项评分数据的平均数．
（2）合理建议：
请你按照第（1）问中四项评分数据的比例，并结合销售量，在A、B两款汽车中给出你的推荐，并说明理由．
21．（10分）随着信息技术的迅猛发展，人们去商场购物的支付方式更加多样、便捷，现有“微信”、“支付宝”、“银行卡”和“现金”四种支付方式．
（1）若随机选一种方式进行支付，则恰巧是“现金”的概率是 ；
（2）在一次购物中，小嘉和小琪都想从“微信”、“支付宝”和“银行卡”三种支付方式中选一种方式进行支付，求出两人恰好选择同一种支付方式的概率（用画树状图法或列表法求解）．
22．（10分）如图，直线y＝x+m和抛物线y＝x2+bx+c都经过点A（1，0），B（3，2）．
（1）求m的值和抛物线的关系式；
（2）求不等式x2+bx+c＞x+m的解集（直接写出答案）．
23．（10分）如图，△ABC中，以AB为直径的⊙O交BC于点E，AE平分∠BAC，过点E作ED⊥AC于点D，延长DE交AB的延长线于点P．
（1）求证：PE是⊙O的切线；
（2）若，BP＝4，求CD的长．
24．（10分）实验是培养学生的创新能力的重要途径之一．如图是小红同学安装的化学实验装置，安装要求为试管略向下倾斜，试管夹应固定在距试管口的三分之一处．已知试管，AB＝30cm，BE＝AB，试管倾斜角α为10°．
（1）求酒精灯与铁架台的水平距离CD的长度；
（2）实验时，当导气管紧贴水槽MN，延长BM交CN的延长线于点F，且MN⊥CF（点C，D，N，F在一条直线上），经测得：DE＝21.7cm，MN＝8cm，∠ABM＝145°，求线段DN的长度．
（参考数据：sin10°≈0.17，cs10°≈0.98，tan10°≈0.18）
25．（10分）综合与实践：
问题情境
小莹妈妈的花卉超市以15元/盆的价格新购进了某种盆栽花卉，为了确定售价，小莹帮妈妈调查了附近A，B，C，D，E五家花卉店近期该种盆栽花卉的售价x与日销售量y情况，记录如下：
数据整理：
（1）请将以上调查数据按照一定顺序重新整理，填写在下表中：
模型建立
（2）分析数据的变化规律，探究出日销售量y与售价x之间的关系式．
拓广应用
（3）根据以上信息，小莹妈妈在销售该种花卉中．
①要想每天获得400元的利润，应如何定价？
②售价定为多少时，每天能够获得最大利润？
26．请阅读下列材料，完成相应的任务：
有这样一个题目：设有两只电阻，分别为R1和R2，问并联后的电阻值R是多少？
我们可以利用公式，求得R的值，也可以设计一种图形直接得出结果，具体如下：
如图①，在直线l上任取两点A、B，分别过点A、B作直线l的垂线，并在这两条垂线上分别截取AC＝R1，BD＝R2，且点C、D位于直线l的同侧，连接AD、BC，交于点E，过点E作EF⊥直线l，则线段EF的长度就是并联后的电阻值R．
证明：∵EF⊥l，CA⊥l，
∴∠EFB＝∠CAB＝90°，
又∵∠EBF＝∠CBA，
∴△EBF∽△CBA（依据1），
∴（依据2）．
同理可得：，
∴，
∴，
∴，
即：．
任务；
（1）上述证明过程中的“依据1”和“依据2”分别是指：
依据1： ；
依据2： ；
（2）如图②，两个电阻并联在同一电路中，已知R1＝3千欧，R2＝6千欧，请在图③中（1个单位长度代表1千欧）画出表示该电路图中总阻值R的线段长；
（3）受以上作图法的启发，小明提出了已知R1和R，求R2的一种作图方法，如图④，作△ABC，使∠C＝90°，AC＝BC＝R1，过点B作BC的垂线，并在垂线上截取BD＝R，使点D与点A在直线BC的同一侧，作射线AD，交CB的延长线于点E，则BE即为R2．你认为他的方法是否正确，若正确，请加以证明；若不正确，请说明理由．
27．（10分）定义：如果一个三角形中有两个内角α，β满足α+2β＝90°，那我们称这个三角形为“近直角三角形”．
（1）若△ABC是“近直角三角形”，∠B＞90°，∠C＝50°，则∠A＝ 度；
（2）如图1，在Rt△ABC中，∠BAC＝90°，AB＝3，AC＝4．若BD是∠ABC的平分线，
①求证：△BDC是“近直角三角形”；
②在边AC上是否存在点E（异于点D），使得△BCE也是“近直角三角形”？若存在，请求出CE的长；若不存在，请说明理由．
（3）如图2，在Rt△ABC中，∠BAC＝90°，点D为AC边上一点，以BD为直径的圆交BC于点E，连接AE交BD于点F，若△BCD为“近直角三角形”，且AB＝5，AF＝3，求tan∠C的值．
声明：试题解析著作权属所有，未经书面同意，不得复制发布日期：2024/4/28 7:37:14；用户：王立研；邮箱：rFmNt_U77fScWxT8l0DTCmjLXRs@；学号：258401售价（元/盆）
日销售量（盆）
A
20
50
B
30
30
C
18
54
D
22
46
E
26
38
售价（元/盆）





日销售量（盆）