浙江省中考数学总复习阶段检测3一次函数与反比例函数试题

这是一份浙江省中考数学总复习阶段检测3一次函数与反比例函数试题，共11页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1．若A(2x－5，6－2x)在第四象限，则x的取值范围是( )
A．x＞3 B．x＞－3 C．x＜－3 D．x＜3
2．已知下列函数：①y＝－eq \f(2,x)(x＞0)，②y＝－2x＋1，③y＝3x2＋1(x＜0)，④y＝x＋3，其中y随x的增大而减小的函数有( )
A．1个 B．2个 C．3个 D．4个
3．在同一直角坐标系中，一次函数y＝kx－k与反比例函数y＝eq \f(k,x)(k≠0)的图象大致是( )
4．已知函数y＝eq \f(m,x)图象如图，以下结论，其中正确有( )
①m＜0；②在每个分支上y随x的增大而增大；③若A(－1，a)，点B(2，b)在图象上，则a＜b；④若P(x，y)在图象上，则点P1(－x，－y)也在图象上．
A．4个 B．3个 C．2个 D．1个

第4题图 第5题图
5．已知反比例函数的图象经过点(－2，4)，当x＞2时，所对应的函数值y的取值范围是( )
A．－2＜y＜0 B．－3＜y＜－1 C．－4＜y＜0 D．0＜y＜1
6．一次函数y＝eq \f(4,3)x－b与y＝eq \f(4,3)x－1的图象之间的距离等于3，则b的值为( )
A．－2或4 B．2或－4 C．4或－6 D．－4或6
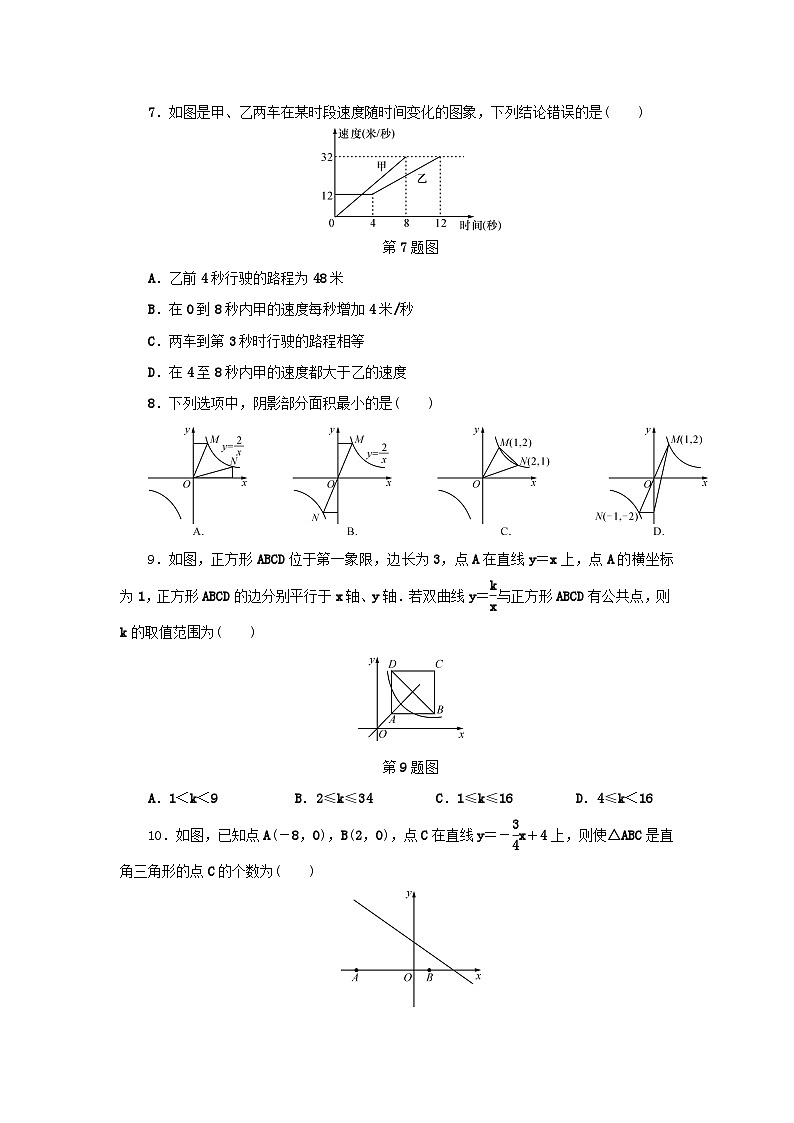
7．如图是甲、乙两车在某时段速度随时间变化的图象，下列结论错误的是( )
第7题图
A．乙前4秒行驶的路程为48米
B．在0到8秒内甲的速度每秒增加4米/秒
C．两车到第3秒时行驶的路程相等
D．在4至8秒内甲的速度都大于乙的速度
8．下列选项中，阴影部分面积最小的是( )
如图，正方形ABCD位于第一象限，边长为3，点A在直线y＝x上，点A的横坐标为1，正方形ABCD的边分别平行于x轴、y轴．若双曲线y＝eq \f(k,x)与正方形ABCD有公共点，则k的取值范围为( )
第9题图
A．1＜k＜9 B．2≤k≤34 C．1≤k≤16 D．4≤k＜16
如图，已知点A(－8，0)，B(2，0)，点C在直线y＝－eq \f(3,4)x＋4上，则使△ABC是直角三角形的点C的个数为( )
第10题图
A．1 B．2 C．3 D．4
二、填空题(本大题有6小题，每小题5分，共30分)
11．已知A(－1，m)与B(2，m－3)是反比例函数y＝eq \f(k,x)图象上的两个点．则m的值 .
12．如图，在平面直角坐标系中，菱形OABC的面积为12，点B在y轴上，点C在反比例函数y＝eq \f(k,x)的图象上，则k的值为 .
第12题图 第13题图 第14题图 第15题图
13．如图，点A(m，2)，B(5，n)在函数y＝eq \f(k,x)(k＞0，x＞0)的图象上，将该函数图象向上平移2个单位长度得到一条新的曲线，点A、B的对应点分别为A′、B′.图中阴影部分的面积为8，则k的值为 .
14．若直线y＝kx与四条直线x＝1，x＝2，y＝1，y＝2围成的正方形有公共点，则k的取值范围是 .
15．一辆慢车与一辆快车分别从甲、乙两地同时出发，匀速相向而行，两车在途中相遇后分别按原速同时驶往甲地，两车之间的距离S(km)与慢车行驶时间t(h)之间的函数图象如图所示，则快车到达甲地时，慢车距离甲地____________________km.
16．如图，直角坐标系xOy中，正方形OABC的边AB与反比例函数y＝eq \f(1,x)(x＞0)的图象交于点D，且AD∶DB＝1∶8，则：
第16题图
(1)点D的坐标为 ；
(2)设P是反比例函数图象上的动点，则线段PB长度的最小值是 .
三、解答题(本大题有8小题，第17～20题每题8分，第21题10分，第22、23题每题12分，第24题14分，共80分)
17．已知一次函数y＝kx＋b(k为常数，k≠0)的图象经过点A(2，2)，B(0，1)．
第17题图
(1)求该一次函数的解析式，并作出其图象；
(2)当0≤y≤2时，求x的取值范围．

18．在平面直角坐标系中，把横纵坐标都是整数的点称为“整点”．
(1)直接写出函数y＝eq \f(3,x)图象上的所有“整点”A1，A2，A3，…的坐标；
(2)在(1)的所有整点中任取两点，用树状图或列表法求出这两点关于原点对称的概率．
第18题图

如图，反比例函数y＝eq \f(k,x)与一次函数y＝ax＋b的图象交于点A(2，2)、Beq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)，n)).
第19题图
(1)求这两个函数解析式；
(2)将一次函数y＝ax＋b的图象沿y轴向下平移m个单位，使平移后的图象与反比例函数y＝eq \f(k,x)的图象有且只有一个交点，求m的值．

环保局对某企业排污情况进行检测，结果显示：所排污水中硫化物的浓度超标，即硫化物的浓度超过最高允许的1.0mg/L.环保局要求该企业立即整改，在15天以内(含15天)排污达标．整改过程中，所排污水中硫化物的浓度y(mg/L)与时间x(天)的变化规律如图所示，其中线段AB表示前3天的变化规律，从第3天起，所排污水中硫化物的浓度y与时间x成反比例关系．
第20题图
(1)求整改过程中硫化物的浓度y与时间x的函数表达式；
(2)该企业所排污水中硫化物的浓度，能否在15天以内不超过最高允许的1.0mg/L？为什么？

小明和爸爸从家步行去公园，爸爸先出发一直匀速前行，小明后出发．家到公园的距离为2500m，如图是小明和爸爸所走的路程s(m)与步行时间t(min)的函数图象．
第21题图
(1)直接写出小明所走路程s与时间t的函数关系式；
(2)小明出发多少时间与爸爸第三次相遇？
(3)在速度都不变的情况下，小明希望比爸爸早20min到达公园，则小明在步行过程中停留的时间需作怎样的调整？
22．如图，在矩形OABC中，OA＝3，OC＝2，F是AB上的一个动点(F不与A，B重合)，过点F的反比例函数y＝eq \f(k,x)(k＞0)的图象与BC边交于点E.
第22题图
(1)当F为AB的中点时，求该函数的解析式；
(2)当k为何值时，△EFA的面积最大，最大面积是多少？

如图，反比例函数y＝eq \f(k,x)(x＞0)的图象与直线y＝x交于点M，∠AMB＝90°，其两边分别与两坐标轴的正半轴交于点A，B，四边形OAMB的面积为6.
第23题图
(1)求k的值；
(2)点P在反比例函数y＝eq \f(k,x)(x＞0)的图象上，若点P的横坐标为3，∠EPF＝90°，其两边分别与x轴的正半轴，直线y＝x交于点E，F，问是否存在点E，使得PE＝PF？若存在，求出点E的坐标；若不存在，请说明理由．


24．某书店为了迎接“读书节”制定了活动计划，以下是活动计划书的部分信息：
(1)陈经理查看计划书时发现：A类图书的标价是B类图书标价的1.5倍，若顾客用540元购买的图书，能单独购买A类图书的数量恰好比单独购买B类图书的数量少10本，请求出A、B两类图书的标价；
(2)经市场调查后，陈经理发现他们高估了“读书节”对图书销售的影响，便调整了销售方案，A类图书每本标价降低a元(0＜a＜5)销售，B类图书价格不变，那么书店应如何进货才能获得最大利润？
阶段检测3 一次函数与反比例函数
一、1—5.ABABC 6—10.DCCCC
二、11.2 12.－6 13.2 14eq \f(1,2)≤k≤2 15.60
16．(1)eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,3)，3)) (2)2eq \r(2)
三、17.(1)∵点A(2，2)，点B(0，1)在一次函数y＝kx＋b(k为常数，k≠0)的图象上，∴eq \b\lc\{(\a\vs4\al\c1(2k＋b＝2，,b＝1，))解得eq \b\lc\{(\a\vs4\al\c1(k＝\f(1,2)，,b＝1，))∴一次函数的解析式为：y＝eq \f(1,2)x＋1其图象如下图所示： (2)∵k＝eq \f(1,2)＞0，∴一次函数y＝eq \f(1,2)x＋1的函数值y随x的增大而增大．当y＝0时，解得x＝－2；当y＝2时，x＝2.∴－2≤x≤2.即：当0≤y≤2时，x的取值范围是：－2≤x≤2.
第17题图
18．(1)由题意可得函数y＝eq \f(3,x)图象上的所有“整点”的坐标为：A1(－3，－1)，A2(－1，－3)，A3(1，3)，A4(3，1)；(2)所有的可能性如下图所示，由图可知，共有12种结果，关于原点对称的有4种，∴P(关于原点对称)＝eq \f(4,12)＝eq \f(1,3).
第18题图
19．(1)∵A(2，2)在反比例函数y＝eq \f(k,x)的图象上，∴k＝4.∴反比例函数的解析式为y＝eq \f(4,x).又∵点Beq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)，n))在反比例函数y＝eq \f(4,x)的图象上，∴eq \f(1,2)n＝4，解得：n＝8，即点B的坐标为eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)，8)).由A(2，2)、Beq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)，8))在一次函数y＝ax＋b的图象上，得：eq \b\lc\{(\a\vs4\al\c1(2＝2a＋b,8＝\f(1,2)a＋b))，解得：eq \b\lc\{(\a\vs4\al\c1(a＝－4,b＝10))，∴一次函数的解析式为y＝－4x＋10. (2)将直线y＝－4x＋10向下平移m个单位得直线的解析式为y＝－4x＋10－m，∵直线y＝－4x＋10－m与双曲线y＝eq \f(4,x)有且只有一个交点，令－4x＋10－m＝eq \f(4,x)，得4x2＋(m－10)x＋4＝0，∴Δ＝(m－10)2－64＝0，解得：m＝2或m＝18.
20．(1)分情况讨论：①当0≤x≤3时，设线段AB对应的函数表达式为y＝kx＋b；把A(0，10)，B(3，4)代入得eq \b\lc\{(\a\vs4\al\c1(b＝10,3k＋b＝4))，解得：eq \b\lc\{(\a\vs4\al\c1(k＝－2,b＝10))，∴y＝－2x＋10；②当x＞3时，设y＝eq \f(m,x)，把(3，4)代入得：m＝3×4＝12，∴y＝eq \f(12,x)；综上所述：当0≤x≤3时，y＝－2x＋10；当x＞3时，y＝eq \f(12,x)； (2)能；理由如下：令y＝eq \f(12,x)＝1，则x＝12＜15，故能在15天以内不超过最高允许的1.0mg/L.
21．(1)s＝eq \b\lc\{(\a\vs4\al\c1(50t（0≤t≤20），,1000（20