
2024年河北省廊坊市广阳区中考一模数学试题
展开本试卷分卷Ⅰ和卷Ⅱ两部分;卷Ⅰ为选择题,卷Ⅱ为非选择题.
本试卷满分为120分,考试时间为120分钟.
卷Ⅰ(选择题,共42分)
注意事项:1.答卷Ⅰ前,考生务必将自己的姓名、准考证号、科目填涂在答题卡上.考试结束,监考人员将试卷和答题卡一并收回.
2.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,答在试卷上无效.
一、选择题(本大题有16个小题,共42分.1—10小题各3分,11—16小题各2分,每小题给出的四个选项中,只有一项符合题目要求.)
1.-2的相反数是( )
A.2B.-2C.D.
2.“x与5的差的一半是正数”,用不等式可表示为( )
A.B.C.D.
3.数字240万用科学记数法表示应为( )
A.B.C.D.
4.杭州亚运会圆满闭幕后,某校调查了学生最喜爱的运动项目,根据统计结果绘得的扇形统计图如图所示.若最喜欢乒乓球的有30人,则最喜欢篮球的有( )
A.20人B.24人C.25人D.30人
5.把分解因式,正确的是( )
A.B.C.D.
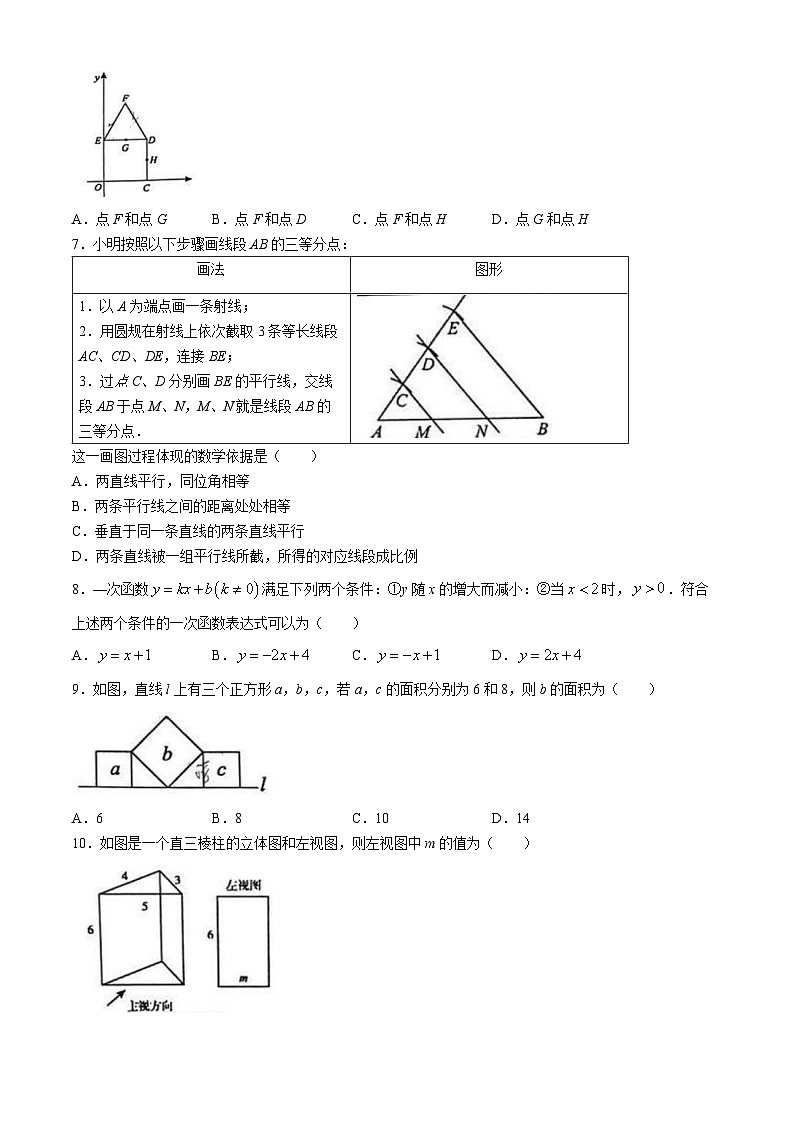
6.如图,四边形OCDE是边长为2的正方形,是边长为2的正三角形,点G,H分别是边DE,DC的中点,在点F,D,G,H四个点中,位于同一反比例函数图像上的两个点是( )
A.点F和点GB.点F和点DC.点F和点HD.点G和点H
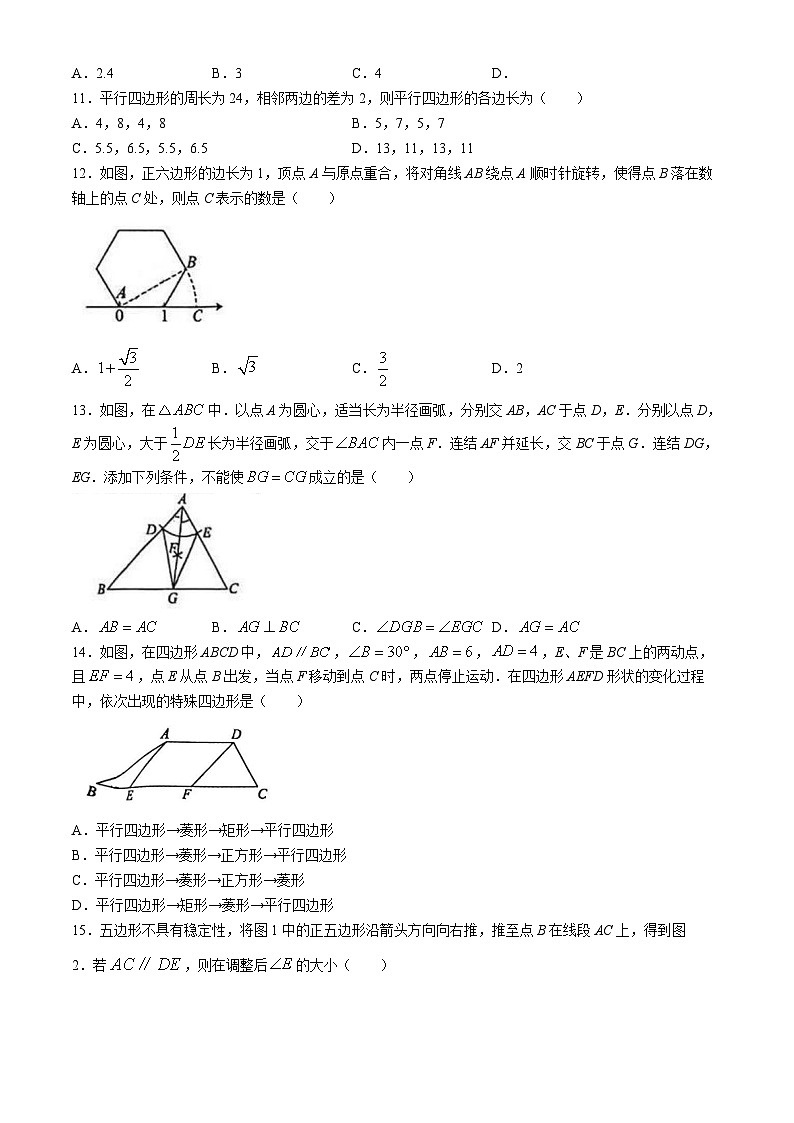
7.小明按照以下步骤画线段AB的三等分点:
这一画图过程体现的数学依据是( )
A.两直线平行,同位角相等
B.两条平行线之间的距离处处相等
C.垂直于同一条直线的两条直线平行
D.两条直线被一组平行线所截,所得的对应线段成比例
8.—次函数满足下列两个条件:①y随x的增大而减小:②当时,.符合上述两个条件的一次函数表达式可以为( )
A.B.C.D.
9.如图,直线l上有三个正方形a,b,c,若a,c的面积分别为6和8,则b的面积为( )
A.6B.8C.10D.14
10.如图是一个直三棱柱的立体图和左视图,则左视图中m的值为( )
A.2.4B.3C.4D.
11.平行四边形的周长为24,相邻两边的差为2,则平行四边形的各边长为( )
A.4,8,4,8B.5,7,5,7
C.5.5,6.5,5.5,6.5D.13,11,13,11
12.如图,正六边形的边长为1,顶点A与原点重合,将对角线AB绕点A顺时针旋转,使得点B落在数轴上的点C处,则点C表示的数是( )
A.B.C.D.2
13.如图,在中.以点A为圆心,适当长为半径画弧,分别交AB,AC于点D,E.分别以点D,E为圆心,大于长为半径画弧,交于内一点F.连结AF并延长,交BC于点G.连结DG,EG.添加下列条件,不能使成立的是( )
A.B.C.D.
14.如图,在四边形ABCD中,,,,,E、F是BC上的两动点,且,点E从点B出发,当点F移动到点C时,两点停止运动.在四边形AEFD形状的变化过程中,依次出现的特殊四边形是( )
A.平行四边形→菱形→矩形→平行四边形
B.平行四边形→菱形→正方形→平行四边形
C.平行四边形→菱形→正方形→菱形
D.平行四边形→矩形→菱形→平行四边形
15.五边形不具有稳定性,将图1中的正五边形沿箭头方向向右推,推至点B在线段AC上,得到图2.若,则在调整后的大小( )
A.减少了12°B.增加了12°C.减少了15°D.增加了15°
16.将二次函数的图象在x轴上方的部分沿x轴翻折后,所得新函数的图象如图所示.当直线与新函数的图象恰有3个公共点时,b的值为( )
A.或-3B.或3C.或3D.或-3
卷Ⅱ(非选择题,共78分)
二、填空题(17-18题每题3分,19题每空2分,共10分.)
17.如果分式的值为0,则x的值为______.
18.如图,一束光线从点出发,经过y轴上的点反射后经过点,则的值是______.
19.在某次数学探究活动中,小明将一张斜边为4的等腰直角三角形硬纸片剪切成如图所示的四块(其中D,E,F分别为AB,AC,BC的中点,G,H分别为DE,BF的中点),小明将这四块纸片重新组合拼成四边形(相互不重叠,不留空隙),则所能拼成的四边形中周长的最小值为______,最大值为______.
三、解答题(本大题共7题,共计68分,解答应写出文字说明、证明过程或演算步骤)
20.(8分)六一到了,嘉嘉和同学要表演节目.嘉嘉骑车到同学家拿东西,再到学校,她从自己家出发,向东骑了2km到达淇淇家,继续向东骑了1.5km到达小敏家,然后又向西骑了4.5km到达学校.演出结束后又向东骑回到自己家.
(1)以嘉嘉家为原点,向东为正方向,用1个单位长度表示1km,在图中的数轴上,分别用点A表示出淇淇家,用点B表示出小敏家,用点C表示出学校的位置;
(2)求淇淇家与学校之间的距离;
(3)如果嘉嘉骑车的速度是300m/min,那么嘉嘉骑车一共用了多长时间?
21.(7分)(1)请用含x和y的代数式来表示阴影部分的面积.
(2)当,时,阴影部分的面积是多少?
22.(7分)如图,是一个竖直放置的钉板,其中,黑色圆点表示钉板上的钉子,,,,…,,分别表示相邻两颗钉子之间的空隙,这些空隙大小均相等,从入口处投放一个直径略小于两颗钉子之间空隙的圆球,圆球下落过程中,总是碰到空隙正下方的钉子,且沿该钉子左右两个相邻空隙继续下落的机会相等,直至圆球落入下面的某个槽内.
(1)求圆球落入的概率.
(2)用画树状图的方法,求圆球落入③号槽内的概率.
23.(9分)“刻漏”是我国古代的一种利用水流计时的工具.综合实践小组用甲、乙两个透明的竖直放置的容器和一根带节流阀(控制水的流速大小)的软管制作了如图所示的简易计时装置.他们设计了如下的实验:先在甲容器里加满水,此时水面高度为30cm,开始放水后每隔10min观察一次甲容器中的水面高度,获得的数据如表,发现水面高度h(cm)与流水时间t(min)(t为正整数)之间满足一次函数关系.
(1)求水面高度h与流水时间t之间的函数关系式;
(2)按此速度,流水时间为1小时时,水面高度为多少厘米?
(3)按此速度,经过多长时间,甲容器内的水恰好流完?
24.(10分)一酒精消毒瓶如图1,AB为喷嘴,为按压柄,BE和EF为导管,其示意图如图2,,,.当按压柄按压到底时,此时(如图3).
(1)求BD旋转到过程中扫过的面积;
(2)求点D到直线EF的距离(结果精确到0.1cm)(参考数据:,,,,,)
25.(13分)如图,抛物线与x轴交于,两点,与y轴交于点C.P是抛物线上的任意一点(不与点C重合),点P的横坐标为m,抛物线上点C与点P之间的部分(包含端点)记为图象G.
(1)求抛物线的解析式;
(2)当m符合什么条件时,图象G的最大值与最小值的差为4?
(3)将线段AB先向左平移1个单位长度,再向上平移5个单位长度,得到线段.若抛物线平移后与线段有两个交点,且这两个交点恰好将线段三等分,求抛物线平移的最短路程;
26.(14分)综合与实践课上,老师让同学们以“图形的折叠与变换”为主题开展数学活动.
(1)操作判断
操作一:如图1,将矩形纸片ABCD折叠,使AB落在边AD上,点B与点E重合,折痕为AF﹔根据以上操作:四边形AEFB的形状是______;
操作二:沿EF剪开,将四边形AEFB折叠,使边AB,AE都落在四边形的对角线AF上,折痕为AG,AH,连接GH,如图2.
根据以上操作:的度数为______;线段BG、GH、EH的数量关系是______.
(2)迁移探究
如图3,在BF、EF上分别取点I、J,使和图2中的相等,连接IJ,探究线段BI,IJ,EJ之间的数量关系,并说明理由.
(3)拓展应用
在(2)的探究下,连接对角线BE,若图3中的的边AI,AJ分别交对角线BE于点K,R,将纸片沿对角线BE剪开,如图4,若,,直接写出KR的长.
参考答案
一、选择题
1-5 ABDBD 6-10 DDBDA 11-16 BBDABA
二、填空题
17.1 18.-1 19.8
三、解答题
20.解:(1)根据题意得:淇淇家的位置对应的数为2,小敏家的位置对应的数为3.5,学校的位置对应的数为-1,如图所示:
(2).
答:淇淇家与学校之间的距离是3km.
(3),,.
答:嘉嘉骑车一共用了30min.
21.解:(1)
(2)当,时,
22.解(1)
(2)画树状图得:
所以圆球下落过程中共有8种路径,其中落入③号槽内的有3种,所以圆球落入③号槽内的概率为.
23.(1)设水面高度h与流水时间t之间的函数关系式为,
把,代入得:解得
∴水面高度h与流水时间t之间的函数关系式为;
(2)当分钟时,,
∴流水时间为1小时时,水面高度为18厘米;
(3)当,时,的,
∴,即经过150min,甲容器内的水恰好流完.
24.(1)解:∵,,
∴
∵,∴,
∵,∴BD旋转到扫过的面积为,
(2)过D作于G,过E作于H.
中,,
中,,
∴,
∵,∴点D到直线EF的距离约为7.3cm
25.(1)解:将,代入,
∴,解得,
∴抛物线的解析式为;
(2)解:在中,令,则,∴,
∵,∴抛物线的顶点为,
当时,,∴或,
当时,图象G的最大值为9,最小值为,
∴,解得或,
∴时,图象G的最大值与最小值的差为4:
当时,图象G的最大值为9,最小值为5,图象G的最大值与最小值的差为4:
当时,图象G的最大值为,最小值为5,
∴,解得(舍去);
当时,图象G的最大值为5,最小值为,
∴,
解得或
此时Р点与C点位于对称轴同侧,所以舍去
综上所述:或时,图象G的最大值与最小值的差为4:
(3)解:∵,,
∴将线段AB先向左平移1个单位长度,再向上平移5个单位长度可得,,
∴线段的两个三等分点坐标为,,
设平移后的抛物线解析式为,
∵抛物线平移后与线段有两个交点,且这两个交点恰好将线段三等
∴,解得,
∴平移后的抛物线解析式为,其顶点为,
而抛物线的顶点为,
∴平移前,后抛物线的顶点之间的距离为,
∴抛物线平移的最短路程为;
26.解:(1)正方形;45∘,;
(2),理由如下:
如图,将顺时针旋转90°得到
由旋转的性质可得,,,,
∵四边形ABFE为正方形,
∴,∴,
∴,
即、B、F三点在同一直线上,
由(1)中结论可得,
∴,∴,∴,
在和中,
∴,∴,
∵,∴;
(3)
画法
图形
1.以A为端点画一条射线;
2.用圆规在射线上依次截取3条等长线段AC、CD、DE,连接BE;
3.过点C、D分别画BE的平行线,交线段AB于点M、N,M、N就是线段AB的三等分点.
流水时间
0
10
20
30
40
…
水面高度(观察值)
30
28
26
24
22
…
2023年河北省廊坊市广阳区中考二模数学试题: 这是一份2023年河北省廊坊市广阳区中考二模数学试题,共15页。
2023年河北省廊坊市广阳区中考数学一模试卷(含答案): 这是一份2023年河北省廊坊市广阳区中考数学一模试卷(含答案),共27页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2023年河北省廊坊市广阳区中考数学一模试卷: 这是一份2023年河北省廊坊市广阳区中考数学一模试卷,共26页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












