+湖南省张家界市永定区2023-2024学年八年级下学期期中考试数学试题

这是一份+湖南省张家界市永定区2023-2024学年八年级下学期期中考试数学试题，共10页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
考生注意：本卷共三道题，满分120分，时量120分钟。
一、选择题（本大题共10个小题，每小题3分，满分30分．请将正确答案的字母代号填在下表中．）
1．中国航天取得了举世瞩目的成就，为人类和平贡献了中国智慧和中国力量，下列是有关中国航天的图标，其文字上方的图案是中心对称图形的是（ ）
A．中国探火CMEPB．中国探月CLEP
C．中国行星探测MARSD．中国火箭CHINAROCKET
2．若直角三角形的一个锐角等于，则它的另一个锐角等于（ ）
A．B．C．D．
3．如图，于点B，于D，若，且，，则的长为（ ）
A．1B．4
C．D．
4．下列命题是真命题的是（ ）
A．相等的角是对顶角B．若，则
C．两边分别相等的两个直角三角形全等D．同旁内角互补，两直线平行
5．下列各组数中，是勾股数的一组（ ）
A．0.3，0.4，0.5B．1，，2
C．6，8，10D．2，2，
6．如图，将平行四边形的一边延长至点E，若，则（ ）
A．B．
C．D．
7．如图，网格图中每个小正方形的边长均为1，以为半径的扇形经过平移到达扇形的位置，那么图中阴影部分的面积是（ ）．
A．8B．6C．6.5D．7.5
8．如图，数轴上点A表示的数是，，，以点O为圆心，为半径画弧，与数轴的负半轴相交，则交点P所表示的数是（ ）
A．B．
C．D．
9．如图，在中，点D是的中点，若，则的度数为（ ）
A．B．
C．D．
10．如图，在Rt△ABC中，∠BAC=90°，且AB=3，AC=4，D是斜边 BC上的一个动点，过点D分别作 DM⊥AB于点M，DN⊥AC于点N，连接 MN，则线段 MN 的最小值为（ ）
A．B．
C．3D．4
二、填空题（本大题共8小题，每小题3分，满分24分）
11．如图，在一个高3米，长4米的楼梯表面铺地毯，则该地毯的长度至少是 米．

11题图 13题图 15题图
12．一个多边形的每一个内角为，则这个多边形的内角和为 ．
13．如图所示的网格是正方形网格，A，B，C，D是网格线交点．若AB=1，则四边形ABCD的面积为 ．
14．等腰三角形腰长为10，腰上的高为8，则这个等腰三角形底边长为 ．
15．如图，在中，的平分线交BC于点E，若，，则的周长为 ．
16．在中，，以顶点A为圆心，适当长为半径画弧，分别交于点E，F；再分别以点E，F为圆心，大于的长为半径画弧，两弧交于点P，作射线交于点D．若，则点D到的距离是 ．

16题图 17题图
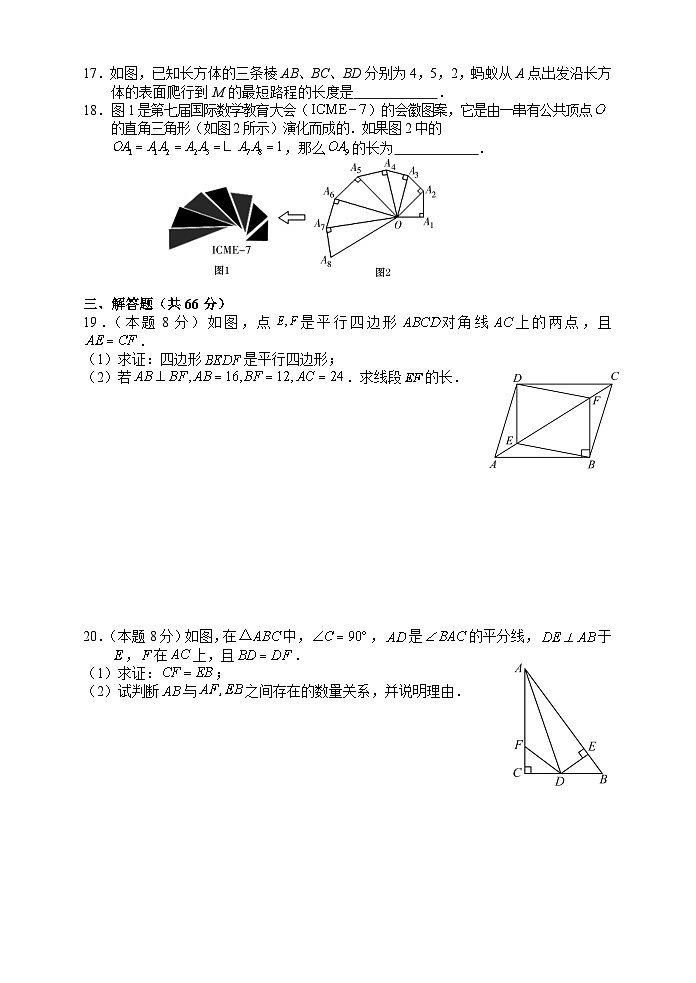
17．如图，已知长方体的三条棱AB、BC、BD分别为4，5，2，蚂蚁从A点出发沿长方体的表面爬行到M的最短路程的长度是 ．
18．图1是第七届国际数学教育大会（）的会徽图案，它是由一串有公共顶点的直角三角形（如图2所示）演化而成的．如果图2中的，那么的长为 ．

三、解答题（共66分）
19．（本题8分）如图，点是平行四边形对角线上的两点，且．
（1）求证：四边形是平行四边形；
（2）若．求线段的长．
20．（本题8分）如图，在中，，是的平分线，于，在上，且．
（1）求证：；
（2）试判断与之间存在的数量关系，并说明理由．
21．（本题6分）如图，四边形区域是音乐广场的一部分，现在要在这一区域内建一个喷泉，要求喷泉到两条道路，的距离相等，且到入口A、的距离相等请确定喷泉的位置P．
22．（本题7分）如图，在中，E，F分别是边上的点，且，连接相交于点G，连接相交于点H，连接．求证：
23．（本题9分）用不同的方式表示同一图形的面积可以解决线段长度之间关系的有关问题，这种方法称为等面积法，这是一种重要的数学方法．
（1）如图1是著名的“赵爽弦图”，由四个全等的直角三角形拼成，则： ， ；（此两空均用含，，的代数式表示，不用化简）根据面积相等，可知 （化简），故验证了勾股定理．
（2）如图2，在中，，是边上的高，，，求的长；
（3）如图1，，，直接写出的值．
24．（本题8分）如图，一架云梯斜靠在一面墙上，且云梯长，云梯底端到墙的距离为7m．
（1）这架云梯的顶端到地面的距离有多高？
（2）如果云梯的顶端A到下滑到A＇处，那么它的底部在水平方向也滑动了吗？
25．（本题10分）如图，在四边形中，，，，点P从点D出发，以的速度向点A运动；点M从点B同时出发，以相同的速度向点C运动，当其中一个动点到达端点时，两个动点同时停止运动．设点P的运动时间为t（单位：s）．
（1）四边形能否为矩形？请说明理由；
（2）四边形能否为平行四边形？请说明理由。
26．（本题10分）如图，△ABC中，∠ABC，∠ACB的平分线交于O点，过O点作EF∥BC交AB，AC于E，F．
（1）（本小题3分）如图①，当AB=AC时图中有 个等腰三角形．
（2）（本小题3分）如图②，写出EF与BE、CF之间关系式，并说明理由．
（3）（本小题4分）如图③，若△ABC中∠ABC的平分线BO与三角形外角平分线CO交于O，过O点作OE∥BC交AB于E，交AC于F．EF与BE、CF关系又如何?说明你的理由．
题 号
一
二
三
总 分
得 分
题号
1
2
3
4
5
6
7
8
9
10
答案
永定区2024年春季学期八年级期中质量监测试卷
数学参考答案
一、选择题（本大题共10个小题，每小题3分，满分30分．请将正确答案的字母代号填在下表中．）
二、填空题
11．7 12．13．14．或
15．5216．317．18．3
三、解答题
19．（1）证明：如图所示，连接交于O，
∵四边形是平行四边形，
∴，
∵，
∴，即，
∴四边形是平行四边形；
（2）解：∵，
∴，
∵，
∴，
∵，
∴，
∴．
20．（1）证明：是的平分线，，，
，
在和中，
，
，
；
（2）解：，
理由如下：在和中，
，
，
，
．
21．如图所示：P点即为所求．

22．证明：如图，连接，
∵四边形是平行四边形，
∴，．
∵，
∴．
∵
∴四边形和四边形都是平行四边形，
∴，
∴是的中位线，
∴
23．（1）解：∵如图1是著名的“赵爽弦图”，由四个全等的直角三角形拼成，
∴，
∴；
则
∵，
∴；
（2）解：在中，，
∴
∵是边上的高，
∴
即
（3）解：∵
∴
∵
∴
结合（1）结论
∴
24．（1）解∶在中，由勾股定理得，
即，
所以 ，
即这架云梯的顶端到地面的距离有高；
（2）解：梯子的底部在水平方向不是滑动了．理由：
令云梯的顶端下滑了至点，则
，
在中，由勾股定理得，
即
所以
，
即梯子的底端在水平方向也滑动了．
∴梯子的底部在水平方向不是滑动了．
25．（1）解：四边形能为矩形，理由如下：
当时，，
解得：，
∵，，
∴四边形能为平行四边形
又∵，
∴四边形能为矩形．
（2）解：四边形能为平行四边形，理由如下：
当时，，
解得：，
∵，，
∴四边形能为平行四边形．
26．解：（1）当AB=AC时，图中有5个等腰三角形．
如图1，由AB=AC，可得∠ABC=∠ACB，
又∵OB、OC分别平分∠ABC、∠ACB，
∴∠EBO=∠OBC=∠FCO=∠OCB，
根据EF∥BC，可得∠OEB=∠OBC=∠EBO，∠FOC=∠FCO=∠BCO，
由此可得出△ABC，△OBC，△EBO，△CFO，△AEF都是等腰三角形．
故答案为：5；
（2）关系式：EF=BE+CF
如图，∵EF∥BC，
∴∠2=∠3，
又∵∠1=∠2，
∴∠1=∠3，
∴OE=BE，
在△CFO中，同理可证OF=CF，
∵EF=EO+FO，
∴EF=BE+CF；
（3）关系式：EF=BE-CF
如图，∵OE∥BC，
∴∠5=∠6，
又∠4=∠5，
∴∠4=∠6，
∴OE=BE，
在△CFO中，同理可证OF=CF，
∵EF=EO-FO，
∴EF=BE-CF．
题号
1
2
3
4
5
6
7
8
9
10
答案
D
A
C
D
C
C
B
C
A
A