初中数学沪科版七年级下册第6章 实数6.2 实数课时作业

这是一份初中数学沪科版七年级下册第6章 实数6.2 实数课时作业，共15页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

一、单选题
1．下列语句或等式①；②的立方根是；③的算术平方根是8；④与数轴上的点一一对应的数是有理数；⑤平方根是它本身的数有和0；⑥9的平方根是，正确的有（ ）
A．2个B．3个C．4个D．5个
2．在下列各数中：0.111…，，，，3.1415926，2.010101…（相邻两个0之间有1个1），76.01020304050607…，．是无理数的有（ ）
A．3个B．4个C．5个D．6个
3．在下列各式中正确的是（ ）
A．B．C．D．
4．如图，数轴上的点P表示下列四个无理数中的一个，这个无理数是（ ）
A．B．C．D．π
5．已知，那么的值为（ ）
A．-1B．1C．D．
6．已知，，则（ ）
A．B．C．D．
7．如图，圆的直径为1个单位长度，该圆上的点A与数轴上表示－1的点重合，将该圆沿数轴滚动1周，点A到达点处，则点表示的数为（ ）
A．π－1B．－π－1或1－πC．1－πD．π－1或－π－1
8．若与互为相反数，则的值为（ ）
A．或3B．或5C．D．
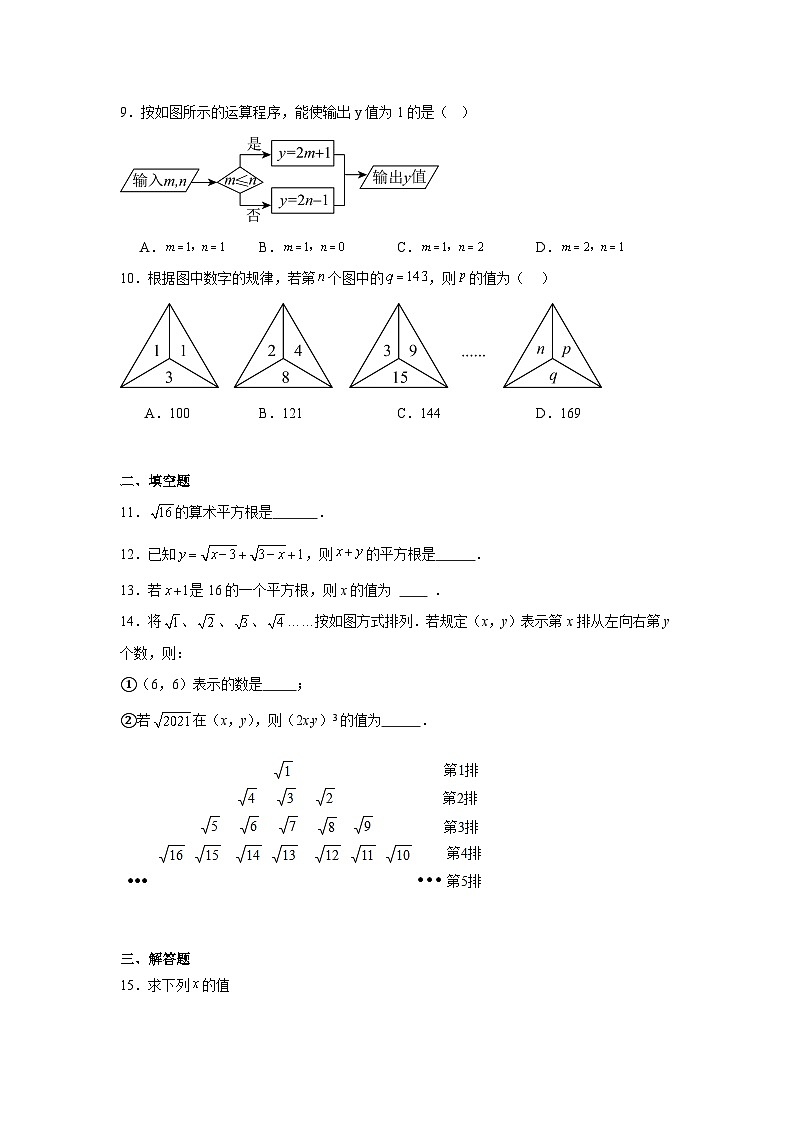
9．按如图所示的运算程序，能使输出y值为1的是（ ）
A．B．C．D．
10．根据图中数字的规律，若第个图中的，则的值为（ ）
A．100B．121C．144D．169
二、填空题
11．的算术平方根是 ．
12．已知，则的平方根是 ．
13．若是16的一个平方根，则x的值为 ．
14．将、、、……按如图方式排列．若规定（x，y）表示第x排从左向右第y个数，则：
①（6，6）表示的数是 ；
②若在（x，y），则（2x﹣y）3的值为 ．
三、解答题
15．求下列的值
(1)
(2)
16．计算
(1)
(2)
17．已知某数的两个平方根分别为和．
(1)求a的值，并求这个正数．
(2)求的立方根．
18．已知是的算术平方根，是的立方根，求的平方根．
19．化简求值：
(1)已知a是的整数部分，，求的平方根．
(2)已知：实数a，b在数轴上的位置如图所示，化简：．
20．小丽想用一块面积为900 cm2的正方形纸片，沿着边的方向裁出一块面积为600 cm2的长方形纸片，使它的长宽之比为4∶3，她不知道是否裁得出来，正在发愁，小明见了说：“别发愁，一定能用这块正方形纸片裁出需要的长方形纸片．”你同意小明的说法吗？小丽能用这块纸片裁出符合要求的纸片吗？
21．求下列各式的值．
(1)若a与b互为相反数，c与d互为倒数，x的绝对值等于5，求的值；
(2)若的立方根是3，的算术平方根是4，求的平方根；
(3)如图，在方格中阴影正方形的边长是 ，它的整数部分是 ，小数部分是 （小正方格的边长为1个长度单位）．
22．如图是一个数值转换器．
(1)当输入x＝25时，求输出的y的值；
(2)是否存在输入x的值后，始终输不出y的值？如果存在，请直接写出所有满足要求的x值；如果不存在，请说明理由；
(3)输入一个两位数x，恰好经过三次取算术平方根才能输出无理数y，则x＝________(只填一个即可)．
23．先观察下列等式，再回答下列问题：
①；
②；
③．
(1)请你根据上面三个等式提供的信息，猜想的结果，并验证；
(2)请你按照上面各等式反映的规律，试写出一个用n（n为正整数）表示的等式；
(3)请利用上述规律来计算（仿照上式写出过程）．
参考答案：
1．A
【分析】本题考查了平方根、立方根、算术平方根、实数与数轴，根据平方根、立方根、算术平方根、实数与数轴的相关知识点，逐一判断即可得到答案．
【详解】解：，故①错误，不符合题意；
，故②正确，符合题意；
，
的算术平方根是，故③错误，不符合题意；
与数轴上的点一一对应的数是实数，故④错误，不符合题意；
平方根是它本身的数是0，故⑤错误，不符合题意；
9的平方根是，故⑥正确，符合题意；
综上所述，正确的有②⑥，共2个，
故选：A．
2．A
【分析】无限不循环小数叫做无理数，有理数是整数与分数的统称．即有限小数和无限循环小数是有理数，而无限不循环小数是无理数．由此即可判定选择项．
【详解】解：﹣0.111…，3.1415926，2.010101…（相邻两个0之间有1个1），是分数，属于有理数；
，是整数，属于有理数；
无理数有，3π，76.01020304050607…，共3个．
故选：A．
【点睛】此题主要考查了无理数的定义．解题的关键是掌握无理数的定义，其中初中范围内学习的无理数有：π，2π等；开方开不尽的数；以及像0.1010010001…，等有这样规律的数．
3．D
【分析】根据平方根及算术平方根的性质可求解．
【详解】解：根据平方根及算术平方根的性质可知，，，，
观察四个选项，只有选项D正确，
故选：D．
【点睛】本题考查了算术平方根的定义，要注意正确区分平方根与算术平方根，解题的关键是掌握算术平方根的定义．
4．B
【分析】先根据数轴确定点P对应的数的大小，再结合选项进行判断即可．
【详解】解：由数轴可得，点P对应的数在1与2之间，
A.，故本选项不符合题意；
B. ，故此选项符合题意；
C. ，故本选项不符合题意；
D. ，故本选项不符合题意；
故选：B
【点睛】本题主要考查了实数与数轴，无理数的估算，正确确定点P对应的数的大小是解答本题的关键．
5．A
【分析】根据算术平方根和绝对值的非负性，确定a、b的值，再代入代数式求值即可.
【详解】解：由题意得：a+2=0，b-1=0，即a=-2，b=1
所以，
故答案为A.
【点睛】本题主要考查了非负数的性质，利用非负数的性质确定待定的字母的值是解答的关键
6．D
【分析】根据根号内的小数点移动规律即可求解，算术平方根的规律为，根号内的小数点移动2位，对应的结果小数移动1位，小数点的移动方向保持一致．
【详解】解：∵，
∴，
故选：D．
【点睛】本题考查了算术平方根的应用，掌握小数点的移动规律是解题的关键．
7．D
【分析】该圆沿数轴滚动一周，并没有说明方向，要考虑全面，排除A、C，根据圆的周长公式得出圆的周长是π，所以有-1+π，由此可得结论．
【详解】解：圆的周长C=πd=π，
圆向右滚动时，表示的数为-1+π，即π-1，
圆向左滚动时，表示的数为-1-π，即-π-1，
故选：D．
【点睛】本题考查数轴和圆的周长，分类讨论思想等，解题关键是掌握数轴的特点．
8．D
【分析】此题利用立方根知识：一个数的立方根与它本身的符号相同，据此知道（1-2x）和（3x-5）也互为相反数，列方程求解即可．
【详解】∵与互为相反数，
∴（1-2x）和（3x-5）也互为相反数，
即（1-2x）+（3x-5）=0，
解得：x=4，
∴=1-2=-1；
故选：D．
【点睛】此题考查立方根的相关知识，一个数的立方根与它本身的符号相同是此题解题的关键．
9．D
【分析】逐项代入，寻找正确答案即可.
【详解】解：A选项满足m≤n，则y=2m+1=3；
B选项不满足m≤n，则y=2n-1=-1；
C选项满足m≤n，则y=2m+1=3；
D选项不满足m≤n，则y=2n-1=1；
故答案为D；
【点睛】本题考查了根据条件代数式求值问题，解答的关键在于根据条件正确地代入代数式及代入的值.
10．B
【分析】分别分析n的规律、p的规律、q的规律，再找n、p、q之间的联系即可．
【详解】解：根据图中数据可知：
则，，
∵第个图中的，
∴，
解得：或(不符合题意，舍去)
∴，
故选：B．
【点睛】本题主要考查数字之间规律问题，将题中数据分组讨论是解决本题的关键．
11．2
【分析】根据算术平方根的运算法则，直接计算即可．
【详解】解：∵，4的算术平方根是2，
∴的算术平方根是2．
故答案为：2．
【点睛】此题考查了求一个数的算术平方根，这里需注意：的算术平方根和16的算术平方根是完全不一样的；因此求一个式子的平方根、立方根和算术平方根时，通常需先将式子化简，然后再去求，避免出错．
12．
【分析】根据根式的非负性可求出，的值，进而可求出答案．
【详解】解：∵，且根号下不能为负，
∴，，
∴，
∴，
∴，
∴的平方根是，
故答案为：．
【点睛】本题考查根式的非负性，以及计算一个数的平方根，能够根据根式的非负性计算出未知数的值是解决本题的关键．
13．3或/或3
【分析】根据平方根的定义，可得，进而即可求解．
【详解】解：∵是16的一个平方根，
∴，
∴x的值为3或．
【点睛】本题主要考查平方根的定义，掌握一个数的平方根有两个，它们互为相反数是关键．
14．
【分析】观察式子，得到如下规律，第排的个数为个，前排的总数为个，奇数排是从左到右依次增大排列，偶数排是从右到左依次增大排列，根据规律求解即可．
【详解】解：观察式子可得，
第1排的个数为，前1排的总数为，
第2排的个数为，前2排的总数为，从右到左依次增大排列，
第3排的个数为，前3排的总数为，从左到右依次增大排列，
第4排的个数为，前4排的总数为，从右到左依次增大排列，
……
第排的个数为个，前排的总数为个，奇数排是从左到右依次增大排列，偶数排是从右到左依次增大排列，
（6，6）表示第6排从左向右第6个数
前5排的总数为25，第6排的个数为11个，为偶数排，从右向左依次增大，
第6排中，从左向右第6个数，也就是从右向左第6个数，
所以（6，6）表示的数为；
因为，
所以是在第45排，即
第45排，为奇数排，从左向右依次增大，
因为，所以
将，代入得
故答案为：，
【点睛】此题考查了数字类规律的探索问题，涉及了有理数的乘方，算术平方根，解题的关键是理解题意，正确找出数字的规律．
15．(1)，
(2)
【分析】
（1）首先移项，然后利用直接开平方，即可求出答案；
（2）先直接开立方，即可求出答案．
【详解】（1），
，
，
，．
（2），
，
．
【点睛】本题主要考查了解方程，熟练掌握求平方根和求立方根的方法是解本题的关键．
16．(1)
(2)
【分析】（1）先计算乘方与开方，并去绝对值符号，再计算加减即可．
（2）先计算开方与乘方，再计算加减即可．
【详解】（1）解：原式
；
（2）解：原式
．
【点睛】本题考查实数的混合运算，求绝对值，平方根和立方根，熟练掌握实数运算法则是解题的关键．
17．(1)，169
(2)
【分析】本题考查的是平方根、立方根．
（1）根据一个正数的两个平方根互为相反数得到关于a的方程，求出a的值即可得到答案；
（2）先求出的值，再根据立方根的定义进行求解即可．
【详解】（1）解：由题意，得，
解得：
∴，
∴则这个数是：．
（2）由（1）知，
∴
∵
∴的立方根是．
18．
【分析】本题考查了立方根与平方根，正确理解立方根与平方根的意义是解题的关键．根据题意可得，，解得，，然后代入求出、进行求解．
【详解】解：由题意可得，
，
，
，
的平方根为．
19．(1)
(2)
【分析】（1）先估算出的取值范围，求出a的值；由于，根据算术平方根的定义可求b，再代入计算，进一步求平方根即可．
（2）利用数轴得出各项符号，进而利用二次根式和绝对值的性质化简．
【详解】（1）∵，
∴，
∴，
∴，
∵，
∴，
∴，
∴的平方根是；
（2）由数轴可得：，
则，
则
．
【点睛】本题考查了算术平方根与平方根的定义，以及估算无理数的大小，熟练掌握无理数的估算方法是解题的关键．
20．见解析
【详解】试题分析：根据算术平方根的概念求出正方形的边长，根据长方形纸片的面积求出边长，计算比较得到答案．
试题解析：同意小明的说法．
面积为900 cm2的正方形纸片的边长为30 cm.设长方形的长为4x cm，宽为3x cm，根据边长与面积的关系得4x×3x＝600.解得x＝.因此长方形纸片的长为4cm.
∵＜7.5，
∴4＜30.
∴小丽能用这块纸片裁出符合要求的纸片．
21．(1)或
(2)的平方根是
(3)，3，
【分析】本题主要考查实数的性质，正确掌握相关的定义是解题的关键．
（1）直接利用相反数、互为倒数、绝对值的性质代数计算；
（2）直接利用立方根和平方根的定义的定义求解即可；
（3）利用勾股定理进行求解．
【详解】（1）解：a与b互为相反数，c与d互为倒数，x的绝对值等于5，
，
当时，；
当时，；
综上所述，的值为或；
（2）解：的立方根是3，的算术平方根是4，
，
，
，
的平方根为，
即的平方根是；
（3）解：在方格中阴影正方形的边长，
，
它的整数部分是3，小数部分是，
故答案为：，3，．
22．（1） （2）x＝0或1时，始终输不出y的值 （3）81
【分析】（1）根据运算的定义即可直接求解；
（2）始终输不出y值，则x的任何次方根都是有理数，则只有0和1；
（3）写出一个无理数，平方是有理数，然后两次平方即可．
【详解】解：(1)由输入x＝25得＝5.因为5是有理数，不能输出，再取5的算术平方根得.因为是无理数，所以输出y，所以输入x＝25时，输出的y的值是.
(2)x＝0或1时，始终输不出y的值．
(3)81(答案不唯一)
【点睛】本题考查无理数，正确理解题目中规定的运算是关键．
23．(1)，理由见解析
(2)
(3)，过程见解析
【分析】（1）根据题干中提供的信息进行解答即可；
（2）根据题目中的式子找出一般规律即可；
（3）将变形为，然后再根据解析（2）中得出的规律进行运算即可．
【详解】（1）解： ；
理由：；
（2）解：；
；
；
……
；
（3）解：
．
【点睛】本题主要考查了二次根式的规律运算，解题的关键是理解题意，熟练掌握二次根式的性质．