

2024年北京师大附属实验中学高考物理零模试卷(含详细答案解析)
展开1.如图所示为斯特林发动机玩具,汽缸在酒精灯加热情况下,汽缸内的活塞往复运动,通过传动轴带动飞轮持续转动,则( )
A. 活塞压缩气体时,气体的压强与体积成反比
B. 气体膨胀时,气体的体积与热力学温度成正比
C. 发动机工作时,气体吸收的热量大于对外做功
D. 气体能从单一热源吸热并全部用来对外做功而不引起其他变化
2.关于光的传播现象及应用,下列说法正确的是( )
A. “3D电影”的播放和观看利用了光的干涉
B. 水中的气泡看起来特别明亮,是因为光从水射向气泡时,一部分光在界面上发生了全反射的缘故
C. 利用电磁波传递信号可以实现无线通信,但电磁波不能通过电缆、光缆传输
D. 一束单色光由空气射入玻璃,这束光的波长变长
3.如图所示,甲为演示光电效应的实验装置;乙图为a、b、c三种光照射下得到的三条电流表与电压表读数之间的关系曲线;丙图为氢原子的能级图;丁图给出了几种金属的逸出功和极限频率关系。以下说法正确的是( )
A. 若b光为绿光,a光可能是紫光
B. 若a光为绿光,c光可能是紫光
C. 若c光光子能量为2.81eV,用它照射由金属铷构成的阴极,所产生的大量具有最大初动能的光电子去撞击大量处于n=3激发态的氢原子,可以产生6种不同频率的光
D. 若c光光子能量为2.81eV,用它直接照射大量处于n=2激发态的氢原子,可以产生6种不同频率的光
4.“战绳”是一种近年流行的健身器材,健身者把两根相同绳子的一端固定在一点,用双手分别握住绳子的另一端,上下抖动绳子使绳子振动起来(图甲)。以手的平衡位置为坐标原点,图乙是健身者右手在抖动绳子过程中某时刻的波形,若右手抖动的频率是0.5Hz,下列说法正确的是( )
A. 该时刻P点的位移为10 3cm
B. 再经过0.25s,P点到达平衡位置
C. 该时刻Q点的振动方向沿y轴负方向
D. 从该时刻开始计时,质点Q的振动方程为y=20sin(πt+π)cm
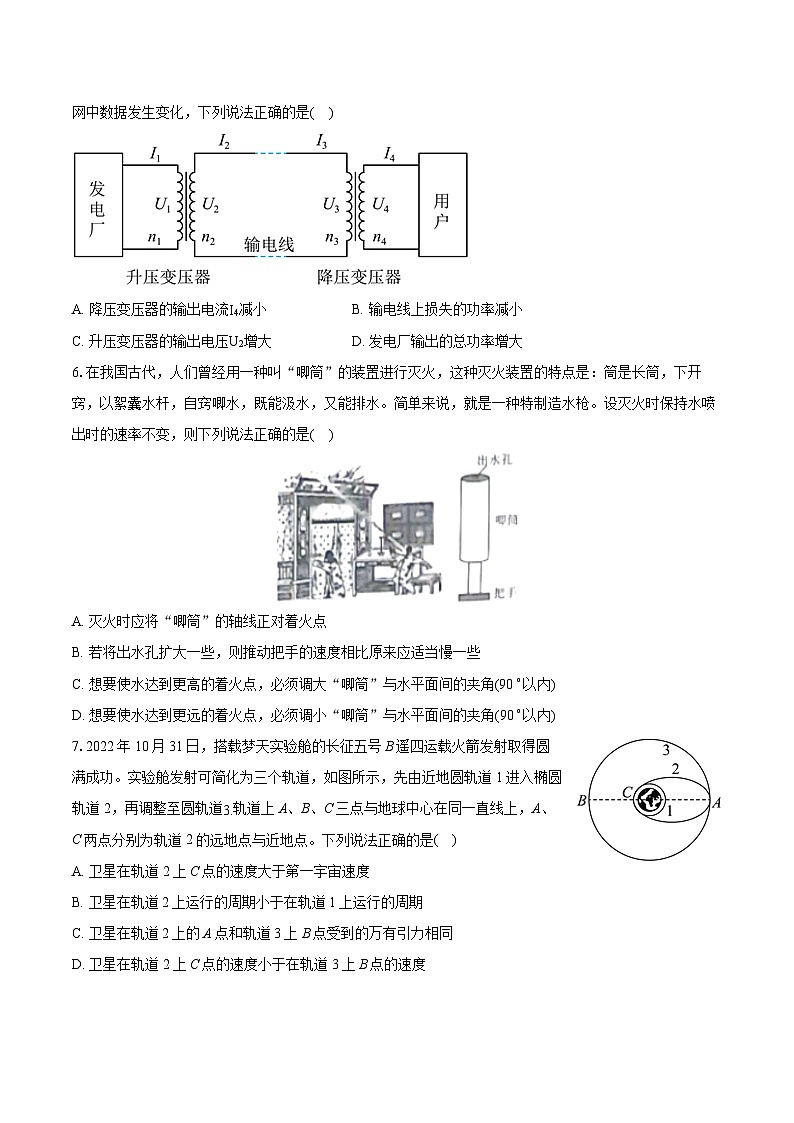
5.随着经济发展,加之寒冬来临,用电需求增加,当火力发电供应紧张时,通过远距离调度方式,会及时将其他地区的风力发电、太阳能发电并入电网保障电力供应。如图是远距离输电的原理图,假设发电厂输出电压恒定不变,两个变压器均为理想变压器。当用户用电器增加(假设所有用电器均可视为纯电阻),电网中数据发生变化,下列说法正确的是( )
A. 降压变压器的输出电流I4减小B. 输电线上损失的功率减小
C. 升压变压器的输出电压U2增大D. 发电厂输出的总功率增大
6.在我国古代,人们曾经用一种叫“唧筒”的装置进行灭火,这种灭火装置的特点是:筒是长筒,下开窍,以絮囊水杆,自窍唧水,既能汲水,又能排水。简单来说,就是一种特制造水枪。设灭火时保持水喷出时的速率不变,则下列说法正确的是( )
A. 灭火时应将“唧筒”的轴线正对着火点
B. 若将出水孔扩大一些,则推动把手的速度相比原来应适当慢一些
C. 想要使水达到更高的着火点,必须调大“唧筒”与水平面间的夹角(90∘以内)
D. 想要使水达到更远的着火点,必须调小“唧筒”与水平面间的夹角(90∘以内)
7.2022年10月31日,搭载梦天实验舱的长征五号B遥四运载火箭发射取得圆满成功。实验舱发射可简化为三个轨道,如图所示,先由近地圆轨道1进入椭圆轨道2,再调整至圆轨道3.轨道上A、B、C三点与地球中心在同一直线上,A、C两点分别为轨道2的远地点与近地点。下列说法正确的是( )
A. 卫星在轨道2上C点的速度大于第一宇宙速度
B. 卫星在轨道2上运行的周期小于在轨道1上运行的周期
C. 卫星在轨道2上的A点和轨道3上B点受到的万有引力相同
D. 卫星在轨道2上C点的速度小于在轨道3上B点的速度
8.如图甲所示,轻杆一端固定在转轴O点,另一端固定一小球,现让小球在竖直平面内做半径为R的圆周运动,小球在最高点受到杆的弹力大小为F,速度大小为v,其F−v2图像如图乙所示,不计空气阻力,则( )
A. v2=b时,杆对小球的弹力方向向上
B. 当地的重力加速度大小为bR
C. 小球的质量为cRa
D. v2=2a时,小球受到的弹力与重力大小不相等
9.如图所示,质量为2000kg的电梯的缆绳发生断裂后向下坠落,电梯刚接触井底缓冲弹簧时的速度为4m/s,缓冲弹簧被压缩2m时电梯停止了运动,下落过程中安全钳总共提供给电梯17000N的滑动摩擦力。已知弹簧的弹性势能为Ep=12kx2(k为弹簧的劲度系数,x为弹簧的形变量),安全钳提供的滑动摩擦力等于最大静摩擦力,重力加速度g=10m/s2,下列说法正确的是( )
A. 弹簧的劲度系数为3000N/m
B. 整个过程中电梯的加速度一直在减小
C. 电梯停止在井底时受到的摩擦力大小为17000N
D. 从电梯接触弹簧到速度最大的过程中电梯和弹簧组成的系统损失的机械能约为4636J
10.地磅工作原理图如图所示,地磅空载时变阻器滑片P位于A点,满载时滑片P位于B点,弹簧始终处于弹性限度内。下列说法错误的是( )
A. 电压表两端电压与被测汽车的质量成正比
B. 若将一个电阻与电压表串联,可增大地磅量程
C. 若称量值偏小,可在R0上并联一个电阻进行校正
D. 电池长时间使用后,称量值会偏小
11.螺旋千斤顶由带手柄的螺杆和底座组成,螺纹与水平面夹角为α,如图所示。水平转动手柄,使螺杆沿底座的螺纹槽(相当于螺母)缓慢旋进而顶起质量为m的重物,如果重物和螺杆可在任意位置保持平衡,称为摩擦自锁。能实现自锁的千斤顶,α的最大值为α0。现用一个倾角为α0的千斤顶将重物缓慢顶起高度h后,向螺纹槽滴入润滑油使其动摩擦因数μ减小,重物回落到起点。假定最大静摩擦力等于滑动摩擦力,不计螺杆和手柄的质量及螺杄与重物间的摩擦力,转动手柄不改变螺纹槽和螺杆之间的压力。下列说法正确的是( )
A. 实现摩擦自锁的条件为tanα≥μ
B. 下落过程中重物对螺杆的压力等于mg
C. 从重物开始升起到最高点摩擦力做功为mgh
D. 从重物开始升起到最高点转动手柄做功为2mgh
12.人体的细胞膜模型图如图a所示,由磷脂双分子层组成,双分子层之间存在电压(医学上称为膜电位),现研究某小块均匀的细胞膜,厚度为d,膜内的电场可看作匀强电场,简化模型如图b所示,初速度可视为零的一价正钾离子仅在电场力的作用下,从图中的A点运动到B点,下列说法正确的是( )
A. 钾离子的电势能增大
B. A点电势等于B点电势
C. 若膜电位增加,则钾离子进入细胞内的速度更大
D. 若膜电位不变,膜的厚度越大,则钾离子进入细胞内的速度越大
13.如图甲所示,两间距为L的平行光滑金属导轨固定在水平面内,左端用导线连接,导轨处在竖直向上的匀强磁场中,一根长度也为L、电阻为R的金属棒放在导轨上,在平行于导轨向右、大小为F的恒力作用下向右运动,金属棒运动过程中,始终与导轨垂直并接触良好,金属棒运动的加速度与速度关系如图乙所示,不计金属导轨及左边导线电阻,金属导轨足够长,若图乙中的a0、v0均为已知量,则下列说法不正确的是( )
A. 金属棒的质量为Fa0
B. 匀强磁场的磁感应强度大小为1L FRv0
C. 当拉力F做功为W时,通过金属棒横截面的电荷量为W FR
D. 某时刻撤去拉力,此后金属棒运动过程中加速度大小与速度大小成正比
14.地球半径约为6400km,地球表面的大气随海拔高度增加而变薄,大气压强也随之减小到零,海拔100km的高度被定义为卡门线,为大气层与太空的分界线。有人设想给太空飞船安装“太阳帆”,用太阳光的“光子流”为飞船提供动力来实现星际旅行。已知在卡门线附近,一个正对太阳光、面积为1.0×106m2的平整光亮表面,受到光的压力约为9N;力虽小,但假设以同样材料做成面积为1.0×104m2的“帆”安装在飞船上,若只在光压作用下,从卡门线附近出发,一个月后飞船的速度可达到2倍声速。设想实际中有一艘安装了“帆”(面积为1.0×104m2)的飞船,在卡门线上正对太阳光,下列说法正确的是( )
A. 飞船无需其他动力,即可不断远离太阳
B. 一年后,飞船的速度将达到24倍声速
C. 与太阳中心的距离为日地间距离2倍时,“帆”上的压力约为2.25×10−2N
D. 与太阳中心的距离为日地间距离2倍时,飞船的加速度为出发时的14
二、实验题:本大题共2小题,共18分。
15.用图1所示装置探究气体等温变化的规律。
(1)①实验中,为找到体积与压强的关系,______(选填“需要”或“不需要”)测量空气柱的横截面积;
②关于该实验的操作,下列说法正确的有______;
A.柱塞上应该涂油
B.应缓慢推拉柱塞
C.用手握住注射器推拉柱塞
D.注射器必须固定在竖直平面内
(2)①如图2所示,在“用双缝干涉测量光的波长”实验某次测量中,将测量头的分划板中心刻线与某条亮条纹中心对齐,将该亮条纹记为第1条亮条纹,此时手轮上的示数如图2甲所示。然后同方向转动测量头,使分划板中心刻线与第6条亮条纹中心对齐,此时手轮上的示数如图2乙所示,则此示数为______ mm,由此可求得相邻亮条纹的间距Δx为______ mm。
②已知双缝间距d为2.0×10−4m,测得双缝到屏的距离l为0.700m,由计算式λ=______,求得所测红光波长为______ nm。
(3)某同学利用多用电表的欧姆挡进行实验研究。欧姆挡所用电池的电动势为9V,刻度盘中央刻度值为“15”,选择旋钮打在“×1k”挡。该同学用欧姆挡测量某一量程为15V的电压表内阻。
①指针指在图3甲所示位置,此测量值为______kΩ;查阅资料发现该电压表内阻真实值为15kΩ,测量值与真实值偏差较大,可能原因是该同学未进行欧姆调零就直接测量,若此时把两表笔短接,则指针应指在欧姆挡零刻度线的______侧(选填“左”或“右”)。
②进行欧姆调零后再测量,多用电表指针恰好指在“15”刻度线,此时电压表示数为______V(结果保留2位有效数字)。
16.为了探究平抛运动的规律,某同学用如图(a)所示的装置进行实验。
(1)为了准确地描绘出平抛运动的轨迹,下列要求合理的是______。
A.小球每次必须从斜槽上同一位置由静止释放
B.斜槽轨道必须光滑
C.斜槽轨道末端必须水平
D.本实验必需的器材还有刻度尺和停表
(2)甲同学按正确的操作完成实验并描绘出平抛运动的轨迹,以平抛运动的初始位置O为坐标原点建立xOy坐标系,如图(b)所示。从运动轨迹上选取多个点,根据其坐标值可以验证轨迹符合y=ax2的抛物线。若坐标纸中每个小方格的边长为L,根据图中M点的坐标值,可以求出a=______,小球平抛运动的初速度v0=______。(重力加速度为g)
(3)乙同学不小心将记录实验的坐标纸弄破损,导致平抛运动的初始位置缺失。他选取轨迹中任意一点O为坐标原点,建立xOy坐标系(x轴沿水平方向、y轴沿竖直方向),如图(c)所示。在轨迹中选取A、B两点,坐标纸中每个小方格的边长仍为L,重力加速度为g。由此可知:小球从O点运动到A点所用时间t1与从A点运动到B点所用时间t2的大小关系为:t1______t2(选填“>”“<”或“=”);小球平抛运动的初速度v0=______,小球平抛运动的初始位置坐标为(______,______)。
(4)丙同学将实验方案做了改变,如图(d)所示,他把桌子搬到竖直墙的附近,调整好仪器,使从斜槽轨道滚下的小球打在正对的墙上,把白纸和复写纸附在墙上,记录小球的落点。然后等间距地改变桌子与墙的距离,就可以得到多个落点。如果丙同学还有一把刻度尺,他是否可以计算出小球平抛时的初速度?并简要阐述由。______。
三、简答题:本大题共3小题,共30分。
17.跳楼机可以使人体验失重和超重(如图所示)。现让升降机将座舱送到距地面H=78m的高处,然后让座舱自由下落,落到距地面h=30m的位置时开始制动,使座舱均匀减速,座舱落到地面时刚好停下。在该体验中,小明将质量m=10kg的书包平放在大腿上(不计空气阻力,g取10m/s2)。求:
(1)当座舱落到距地面h1=50m的位置时,小明对书包的作用力大小F1;
(2)跳楼机制动后(匀减速阶段)加速度a的大小;
(3)当座舱落到距地面h2=15m的位置时,小明对书包的作用力大小F2。
18.如图a所示,真空室中电极K发出的电子(初速为零,不计重力)。经U0的加速电场后,由小孔S沿两水平金属板A、B两板间的中心线射入,A、B板长l,相距d,加在A、B两板间的电压U随时间t变化U−t图线如图b。设A、B两板间的电场可以看作是均匀的,且两板外无电场。在每个电子通过电场区域的极短时间内,电场可视作恒定的。两板右侧放一记录圆筒,筒的左侧边缘与极板右端距离为b,筒绕其竖直轴以周期T做匀速转动,筒的周长s,筒能接收到通过A、B板的全部电子。
(1)要求任意时刻入射的电子均能从极板间出射,则对于U0有何要求?
(2)在(1)问条件下(下同),以t=0时刻发射的电子(见图b,此时U=0)打到圆筒记录纸上的点作xOy坐标系的原点,并取y轴竖直向上,试计算电子打到记录纸上的最高点的x坐标和y坐标;并在图d给出的坐标纸上定性地画出电子打到记录纸上的点形成的图线(在坐标轴上标出关键点)。
(3)若把记录圆筒放到B板的右上方,如图c所示,设偏转电场的中轴线与圆筒的最高点距离为H。加速电压U0不变,若t时刻发射出的电子打到滚筒上面的点到极板右侧的距离为c。
a.试证明c与1t的图像在0
19.阿特伍德机是由英国物理学家乔治⋅阿特伍德在1784年发表的《关于物体的直线运动和转动》一文中提出的,用于测量加速度及验证运动定律的机械。如图所示,一定滑轮两端分别与质量为3m的物体A和质量为m的物体B相连。不计轮轴间的摩擦力和空气阻力,假设绳子与轮轴间不会打滑。
(1)若不计滑轮质量,两物体均由静止释放,试求物体A下落高度h后,两物体的速度大小。
(2)类比是一种常见的解决物理问题的方式。若滑轮的质量不可忽略,由于其自身惯性的存在,其角速度增加的过程也会受到阻碍。因此我们可以用转动惯量I作为其转动过程中惯性大小的量度,用角加速度α描述其转动加快过程中角速度的变化率。
a.在把物体视为质点时,我们可以利用牛顿第二定律描述合力与加速度的关系。类比这种关系,在刚体(形变可忽略的物体)的转动过程中,我们同样可以用类似的关系描述刚体的合力矩M(力矩是矢量,大小等于物体某点所受的力与其力臂的乘积,以使物体逆时针旋转的力矩方向为正方向)与角加速度(角速度的变化率)的关系。请根据角加速度的定义,类比线速度与角速度的关系,直接写出角加速度与半径为r的圆盘边缘的线加速度a的关系,并类比质点的牛顿第二定律,直接写出刚体转动过程中合力矩、转动惯量和角加速度的关系。
b.在把系统内各物体都视为质点时,我们可以利用机械能守恒描述物体重力势能与动能的相互转化。若考虑到刚体的转动动能,我们在使用机械能守恒的过程中,动能除了我们熟知的质点的平动动能以外,还需要加上有质量的刚体的转动动能。试类比质点的平动动能,写出刚体转动角速度为ω时刚体的转动动能Ek转。
c.若滑轮的质量为m,半径为R,其转动惯量的表达式I=12mR2。请根据以上关系,求解考虑滑轮质量的前提下,与物体A相连的轻绳拉力大小T1,与物体B相连的轻绳拉力大小T2,以及物体A下落高度h后的速度大小。
四、计算题:本大题共1小题,共10分。
20.世界多国都在加紧研制真空管道高速磁悬浮列车某研发团队想要探究其电磁刹车的效果。在遥控小车底面安装N正方形线框abcd,边长为L,线框总电阻为R,其平面与水平轨道平行,小车总质量为m,其俯视图如图所示。小车到站需要减速时,在前方虚线PP′和QQ′之间设置一竖直向上的匀强磁场,磁感应强为B,宽度为H,且H>L.若小车关闭引擎即将进入磁场前的速度为v0,在行驶过程中小车受到轨道阻力可忽略不计,不考虑车身其他金属部分的电磁感应现象。求:
(1)cd边刚进入磁场时线框内感应电流的大小和方向:
(2)cd边刚进入磁场时,小车的加速度大小:
(3)若小车完全进入磁场时速度为v02,求在此过程中通过线圈的电荷量和线圈产生的焦耳热。
答案和解析
1.【答案】C
【解析】解:A.可把汽缸内的气体看成理想气体,当活塞压缩气体时,气体温度要发生变化,根据一定质量的理想气体的状态方程pVT=C可知,只有当气体的温度不变时,气体的压强才与体积成反比,故A错误;
B.气体膨胀时,气体压强要发生变化,根据一定质量的理想气体的状态方程pVT=C可知,只有当气体的压强不变时,气体的体积才与热力学温度才成正比,故B错误;
C.发动机工作时,气体从外界吸收热量温度升高,内能增加,且气体同时对外做功,根据热力学第一定律ΔU=Q+W,可知吸收的热量大于对外做的功,故C正确;
D.根据热力学第二定律可知,气体不可能从单一热源吸热并全部用来对外做功而不引起其他变化,故D错误。
故选:C。
根据一定质量的理想气体的状态方程分析出气体状态参量之间的关系;
根据热力学第一定律分析出气体吸收的热量与做功的大小关系;
根据热力学第二定律的概念结合题意完成分析。
本题主要考查了一定质量的理想气体的状态方程,结合热力学定律即可完成分析。
2.【答案】B
【解析】解:A、“3D电影”的播放和观看利用了光的偏振现象,故A错误;
B、水中的气泡看起来特别明亮,是因为光从水射向气泡时,即从光密质射向光疏介质时,一部分光在界面上发生了全反射,故B正确;
C、电磁波可以在真空中传播,也可以在光导纤维中传播,故C错误;
D、光由空气射入玻璃,光速变小,所以波长变小,故D错误。
故选:B。
“3D电影”的播放和观看利用了光的偏振;水中的气泡看起来特别明亮是全反射;电磁波可以在真空中传播,也可以在其他介质中传播;根据波速公式判断。
本题考查了光的偏振现象、全反射、电磁波的传播应用等光学的相关问题,考查知识点针对性强,难度较小,考查了学生掌握知识与应用知识的能力。
3.【答案】C
【解析】解:AB、由光电效应方程:Ek=hν−W0及eUc=Ek,联立解得:eUc=hν−W0。即光束照射同一块金属的时候,只要遏止电压一样,说明入射光的频率一样,遏止电压越大,入射光的频率越大,因此可知a光和c光的频率一样,且均小于b光的频率,故若b光为绿光,a光不可能是紫光,故AB错误;
C、若b光光子能量为2.81ev,用它照射由金属铷构成的阴极,所产生的大量具有最大初动能的光电子的最大初动能:Ekm=2.81eV−2.13eV=0.68eV。
去撞击大量处于n=3激发态的氢原子时,能量值最大可以达到:E=Ekm+E3=0.68eV−1.51eV=−0.83eV。由于该能量值介于氢原子的第4能级与第5能级之间,可知该光电子与氢原子碰撞,可以使氢原子吸收0.66eV的能量跃迁到n=4的能级。
当大量的处于n=4能级的氢原子向低能级跃迁时,可以产生C42=6种不同频率的光,故C正确;
D、若b光光子能量为2.81ev,用它直接照射大量处于n=2激发态的氢原子,能量值最大可以达到:E=Ekm+E2=0.68eV−3.4eV=−2.72eV。由于该能量值介于氢原子的第2能级与第3能级之间,可知该光电子与氢原子碰撞,氢原子不能吸收0.68eV的能量发生跃迁,故D错误。
故选:C。
根据遏止电压比较最大初动能,从而比较光子频率的大小,得出可能的情况;结合玻尔理论,由能级之间的关系判断。
解决本题的突破口在于通过遏止电压比较最大初动能,结合光电效应方程进行分析。
4.【答案】B
【解析】解:ABC.由题可知,振幅A=20cm,频率f=0.5Hz,由图可知波的波长为λ=8m,波向右传播,该时刻P点得振动方向沿y轴负方向,O点的振动方向沿y轴正方向,故从该时刻开始计时P点的振动方程为y=20sin(πt+3π4)cm
故t=0时P点的位移为y=10 2cm
当t=0.25s时P点的位移为y=0,P点到达平衡位置,故AC错误,B正确;
D.从该时刻开始计时,质点O从平衡位置向上振动,故质点Q的振动方程为y=20sin(πt)cm,故D错误。
故选:B。
根据波形平移法分析Q的运动方向;根据振幅、频率可得该时刻开始计时PQ点的振动方程,从而分析P的位移和运动情况。
解决本题的关键是要会用波形平移法分析质点的起振方向,注意质点振动方程的书写。
5.【答案】D
【解析】解:C、根据原、副线圈电压比等于匝数比可得U1U2=n1n2
可得升压变压器的输出电压为U2=n2n1U1
由于匝数不变,发电厂输出电压恒定不变,可知升压变压器的输出电压U2不变,故C错误;
A、原副线圈电压比等于匝数比,电流比等于匝数反比,设输电线电阻为R线,用户端总电阻为R,在高压传输电路上,有U2=U3+I2R线
又U3U4=n3n4
I2I4=n4n3
I4=U4R
联立可得:U2=(n3n4R+n4n3R线)I4
当用户用电器增加,用电器为并联,用户端总电阻R减小,则降压变压器的输出电流I4增大,故A错误;
B、原副线圈电流比等于匝数的反比,有:I2I4=n4n3
由A得,I4增大,则I2增大,输电线上损失的功率为P损=I22R线
输电线上损失的功率增大,故B错误;
D、根据I1I2=n2n1
由B得,I2增大,则I1增大,发电厂输出的总功率为P出=U1I1
发电厂输出的总功率增大,故D正确。
故选:D。
变压器原副线圈电压比等于匝数比,电流比等于匝数反比,据此判断电压和电流的变化;根据功率公式求解输电线上损失的功率,进而判断功率的变化;根据P=UI判断发电机输出总功率的变化。
本题考查远距离输电问题,解题关键是知道变压器原副线圈电压比、电流比与匝数比的关系,掌握功率的计算公式。
6.【答案】C
【解析】解:A、水离开出水口后做抛体运动,所以灭火时不能将“唧筒”的轴线指向着火点,故A错误;
B、若将出水孔扩大一些,则推动把手的速度相比原来应适当快一些,才能使水喷出的速度大小不变,故B错误。
C、当调大“唧筒”与水平面间的夹角,即水在竖直方向的初速度增大,所以竖直位移更大,将到达更高的着火点,故C正确;
D、当调小“唧筒”与水平面间的夹角时,水在空中的时间减小,虽然水在水平方向的速度增大,但是不一定能使水达到更远的着火点,故D错误。
故选:C。
由题意,用“唧筒”装置进行灭火,实际是一个斜抛问题,运用斜抛运动的知识进行分析。
本题主要考查斜抛运动的应用,难度较小。
7.【答案】A
【解析】解:A、轨道1为近地圆轨道,卫星运行的速度为第一宇宙速度,卫星由1轨道变到2轨道,要做离心运动,因此在C点应该加速,所以在2轨道上C点的速度大于1轨道上C点的速度,即卫星在轨道2上C点的速度大于第一宇宙速度,故A正确;
C、根据万有引力公式:F=GMmr2,可知卫星在轨道2上的A点和轨道3上B点受到的万有引力大小相同,方向不同,故C错误;
B、根据开普勒第三定律:R3T2=k,可知轨道半径越大,周期越大,所以卫星在轨道2上运行的周期大于在轨道1上运行的周期,故B错误;
D、根据万有引力提供向心力:GMmr2=mv2r,解得:v= GMr,可知卫星在1轨道上运行的速度大于卫星在3轨道上的速度,而卫星在轨道2上C点的速度大于卫星在轨道1上C点的速度,所以卫星在轨道2上C点的速度大于在轨道3上B点的速度,故D错误。
故选:A。
根据航天器从轨道1到轨道2需要做离心运动,则航天器要加速,判断卫星在两轨道上经过C点的速度大小;
根据万有引力的方向确定卫星在两点的万有引力是否相同;
由开普勒第三定律分析轨道1和2的周期关系;
根据万有引力提供向心力,获得线速度公式,从而比较卫星在不同轨道上不同点的线速度大小。
本题关键是明确加速度由合力和质量决定,导致同一位置的卫星的加速度相同;然后结合开普勒第三定律和牛顿第二定律列式分析。
8.【答案】C
【解析】解:A、当v2=a时,杆子的弹力为零,v2=b时,杆子出现拉力,杆对小球的弹力方向向下,故A错误;
B、当v2=a时,杆子的弹力为零,有:mg=mv2R,解得:g=aR,故B错误;
C、当小球的速度为零时,F=c,则有:F=mg=c,解得小球的质量为m=cRa,故C正确;
D、当v2=2a时,根据牛顿第二定律得,F+mg=mv2R,又由于g=aR,解得:F=mg,故D错误。
故选:C。
根据v2=a时,F=0,靠重力提供向心力,结合牛顿第二定律求出v2=b时杆子作用力的方向;根据牛顿第二定律求出当地的重力加速度;根据v=0时,F=c,得出小球的质量;当v2=2b时,根据牛顿第二定律分析小球的重力与杆子弹力大小的关系。
本题主要考查了圆周运动向心力公式的直接应用,要求同学们能根据图象获取有效信息,难度适中。
9.【答案】D
【解析】解:A.电梯刚接触井底缓冲弹簧时的速度为4m/s,缓冲弹簧被压缩2m时电梯停止了运动,根据能量守恒定律有
12mv2+mg⋅Δx=12k⋅Δx2+f动⋅Δx
代入数据解得
k=11000N/m,故A错误;
B.与弹簧接触前,电梯做匀加速直线运动,接触弹簧后,先做加速度逐渐减小的加速运动后做加速度逐渐增加的减速运动,故B错误;
C.电梯停止在井底时,由受力平衡得
kΔx=mg+f静
代入数据解得
f静=kΔx−mg=11000×2N−2000×10N=2000N,故C错误;
D.当电梯速度最大时,此时加速度为零,则
kΔx′+f动=mg
代入数据解得
Δx′=311m
电梯接触弹簧到速度最大的过程中,电梯和弹簧组成的系统损失的机械能等于摩擦力做的负功,则
ΔE=f动⋅Δx′=17000×311J≈4636J,故D正确。
故选:D。
A:根据能量守恒定律求解弹簧的劲度系数;
B:根据电梯的运动性质判断;
C:根据平衡条件求解电梯停止在井底时受到的摩擦力大小;
D:先根据速度最大时合力为零求解弹簧的压缩量,再根据功能关系求解该过程中电梯和弹簧组成的系统损失的机械能。
本题考查功能关系,要求学生能正确分析物体的运动过程和运动性质,熟练应用对应的规律解题。
10.【答案】B
【解析】解:A、设变阻器AB的总电阻为R,横截面积为S,根据闭合电路欧姆定律得:
E=I(R+R0+r)
设AP之间的距离为x,由欧姆定律得:
U=IRx=ER+R0+r⋅ρxS
汽车平衡时,由平衡条件得mg=2kx
联立解得:U=ER+R0+r⋅mgρ2kS
从公式可以看出:电压表两端电压U与被测汽车的质量m成正比,故A正确;
B、若将一个电阻与电压表串联,AP之间的最大电压不受此电阻的影响,没有办法增大地磅量程,故B错误;
C、若称量值偏小,可以通过在R0上并联一个电阻,回路中总电阻变小,总电流增大,可变电阻上的电压增大,使称量值不变,故C正确;
D、电池长时间使用后,内阻会变大,导致电流减小,AP上的电压减小,所以称量值会偏小,故D正确。
本题选错误的,
故选:B。
根据闭合电路欧姆定律、欧姆定律和胡克定律相结合得出电压表两端电压与被测汽车的质量关系式,再分析它们的关系。若将一个电阻与电压表串联,AP之间的最大电压不受此电阻的影响,对地磅量程没有影响。若称量值偏小,根据欧姆定律分析校正方法。电池长时间使用后,根据电压表达式分析称量值的变化。
本题综合考查闭合电路欧姆定律及胡克定律等有关知识,要注意寻找题目中的隐含条件,建立各知识点间的联系。
11.【答案】D
【解析】解:A、实现自锁的条件是重物重力沿斜面下滑的分力小于等于最大静摩擦力,即mgsinα≤μmgcsα,解得μ≥tana,故A错误;
B、重物从静止开始下落,说明开始螺杆对重物的支持力小于mg,加速下滑过程中,螺杆对重物的支持力小于mg,最后重物的速度为零,说明最后有一段减速下滑的过程,此过程中重物属于超重,螺杆对重物的支持力大于mg,根据牛顿第三定律可知重物对螺杆的作用力先小于mg,后大于mg,故B错误:
C、由于千斤顶的倾角为α0,所以重物在上升过程中受到的摩擦力为f=mgsinα0,设螺纹的总长度为L,则摩擦力做的功为:Wf=−fL=−mgLsinα0,而Lsinα0=h,所以摩擦力做的功为Wf=−mgh,故C错误;
D、设从重物开始升起到最高点转动手柄做的功为W,根据动能定理可得:W+Wf−mgh=0,解得:W=2mgh,故D正确。
故选:D。
根据实现自锁的条件列方程求解;根据重物下落过程中的运动情况分析受力情况,再根据牛顿第三定律可知重物对螺杆的作用力的变化情况:根据平衡条件求解摩擦力的大小,根据摩擦力做功的计算公式求解摩擦力做的功;根据动能定理求解从重物开始升起到最高点转动手柄做的功。
本题主要是考查了功能关系和能量守恒定律,首先要选取研究过程,分析运动过程中物体的受力情况和能量转化情况,然后分析运动过程中哪些力做正功、哪些力做负功,初末动能为多少,根据功能关系列方程解答。
12.【答案】C
【解析】解:A.初速度可视为零的一价正钾离子仅在电场力的作用下,从图中的A点运动到B点,则电场力从A指向B,可知钾离子运动中电场力做正功,所以钾离子的电势能减小,故A错误;
B.初速度可视为零的一价正钾离子仅在电场力的作用下,从图中的A点运动到B点,则电场力从A指向B,故电场线从A到B,沿电场线电势降低,所以A点电势大于B点电势,故B错误;
CD.由动能定理知qU=12mv2可知:
若膜电位增加,即电压U增加时,速度增大,膜电位不变时,即电压U不变时,钠钾子进入细胞内的速度不变;两者均与膜的厚度无关,故C正确,D错误。
故选:C。
根据题意可知电场线方向,沿电场线方向电势逐渐降低,电场力做正功,电势能减小,根据动能定理分析速度的变化。
本题考查电势能与电场力做功,解题关键掌握电场线的特点,注意沿电场线方向电势逐渐降低。
13.【答案】C
【解析】解:AB、金属棒向右运动切割磁感线的过程中,由E=BLv,I=ER,F安=BIL,可得:F安=B2L2vR
根据牛顿第二定律得:F−F安=ma,联立可得:a=Fm−B2L2mRv
根据图乙的加速度与速度关系可得:Fm=a0;B2L2mR=a0v0
解得金属棒的质量m为Fa0,磁感应强度B的大小为1L FRv0,故AB正确;
C、当拉力F做功为W时,根据W=Fx,可得金属棒的位移x=WF
通过金属棒横截面的电荷量q=I−t=E−Rt=ΔΦR=BLxR,联立可得:q=W FRv0,故C错误;
D、某时刻撤去拉力,根据牛顿第二定律得:F安=ma′,可得:B2L2vR=ma′,可知此后金属棒运动过程中加速度大小与速度大小成正比,故D正确。
本题选择错误的选项,故选:C。
根据法拉第电磁感应定律,闭合电路欧姆定律,安培力计算公式,应用牛顿第二定律推导出加速度与速度关系式,结合图像的斜率与截距求解金属棒的质量和磁感应强度的大小;根据拉力F做的功得到金属棒的位移,根据通过金属棒横截面的电荷量的经验公式求解;根据牛顿第二定律解答撤去拉力后金属棒运动过程中加速度大小与速度大小的关系。
本题考查了电磁感应的力学问题,研究思路常常有两条:一条从力的角度,重点是分析安培力作用下导体棒的运动过程,根据平衡条件、牛顿第二定律、动量定理列出方程;另一条是能量,分析涉及电磁感应现象中的能量转化问题,根据动能定理、功能关系等列方程求解。
14.【答案】C
【解析】A、设太阳帆距太阳的距离为r,太阳单位时间发出的光子数为N,一个光子对太阳帆的作用力为F0,则光压F=N×S4πr2×F0,因为当S=1.0×106m2的时候,光压F=9N,则当面积是S′=1.0×104m2的时候,光压F',则存在FS=F′S′,解得F′=9×10−2N;当S=1.0×104m2的帆能远离太阳运动时,说明光压大于万有引力,即N×S4πr2×F0>GMmr2,两边约掉r2,说明当r增大时光压仍大于太阳对它的万有引力,但是太阳帆在远离太阳的过程中,可能还会遇到其他的星体,所以还可能受到其他星体的作用力从而不能不断远离太阳,故A错误;
B、已知一个月后飞船的速度可达到2倍声速,则如果飞船的加速度始终和第一个月的加速度相同,那么12个月(一年)后的速度将达到:2倍声速×12=24倍声速,但由于太阳帆在远离太阳的过程中,其光压随距离的平方的增大而减小,所以太阳帆做的是加速度减小的加速运动,故一年后,飞船的速度达不到24倍声速,故B错误;
C、根据F与r2成反比可知,当与太阳中心的距离为日地间距离2倍时,“帆”上的压力变为原来的14,即9×10−2N×14=2.25×10−2N,故C正确;
D、如果只考虑太阳对太阳帆的作用力,根据F=ma,由于力减小为原来的14,则飞船的加速度也会变为原来的14,但飞船在飞行的过程中还受到其他星体的万有引力,所以加速度不一定是原来的14,故D错误。
故选:C。
根据对飞船受力分析情况判断飞船运动状态,即比较飞船受到的万有引力及飞船上“太阳帆”的光压力大小;根据飞船受力对飞船运动状况进行判断,从而分析出一年后的飞船速度;根据“帆”上的压力与距离的关系进行求解;根据飞船受力结合牛顿第二定律分析加速度。
本题题目综合程度较高,题目考查背景比较新颖,解题关键是需要明确太阳帆上受力情况,综合应用万有引力定律及牛顿运动定律解决。
15.【答案】不需要 Δxdl 660 25 左侧 4.5
【解析】解:(1)①由于注射器的横截面积相等,所以在此可用长度代替体积,故不需要测空气柱的横截面积;
②A.柱塞上涂油,既减小摩擦,又防止漏气,故A正确;
B.若急速推拉活塞,则有可能造成漏和等温条件的不满足,所以应缓慢推拉活塞,故B正确;
C.手握活塞造成温度变化,故C错误;
D.压强由压力表测量,不是由竖直的平衡条件计算,所以不需要竖直放置,故D错误;
故选:AB。
(2)①图甲读数为:x1=2mm+32.0×0.01mm=2.320mm,图乙中手轮上的示数:x6=13.5mm+37.0×0.01mm=13.870mm,相邻亮条纹的间距:Δx=x6−x15=2.310mm,
②由Δx=ldλ可得:λ=Δxdl,代入数值可得所测光波长:λ=2.310×10−3×2.0×10−40.700m=6.6×10−7m=660nm。
(3)①选择旋钮打在“×Ik”挡,指针指在图甲所示位置,此测量值为:25×lkΩ=25kΩ,查阅资料发现该电压表内阻真实值为15kΩ,测量值与真实值偏差较大,可能原因是该同学未进行欧姆调零就直接测量,则多用电表内阻偏大,若此时把两表笔短接,可知电流为达到满偏电流,则指针应指在欧姆挡零刻度线的左侧。
②进行欧姆调零后再测量,多用电表指针恰好指在“15”刻度线,此时电流为满偏电流的一半,即电压表的内阻等于欧姆表调零后的内阻,则此时电压表示数为欧姆表内电源电动势的一半,即4.5V。
故答案为:(1)①不需要②AB。
(2)①13.870;2.310②Δxdl;660。
(3)①25;左②4.5。
(1)验证理想气体体积与压强的关系,实验前在柱塞上涂好润滑油,以免漏气,(改变气体体积时,缓慢进行,等稳定后再读出气体压强,以防止气体体积变化太快,气体的温度发生变化实验过程中,不用手接触注射器的圆筒,防止圆筒从手上吸收热量,引起内部气体温度变化。
(2)根据螺旋测微器读数方法读出第一条亮纹和第六条亮纹的数据,求得亮纹的宽度,根据Δx=dLλ求解波长。
(3)根据欧姆表读数方法读取数据,再乘以挡位得到电压表内阻,根据多用电表原理分析并计算。
本题主要考查探究气体等温变化的规律、“用双缝干涉测量光的波长”实验和利用多用电表的欧姆挡进行实验研究,理解熟悉各实验原理是解题关键。
16.【答案】AC15L 5gL2 = 8gL −4L−L可以,理由见解析
【解析】解:(1)AB.斜槽轨道不必光滑,只要小球每次从斜槽上同一位置由静止释放,确保小球做平抛运动的初速度相同即可,故B错误,A正确;
C.斜槽轨道末端必须水平,小球才能水平飞出做平抛运动,故C正确;
D.本实验必需的器材还有刻度尺,不需要秒表,故D错误。
故选:AC。
(2)轨迹符合y=ax2的抛物线,则
a=yx2=5L(5L)2=15L
根据平抛运动规律得,
水平方向上:5L=v0t
在竖直方向上:5L=12gt2
联立解得:v0= 5gL2
(3)水平方向做匀速运动,小球从O点运动到A点所用时间为
t1=4Lv0
从A点运动到B点所用时间为
t2=4Lv0=t1
根据
y2−y1=gΔt2
可得
Δt= 2Lg
小球平抛运动的初速度为
v0= 8gL
小球在A点竖直方向的速度为
vy=3L+5L2Δt
小球平抛运动的初始位置到4点的时间为
t′=vyg
小球平抛运动的初始位置到A点的竖直位移为
y=12gt′2
x=v0t′
解得y=4L,x=8L.
小球平抛运动的初始位置坐标为(−4L,−L)
(4)可以计算小球平抛运动的初速度,用刻度尺测量落点与抛出点之间的竖直距离y,测量墙与桌子的水平距离x,根据y=12gt2
可得t= 2yg
初速度v0=xt=x g2y
所以改变桌子与墙的水平距离x,测量多组x,y值,计算多组初速度,取平均值即可。
故答案为:(1)AC;(2)15L; 5gL2;(3)=; 8gL;−4L;−L;(4)可以,理由见解析
(1)根据实验的原理以及操作中的注意事项确定正确的操作步骤;
(2)根据数学方法结合平抛运动规律解答;
(3)平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动,根据水平位移得出时间的表达式,结合位移-时间公式,抓住竖直位移之差求出小球的初速度,同时计算初始位置的坐标;
(4)根据平抛运动规律分析解答。
解决本题的关键知道实验的原理和注意事项,知道平抛运动在水平方向和竖直方向上的运动规律,结合运动学公式和推论灵活求解。
17.【答案】解:(1)座舱自由下落到距地面h=30m的位置时开始制动,所以当座舱距地面h1=50m时,仍在自由下落,书包处于完全失重状态,则F1=0。
(2)座舱自由下落高度为
H−h=78m−30m=48m
设座舱开始制动时,已获得速度vm,由运动学公式得
vm2=2g(H−h)
座舱制动过程做匀减速直线运动,则有
vm2=2ah
联立可得:a=16m/s2,方向竖直向上,
即跳楼机制动后(匀减速阶段)加速度a的大小为16m/s2。
(3)当座舱落到距地面h2=15m的位置时,对书包,由牛顿第二定律得
F2−mg=ma
代入数据得F2=260N
即当座舱落到距地面h2=15m的位置时,小明对书包的作用力大小为260N。
答:(1)当座舱落到距地面h1=50m的位置时,小明对书包的作用力大小F1为0;
(2)跳楼机制动后(匀减速阶段)加速度a的大小为16m/s2;
(3)当座舱落到距地面h2=15m的位置时,小明对书包的作用力大小为260N。
【解析】(1)不计空气阻力,让座舱自由下落,书包处于完全失重状态,小明对书包的作用力为0。
(2)根据速度-位移公式求出座舱落到距地面h=30m的位置时速度,并由速度-位移公式求出座舱制动过程的加速度大小。
(3)对书包,由牛顿第二定律计算小明对书包的作用力大小F2。
本题的关键要明确书包的运动状态,正确分析书包的受力情况,搞清跳楼机的运动过程,根据牛顿第二定律和运动学公式综合计算。
18.【答案】解:(1)电子在电场中加速,根据动能定理有
eU0=12mv02
电子进入金属板A、B两板间做类平抛运动,根据运动学公式,水平方向的匀速直线运动有
l=v0t
竖直方向的匀加速直线运动有
y≤12at2=d2
竖直方向根据牛顿第二定律有
eUmd=ma
联立解得
U0≥Uml22d2;
(2)电子在A、B两板间竖直方向做出速度为0的匀加速直线运动,根据运动学公式,A、B板间竖直方向的位移为
y=12at2=12×eUmmd×(l 2eU0m)2=Uml24U0d
根据几何关系,平抛运动速度角与位移角关系
yY=l2l2+b
联立解得
Y=Uml(l+2b)4U0d
根据运动学公式,圆筒上有
x=v⋅T2=sT⋅T2=s2
做出的图像如图所示
;
(3)a.根据第(2)求解y坐标有
H=Ul(l+2c)4U0d
解得
c=2U0dHUl−l2
半个周期内电压与时间的关系式为
U=Um0.5T⋅t
联立解得
c=U0dHTUml⋅1t−l2;
b.又上式可知,c−1t的函数斜率为
k=U0dHTUml
解得
H=kUmlU0dT。
答:(1)要求任意时刻入射的电子均能从极板间出射,则对于U0应满足的条件为U0≥Uml2d2;
(2)电子打到记录纸上的最高点的x坐标为s2和y坐标为Uml(l+2b)4U0d;图像如图所示
;
(3)a.证明如上,该函数的解析式为c=U0dHTUml⋅1t−l2。
b.若已知c−1t的函数斜率为k,偏转电场的中轴线距离圆筒的最高点距离H的大小为kUmlU0dT。
【解析】(1)根据动能定理求解电子从加速电场中出来的速度,根据牛顿第二定律求解电子在偏转电场中运动的加速度,再根据运动学公式列式,联立求解加速电压;
(2)根据运动学公式求解电子在A、B两板间的偏转位移,再根据几何关系求解电子电子打到记录纸上的最高点的y坐标,根据运动学公式求解电子打到记录纸上的最高点的x坐标,根据电压图像可知,y坐标呈现行变化,据此作出图像即可;
(3)a.根据第(2)问y坐标表达式可得H与c关系式,进一步求解c的表达式,再根据图b求解半个周期内电压与时间的关系式,联立即可得到c与1t的关系式,根据关系式即可证明c与1t的图像在0
本题考查带电粒子在电场中的运动,要求学生能正确分析带电粒子的运动过程和运动性质,熟练应用对应的规律解题。
19.【答案】解:(1)不计轮轴间的摩擦力和空气阻力,不计滑轮质量,两物体组成系统机械能守恒,则有:
3mgh=12×3mv2+12mv2+mgh
解得两物体的速度大小为:v= gh
(2)a.线速度与角速度的关系为:v=ωr,可得:ω=vr
类比此关系,可得角加速度α与半径为r的圆盘边缘的线加速度a的关系为:
α=ar
质点的牛顿第二定律表达式为:F=ma
刚体转动过程中:合力矩M类比于合力F、转动惯量I类比于质量m、角加速度α类比于加速度a。
可得合力矩、转动惯量和角加速度的关系为:
M=Iα
b.质点的平动动能为:Ek=12mv2,通过类比可得刚体转动角速度为ω时刚体的转动动能为:
Ek转=12Iω2
c.滑轮的转动惯量的表达式为:I=12mR2
规定使物体逆时针旋转的力矩方向为正方向,则有:
拉力T1的力矩为M1=T1R
拉力T1的力矩为M2=−T2R
设物体A、B的加速度大小为a,可得滑轮的角加速度为:α=aR
根据:M=Iα,可得:
M1+M2=Iα
代入整理得:T1−T2=12ma
再由牛顿第二定律得:
对A有:3mg−T1=3ma
对B有:T2−mg=ma
联立解得:T1=53mg,T2=139mg
设物体A下落高度h后的速度大小为v1,此时滑轮的转动动能为:
Ek转=12Iω2=12⋅12mR2⋅(v1R)2=14mv12
两物体和滑轮组成系统机械能守恒,则有:
3mgh=12×3mv12+12mv12+mgh+14mv12
解得:v1=23 2gh
答:(1)物体A下落高度h后,两物体的速度大小为 gh。
(2)a.角加速度与半径为r的圆盘边缘的线加速度a的关系为α=ar,刚体转动过程中合力矩、转动惯量和角加速度的关系为M=Iα;
b.刚体转动角速度为ω时刚体的转动动能Ek转为12Iω2;
c.与物体A相连的轻绳拉力大小T1为53mg,与物体B相连的轻绳拉力大小T2为139mg,物体A下落高度h后的速度大小为23 2gh。
【解析】(1)两物体组成系统机械能守恒,根据机械能守恒定律求解;
(2)a.根据线速度与角速度的关系,类比求解角加速度α与线加速度a的关系;
刚体转动过程中合力矩M类比于合力F、转动惯量I类比于质量m、角加速度α类比于加速度a。类比质点的牛顿第二定律表达式求解可得合力矩、转动惯量和角加速度的关系;
b.类比质点的平动动能可得刚体转动角速度为ω时刚体的转动动能;
c.确定两个拉力对滑轮的力矩,根据前述得到的关系式,结合质点的牛顿第二定律求解;根据转动动能的表达式得到滑轮的转动动能,根据两物体和滑轮组成系统机械能守恒求解。
本题通过类比的方法展示了刚体转动过程中,刚体的合力矩M与角加速度的关系,以及转动动能的概念和表达式。重在理解,物理量一一对应即可解题。
20.【答案】解:(1)cd边刚进入磁场时产生的感应电动势为:E=NBLv0…①
根据闭合电路的欧姆定律可得,此时线框内感应电流的大小为:I=ER…②
由①②可解得:I=NBLv0R…③
由右手定则可判断出线框内感应电流的方向为顺时针;
(2)cd边刚进入磁场时,有:F合=F安=NBIL=ma…④
由③④可解得:a=N2B2L2v0mR
(3)由法拉第电磁感应定律可知此过程中产生的平均感应电动势为:E−=NBL2△t…⑤
平均感应电流为:I−=E−R…⑥
此过程中通过线圈的电荷量为:q=I−△t…⑦
由⑤⑥⑦可解得:q=NBL2R
由能量守恒定律可得:Q=12mv02−12m(v2)2…⑧
由⑧可解得:Q=38mv02
答:(1)cd边刚进入磁场时线框内感应电流的大小I=NBLv0R,方向为顺时针方向;
(2)cd边刚进入磁场时,小车的加速度大小得a=N2B2L2v0mR;
(3)若小车完全进入磁场时速度为v02,在此过程中通过线圈的电荷量为q=NBL2R;线圈产生的焦耳热为Q=38mv02。
【解析】(1)要计算感应电流的大小,可根据闭合电路欧姆定律先求解出感应电动势大小再进行计算,求解感应电动势可根据电磁感应定律进行求解,方向可根据右手定则进行判断;
(2)要计算加速度,要先进行受力分析,分析出合外力根据牛顿第二定律进行求解;
(3)要计算电荷量,需根据q=I−△t进行计算,就必须先根据电磁感应定律表示出平均感应电动势,再表示出平均感应电流即可代入求解;要计算焦耳热,可根据能量守恒定律直接列式求解。
本题是对电磁感应定律、牛顿第二定律、能量守恒定律、闭合电路欧姆定律等知识的综合考查,但比较容易分析,过程比较简单。几种金属逸出功和极限频率
金属
W0/eV
ν/1014Hz
钠
2.29
5.33
钾
2.25
5.44
铷
2.13
5.15
2024年山东省实验中学高考物理一模试卷(含详细答案解析): 这是一份2024年山东省实验中学高考物理一模试卷(含详细答案解析),共27页。试卷主要包含了单选题,多选题,实验题,简答题等内容,欢迎下载使用。
2024年北京师大附属实验学校高考物理模拟试卷(含详细答案解析): 这是一份2024年北京师大附属实验学校高考物理模拟试卷(含详细答案解析),共26页。试卷主要包含了单选题,多选题,实验题,简答题等内容,欢迎下载使用。
2024年北京八十中高考物理零模试卷(含详细答案解析): 这是一份2024年北京八十中高考物理零模试卷(含详细答案解析),共21页。试卷主要包含了单选题,实验题,计算题等内容,欢迎下载使用。












