

2024年江苏省决胜新高考联盟高考物理联考试卷(2月份)(含详细答案解析)
展开1.随着航天技术的不断发展,太空中的航天器数量越来越多。假设太空中的航天器围绕地球做匀速圆周运动,下列说法正确的是( )
A. 航天器的转速一定大于地球的转速
B. 离地面越高的航天器向心加速度越小
C. 同一轨道上的航天器受到的地球引力相等
D. 同一轨道上的航天器一定不会发生碰撞现象
2.某型号酒精测试仪的工作原理图如图所示,传感器R的阻值随气体中酒精浓度的增大而减小。当一位酒驾驾驶员对着测试仪吹气时( )
A. 传感器的电阻增大
B. 电流表的示数变小
C. 电压表的示数变大
D. 电源的总功率增大
3.在恒星内部发生的核反应 11H+X→Y和 11H+Y→815O中,X、Y代表两种不同的原子核,则( )
A. X、Y是同位素B. X的结合能比Y的大
C. Y的核子数与 815O相等D. X的中子数为7
4.如图所示,在足够大的、磁感应强度为B的匀强磁场中,一匝数为N、面积为S的矩形金属线框绕与磁感线垂直的转轴匀速转动,则当线框平面与中性面( )
A. 垂直时,线框的四条边受到安培力
B. 垂直时,线框的磁通量变化率最大
C. 重合时,线框产生的感应电动势最大
D. 重合时,穿过线框的磁通量为NBS
5.在光学元件的表面镀一层特定厚度的薄膜,可增加光的透射。某薄膜能增加一单色光的透射,该薄膜的最小厚度( )
A. 小于单色光波长的四分之一B. 等于单色光波长的四分之一
C. 等于单色光波长的二分之一D. 大于单色光波长的二分之一
6.功率为P的白炽灯消耗的电功率有k%产生红光。已知红光的波长为λ,红光在真空中的光速为c,则该白炽灯1s内发出的红光光子数为( )
A. Pλhc⋅k%B. hcPλ⋅k%C. Pλhc⋅k%D. hcPλ⋅k%
7.一列简谐横波在t=0时的波形图如图所示。介质中x=2m处的质点P沿y轴方向做简谐运动的表达式为y=10sin(5πt)cm,则( )
A. 这列波的波长为6m
B. 这列波的传播速度为1m/s
C. t=0.1s时,P处于平衡位置处
D. x=3m处质点的振动方程为y=10sin(5πt−π2)cm
8.用插针法测量矩形玻璃砖折射率的实验中,入射光线和出射光线上大头针的位置均正确,则逆着出射光线观察到的4个大头钉的位置可能是( )
A. B.
C. D.
9.如图所示,外力使条形磁铁甲、乙静止于水平桌面上,已知甲的质量小于乙的质量,两者与桌面间的动摩擦因数相等。现同时释放甲、乙,两者均相对于桌面运动,在它们接近过程中的任一时刻( )
A. 甲的加速度比乙的小B. 甲的动能比乙的大
C. 甲的动量比乙的小D. 磁场力对甲、乙的功率相等
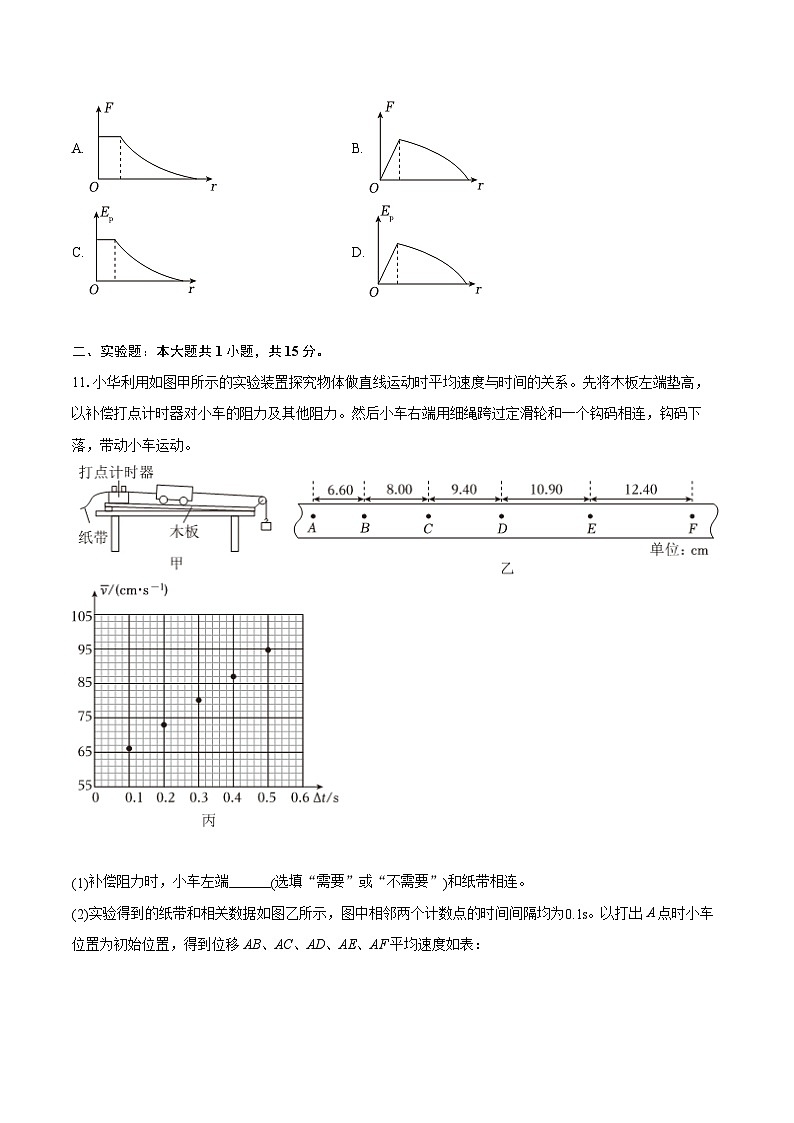
10.如图所示,均匀带正电的薄球壳上有一小孔A,带正电的试探电荷(不计重力)从球心O以足够大的初速度沿OA方向射出。取无穷远处的电势为0,则关于试探电荷受到的电场力大小F、电势能Ep与离开球心的距离r的关系图像可能正确的是( )
A. B.
C. D.
二、实验题:本大题共1小题,共15分。
11.小华利用如图甲所示的实验装置探究物体做直线运动时平均速度与时间的关系。先将木板左端垫高,以补偿打点计时器对小车的阻力及其他阻力。然后小车右端用细绳跨过定滑轮和一个钩码相连,钩码下落,带动小车运动。
(1)补偿阻力时,小车左端______(选填“需要”或“不需要”)和纸带相连。
(2)实验得到的纸带和相关数据如图乙所示,图中相邻两个计数点的时间间隔均为0.1s。以打出A点时小车位置为初始位置,得到位移AB、AC、AD、AE、AF平均速度如表:
请根据表中数据,在方格纸上补全实验点,(如图丙)作出v−−Δt图线。
(3)从实验结果可知,小车运动的v−−Δt图线可视为一条直线,从图线可得到打出A点时小车速度大小vA=______cm/s。
(4)设v−−Δt图线的斜率为k,可得到小车的加速度大小a=______。
(5)小明认为若再增加一个钩码,不改变其他条件,重新实验作出的v−−Δt图线的斜率为2k。请判断该观点是否正确,并简要说明理由。______。
三、简答题:本大题共4小题,共45分。
12.一瓶内装有氧气。已知氧气的分子数为N,密度为ρ,摩尔质量为M,温度为T。阿伏伽德罗常数为NA。
(1)求瓶内氧气的体积V;
(2)升高氧气温度并释放出瓶内部分氧气以保持瓶内压强不变,求氧气温度升至T′时瓶内氧气的密度ρ′。
13.如图所示,两条相距为d的平行金属导轨位于竖直面内,其上端接一阻值为R1的电阻,匀强磁场区域的磁感应强度大小为B、方向与导轨平面垂直。质量为m、电阻为R2的金属杆在外力作用下静止在导轨上,当磁场区域(虚线以下足够大的空间)以速度v0竖直向下匀速运动后,释放金属杆。导轨的电阻不计,导轨光滑且足够长,杆在运动过程中始终在磁场中,并与导轨垂直且两端与导轨保持良好接触,重力加速度为g。求:
(1)释放金属杆瞬间,杆中感应电流的大小I;
(2)经过足够长的时间后,金属杆的速度大小v。
14.如图所示,轻杆的一端固定在轻质竖直转轴上的O点,杆与轴的夹角a=60∘,杆上套有一劲度系数k=100N/m的轻质弹簧,弹簧一端固定于O点,另一端与套在杆上的质量m=1kg的圆环相连,杆和圆环均处于静止状态。已知弹簧原长L0=0.15m,弹簧始终在弹性限度内,取重力加速度g=10m/s2,不计一切摩擦。
(1)求圆环静止时弹簧的长度L;
(2)在外力作用下,杆随转轴缓慢加速转动,圆环始终未离开杆。
①当弹簧处于原长时,求杆转动的角速度大小ω0;
②求杆的角速度从0到ω0的过程中,外力做的功W。
15.如图所示,磁感应强度为B的匀强磁场垂直于xOy平面向外。质量为m、电荷量为+q的粒子从坐标原点O垂直磁感线入射到磁场中,初速度大小为v0,方向与x轴正方向成30∘角,粒子能经过x轴上的P点。不计粒子重力。
(1)求点P的坐标;
(2)若仅将磁场替换为在坐标平面内且沿y轴负方向的匀强电场,粒子仍能经过P点,题干中的B为已知量,其他条件不变。求电场强度的大小E;
(3)若仅在坐标平面内增加沿y轴正方向的匀强电场,电场强度E′=( 3−1)v0B2,求粒子离x轴的最远距离ym。
答案和解析
1.【答案】B
【解析】解:A、根据万有引力提供向心力有GMmr2=m⋅4π2n2⋅r,解得n= GM4π2r3,可知如果航天器的轨道半径大于或等于地球同步卫星轨道半径,则航天器的转速小于或等于地球同步卫星的转速,而地球同步卫星的转速与地球转速相等,所以航天器的转速小于或等于地球的转速,故A错误;
B、根据万有引力提供向心力,有GMmr2=ma,得向心加速度a=GMr2,故离地面越高的航天器向心加速度越小,故B正确;
C、根据万有引力公式F=GMmr2,又航天器的质量未知,所以同一轨道上的航天器受到的地球引力不一定相等,故C错误;
D、由GMmr2=mv2r,v= GMr,可知同一轨道上的航天器的线速度的大小相等,如果它们绕地球飞行的运转方向相反,它们会碰撞,故D错误。
故选:B。
根据万有引力提供向心力列出相对应的方程即可求解判断。
本题主要考查万有引力定律的应用,解题关键是根据万有引力提供向心力求出转速,向心加速度和线速度的表达式进行判断。
2.【答案】D
【解析】解:ABC、依题意,传感器电阻R的阻值随酒精气体浓度的增大而减小,则酒驾驾驶员对着测试仪吹气时,传感器R的阻值减小,则电路的总电阻减小,电路中的电流增大,根据U=E−I(R0+r),可知电压表示数变小,故ABC错误;
D、电路中的电流增大,根据电源总功率的公式P=EI可知电源的总功率增大,故D正确;
故选:D。
传感器电阻R的阻值随酒精气体浓度的增大而减小,据此分析传感器的电阻变化,从而判断电路的总电阻的变化以及总电流的变化,再根据闭合电路的欧姆定律分析电压表示数的变化。根据P=EI分析电源总功率的变化。
本题主要考查酒精传感器的运用,掌握闭合电路的欧姆定律、功率公式是解题的关键。
3.【答案】D
【解析】解:AB.由 11H+X→Y可知,Y的电荷数比X的电荷数多1,所以X、Y不是同位素;Y的质量数比X的质量数大,所以Y的结合能比X的大,故AB错误;
C.由 11H+Y→815O可知,Y的核子数比 815O少1,故C错误;
D.由 11H+Y→815O, 11H+X→Y,结合反应过程质量数和电荷数守恒,可知Y的质量数
15−1=14,电荷数8−1=7;则X的质量数14−1=13,电荷数7−1=6,则X的中子数为
13−6=7
故D正确。
故选:D。
根据质量数守恒以及质子数守恒分析Y粒子和X粒子。
本题考查了核反应中核子的质量数和电荷数守恒,进而用来判断参与反应的物质的电荷数和质量数。
4.【答案】B
【解析】解:A.当线框平面与中性面垂直时,上下两边的电流方向与磁感线平行,所以上下两边不受安培力,故A错误;
B.当线框平面与中性面垂直时,磁通量为零,此时线框的磁通量变化率最大,感应电动势最大,B正确;
CD.当线框平面与中性面重合时,磁通量最大,线框产生的感应电动势最小为0,磁通量为
Φ=BS
故CD错误;
故选:B。
当线圈平面与磁感线平行时,感应电动势最大,磁通量为零,磁通量的变化率最大,当线圈平面与磁感线垂直时,感应电动势最小,磁通量最大,磁通量的变化率为零。
本题关键明确中性面是磁通量最大、感应电动势为零的位置,每次经过中性面,而垂直中性面位置是感应电动势最大的位置。
5.【答案】A
【解析】解:增透膜的原理是让薄膜的前后表面的反射光在前表面相遇时能实现干涉相消,则需要两列光相遇时是波峰与波谷相叠加,即反射光的总强度接近于零,因而大大减少了光的反射损失,从而增加了透视光的强度,所以薄膜的最小厚度对应两束反射光的光程差恰好是光在这种介质中的波长的12,所以薄膜的最小厚度等于该单色光在这种介质中的波长的14;由于光进入介质后频率不变,波速减小,则波长减小,所以该薄膜的最小厚度小于单色光波长的四分之一,故A正确,BCD错误。
故选:A。
根据路程差至少等于半个波长求解薄膜的最小厚度。
本题考查了光的干涉原理,要知道波程差为半波长的奇数倍时为减弱点,从而来理解增透膜的原理。
6.【答案】A
【解析】解:一个红光光子的能量为:
E=hν
根据波速与波长关系得:
ν=cλ
白炽灯在时间1s内辐射的红光的能量为Pk%,辐射的光子数为:
n=Pk%E
联立解得:n=λPk%hc,故A正确,BCD错误
故选:A。
根据波速与波长关系和E=hν公式计算一个红光光子的能量,根据功率为P的白炽灯消耗的电功率有k%产生红光,求出每秒发出的可见光的光子数。
该题考查光子的能量的公式结合电功率再应用E=hν是求光子数的关键。
7.【答案】D
【解析】解:A.根据波形图可知该波的波长为4m,故A错误;
B.根据y=10sin(5πt)cm可得该波的周期为:T=2πω=2π5πs=0.4s,则波速为:v=λT=40.4m/s=10m/s,故B错误;
C.由于t=0.1s=14T,根据波形图可知,t=0.1s时,P处于波峰或波谷处,故C错误;
D.t=0时,x=3m处质点处于波谷,即初相为−π2,故x=3m处质点的振动方程为y=10sin(5πt−π2)cm,故D正确。
故选:D。
根据波形图直接得到该波的波长;根据T=2πω求解周期;根据振动情况分析t=0.1s时P的位置;t=0时,x=3m处质点处于波谷,即初相为−π2,由此得到振动方程。
本题主要是考查了波的图像;解答本题关键是要掌握振动的一般方程y=Asinωt,知道方程中各字母表示的物理意义,能够根据图像直接读出振幅、波长和各个位置处的质点振动方向,知道波速、波长和频率之间的关系v=fλ。
8.【答案】C
【解析】解:设入射光线和出射光线上大头针分别为P1、P2和P3、P4,用插针法测量矩形玻璃砖折射率的实验中,在直线AO(入射光线)上竖直插上两枚大头针P1、P2,透过玻璃砖观察大头针P1、P2的像,调整视线方向,直到P2挡住P1的像;在玻璃砖的另一侧插上大头针P3,调整P3位置,透过玻璃砖使P3挡住P1、P2的像;在P3同侧插上P4,调整P4位置,使P4挡住P3以及P1、P2的像;
根据上述分析,玻璃砖中只能看到一颗大头针,玻璃砖外还会出现大头针P1、P2的上部分,故ABD错误,C正确。
故选:C。
根据实验的正确操作步骤分析作答。
本题主要考查了“插针法”测定玻璃的折射率,关键是要掌握正确的实验操作步骤。
9.【答案】B
【解析】解:A.对甲、乙两条形磁铁水平方向分别做受力分析,如图所示
根据牛顿第二定律有
a甲=F−μm甲gm甲、a乙=F−μm乙gm乙
可得甲的加速度比乙的大,故A错误;
B.由于两物体运动时间相同,且同时由静止释放,甲的加速度较大,则甲的位移较大,根据动能定理有
(F−μm甲g)x=Ek
可知甲的动能比乙的大,故B正确;
C.对于整个系统而言,由于合力方向向右,合冲量方向向右,所以合动量方向向右,故甲的动量大小比乙的大,故C错误;
D.根据功率公式
P=Fv
由于甲、乙的速度不同,可知磁场力对甲、乙的功率不相等,故D错误。
故选:B。
根据牛顿第二定律推导加速度分析判断;根据位移和合力大小的分析,依据动能定理判断动能的大小;根据合动量方向分析判断甲、乙动量大小;根据功率公式判断甲、乙的功率大小。
本题关键是掌握两磁铁运动过程的位移和受力情况的分析。
10.【答案】C
【解析】解:由于球壳内的场强处处为零,试探电荷在球壳内不受电场力,电场力不做功,试探电荷的电势能保持不变。球壳内的场强随着离圆心的距离r的增加而减小,带正电的试探电荷受到的电场力方向与速度方向相同,电场力做正功,试探电荷的电势能随着r的增加而增加,但增加得越来越慢,故C正确,ABD错误;
故选:C。
理解球壳内外的场强变化趋势,结合图像的物理意义完成分析。
本题主要考查了电势能与电场力做功的关系,熟悉球壳内外的场强分布特点即可完成分析,难度不大。
11.【答案】需要 59 2 k 不正确,因为再增加一个钩码后,小车的加速度小于原来的2倍,即斜率小于2k
【解析】解:(1)补偿阻力时,不仅补偿木板和小车之间的阻力,还需补偿纸带与打点计时器之间阻力,小车左端需要和纸带相连,故填“需要”。
(2)利用表格中的数据作出v−−Δt图线,如图所示。
(3)由v−−Δt图线知,纵轴的截距为A点的速度,vA=59cm/s。
(4)小车做匀变速直线运动,有
x=v0t+12at2
整理变形可得
xt=v0+12at
故小车在t=0时,即打出A点时小车的速度大小
vA=b
小车的加速度大小a满足
12a=k
即
a=2k
(5)如果不满足钩码质量m′远小于小车质量M,则钩码质量不能忽略,则有
m′g=(m′+M)a′
整理变形得
a′=m′gm′+M
所以当不满足钩码质量远小于小车质量时,加速度变小,因为再增加一个钩码后,小车的加速度小于原来的2倍,即斜率小于2k,故不正确。
故答案为:(1)需要
(2)
(3)59cm/s
(4)2k
(5)不正确,因为再增加一个钩码后,小车的加速度小于原来的2倍,即斜率小于2k。
(1)纸带与打点计时器之间也有阻力,不可省略,应前后一致;
(2)利用表格所给数据描点;
(3)由(2)图像找到A点时速度大小;
(4)利用运动学公式计算加速度;
(5)可利用牛顿第二定律判断是否需要增加钩码。
本题结合直线运动规律问题考查学生实验探究的能力,其中重点考查处理数据的能力,灵活应用牛顿第二定律为解决本题第5问的关键。
12.【答案】解:(1)氧气的质量
m=NNAM
瓶内氧气的体积V=mρ,解得
V=NMNAρ
(2)升高氧气温度并释放出瓶内部分氧气以保持瓶内压强不变,则
VT=V′T′
质量相等,则
ρV=ρ′V′
解得
ρ′=ρTT′
答:(1)瓶内氧气的体积为NMNAρ;
(2)氧气温度升至T′时瓶内氧气的密度为ρTT′。
【解析】(1)根据摩尔质量的计算公式结合密度的计算公式解答;
(2)根据盖-吕萨克定律结合质量相等解答。
本题考查其他的等压变化,解题关键掌握气体质量不变及密度的计算公式。
13.【答案】解:(1)释放金属杆瞬间,金属杆相对于磁场运动的速度大小为v0,产生的感应电动势大小为
E=Bdv0
由闭合电路的欧姆定律得
I=ER1+R2
解得:I=Bdv0R1+R2
(2)经过足够长的时间后,金属杆做匀速直线运动,则有
mg=BI′d
感应电动势为
E′=Bd(v−v0)
感应电流为
I′=E′R1+R2
联立解得:v=mg(R1+R2)B2d2+v0
答:(1)释放金属杆瞬间,杆中感应电流的大小I为Bdv0R1+R2;
(2)经过足够长的时间后,金属杆的速度大小v为mg(R1+R2)B2d2+v0。
【解析】(1)释放金属杆瞬间,根据感应电动势公式E=Bdv0可求出金属杆产生的感应电动势,结合闭合电路的欧姆定律求解杆中感应电流的大小。
(2)经过足够长的时间后,金属杆做匀速直线运动,根据感应电动势公式、闭合电路的欧姆定律、安培力公式和平衡条件相结合求解金属杆的速度大小v。
解答本题时,要根据金属杆相对于磁场的速度来求感应电动势,结合闭合电路的欧姆定律、安培力公式和平衡条件进行解答。
14.【答案】解:(1)对圆环受力分析,平行于杆方向根据平衡条件有
mgcsα=kΔx
弹簧的长度为
L=L0−Δx
代入数据联立解得
L=0.10m;
(2)当弹簧处于原长时,对圆环受力分析如图所示
对圆环根据牛顿第二定律有
mgtanα=mω02r
根据几何关系有
r=L0sinα
代入数据联立解得
ω0=203rad/s;
(3)杆的角速度从0到ω0的过程中,根据动能定理得
W+W弹+G=12mv2−0
弹簧弹力做的功为
W弹=kΔx+02Δx=12k(Δx)2
重力做的功为
G=−mgΔxcsα
圆环的线速度为
v=ω0r
代入数据联立解得
W=0.50J。
答:(1)圆环静止时弹簧的长度L为0.10m;
(2)在外力作用下,杆随转轴缓慢加速转动,圆环始终未离开杆。
①当弹簧处于原长时,杆转动的角速度大小ω0为203rad/s;
②杆的角速度从0到ω0的过程中,外力做的功W为0.50J。
【解析】(1)根据平衡条件和弹簧的长度关系列式,联立求解圆环静止时弹簧的长度;
(2)①根据几何知识求解圆环做圆周运动的半径,根据牛顿第二定律求解杆转动的角速度大小;
②根据动能定理求解外力做的功。
本题考查功能关系,要求学生能正确分析物体的运动过程和运动性质,熟练应用对应的规律解题。
15.【答案】解:(1)洛伦兹力提供向心力:qv0B=mv02R
由几何关系有:xp=OP−=2Rsin30∘
代入解得点P的坐标为(mv0qB,0)。
(2)带电粒子在x轴方向做匀速直线运动:OP−=v0cs30∘⋅t
y轴方向做竖直上抛运动:2v0sin30∘=at
而加速度:a=qEm
解得:E= 3v0B2
(3)将粒子水平方向的初速度分解为两个速度:v0cs30∘=v1+v2
其中:qE′=qv1B
代入E′值的大小解得:v2=v02
所以带电粒子的运动为速率为v1、向右的匀速直线运动和速率为v= 2v02的匀速圆周运动的合运动,
洛伦兹力提供向心力:qvB=mv2R′,圆周分运动轨迹如图所示,
几何关系:ym=R′(1+sin45∘)
联立解得:ym=( 2+1)mv02qB
答:(1)点P的坐标为(mv0qB,0);
(2)电场强度的大小E为 3v0B2;
(3)粒子离x轴的最远距离ym为( 2+1)mv02qB。
【解析】(1)带电粒子在匀强磁场中做匀速圆周运动,根据洛伦兹力等于向心力结合几何关系求交点坐标;
(2)换为电场后,粒子做类斜抛运动,在平行电场方向列出时间表达式,在垂直于电场方向列出位移表达式,结合牛顿第二定律求电场强度的大小;
(3)用配速法确定做匀速圆周运动的速度大小,根据洛伦兹力提供向心力求轨道半径,再由几何关系求最远距离。
本题考查了带电粒子在磁场、电场及叠加场中运动的综合,难点是在叠加中的运动性质的确定,用配速法,结合半径公式、几何关系进行求解。位移区间
AB
AC
AD
AE
AF
Δt/s
0.1
0.2
0.3
0.4
0.5
v−(cm/s)
66.0
73.0
80.0
87.3
94.6
2024年江苏省苏州市高考物理模拟试卷(含详细答案解析): 这是一份2024年江苏省苏州市高考物理模拟试卷(含详细答案解析),共19页。试卷主要包含了单选题,实验题,简答题等内容,欢迎下载使用。
2024年江苏省无锡市等4地高考物理一模试卷(含详细答案解析): 这是一份2024年江苏省无锡市等4地高考物理一模试卷(含详细答案解析),共18页。试卷主要包含了单选题,实验题,简答题等内容,欢迎下载使用。
2024年江苏省常州市前黄高级中学高考物理模拟试卷(含详细答案解析): 这是一份2024年江苏省常州市前黄高级中学高考物理模拟试卷(含详细答案解析),共20页。试卷主要包含了单选题,实验题,简答题,计算题等内容,欢迎下载使用。












