初中数学苏科版八年级下册9.3 平行四边形复习练习题

这是一份初中数学苏科版八年级下册9.3 平行四边形复习练习题，文件包含专题05几何思想之特殊平行四边形难点综合专练原卷版-考点培优尖子生专用2021-2022学年八年级数学下册专题训练苏科版docx、专题05几何思想之特殊平行四边形难点综合专练解析版-考点培优尖子生专用2021-2022学年八年级数学下册专题训练苏科版docx等2份试卷配套教学资源，其中试卷共58页， 欢迎下载使用。
一、单选题
1．（2021·江苏宜兴·八年级期中）如图，在△ABC中，AB＝4，∠ABC＝60°，∠ACB＝45°，D是BC的中点，直线l经过点D，AE⊥l，BF⊥l，垂足分别为E，F，则AE+BF的最大值为（ ）
A．B．C．D．
【标准答案】B
【思路指引】
把要求的最大值的两条线段经过平移后形成一条线段，然后再根据垂线段最短来进行计算即可．
【详解详析】
解：如图，过点作于点，过点作于点，
在Rt△AHB中，
，，
，，
在中，，
，
，
点为中点，
，
在与中，
，
，
，
延长，过点作于点，得矩形，
，
，
在中，，
当直线时，最大值为，
综上所述，的最大值为．
故选：．
【名师指路】
本题主要考查了全等三角形的判定定理和性质定理及矩形的性质，构建全等三角形是解答此题的关键．
2．（2021·江苏工业园区·八年级月考）已知菱形的两条对角线分别为12和16，M、N分别是边、的中点，P是对角线上一点，则的最小值为（ ）

A．6B．8C．10D．12
【标准答案】C
【思路指引】
作M关于BD的对称点Q，连接NQ，交BD于P，连接MP，此时MP+NP的值最小，连接AC，求出CP、BP，根据勾股定理求出BC长，证出MP+NP＝QN＝BC，即可得出答案．
【详解详析】
解：作M关于BD的对称点Q，连接NQ，交BD于P，此时最小，最小值为QN长，连接MP、AC．

∵四边形ABCD是菱形，
∴AB=BC＝CD，∠ABP＝∠MBP，
∴点Q在AB上．
∵M为BC中点，BQ＝BM．
∴Q为AB中点．
∵N为CD中点，
∴BQ∥CD，BQ＝CN．
∴四边形BQNC是平行四边形．
∴NQ＝BC，P是AC、BD中点．
∴CP＝AC＝6，BP＝BD＝8．
在Rt△BPC中，由勾股定理得：BC＝＝10，即NQ＝10，
∴MP+NP＝QP+NP＝QN＝10．
故选：C．
【名师指路】
本题考查了轴对称﹣最短路线问题，平行四边形的性质和判定，菱形的性质，勾股定理的应用，解此题的关键是能利用轴对称找出P的位置．
3．（2021·江苏·张家港市梁丰初级中学八年级月考）如图，在矩形中，，，P是边上任意一点，，，垂足分别是E，F，那么（ ）
A．B．C．D．无法确定
【标准答案】A
【思路指引】
结合矩形的特点利用勾股定理求出对角线的长，再三角形不同的面积表示方法求出并求出AG的长，即求出．
【详解详析】
解：如图：过点A作AG⊥BD于点G，连接PO
∵在矩形中，，OA=OD，
∴ ，
∵，
∴，
∵，，
∴ ，
∵，
∴ ，
∴．
故选：A．
【名师指路】
此题利用矩形考查三角形面积表示方法，涉及到勾股定理，利用面积相等用不同的面积公式求解线段长度．
4．（2021·江苏·苏州市景范中学校八年级月考）如图，在中，为斜边的中线，过点D作于点E，延长至点F，使，连接，点G在线段上，连接，FG=2,GC=3且，下列结论：①；②四边形是平行四边形；③．其中正确结论的个数是（ ）
A．0个B．1个C．2个D．3个
【标准答案】D
【思路指引】
根据直角三角形的性质知DA=DB=DC，根据等腰三角形的性质结合菱形的判定定理可证得四边形ADCF为菱形，继而推出四边形DBCF为平行四边形，可判断①②；利用邻补角的性质结合已知可证得∠CFE =∠FGE，即可判断③．
【详解详析】
解：∵在中，为斜边的中线，
∴DA=DB=DC，
∵于点E，且，
∴AE=EC，
∴四边形ADCF为菱形，
∴FC∥BD，FC=AD=BD，FE=DE=DF
∴四边形DBCF为平行四边形，故②正确；
∴DF=BC，
∴DE=BC，故①正确；
∵四边形ADCE为菱形，
∴CF=CD，
∴∠CFE=∠CDE，
∵∠CDE+∠EGC=180，而∠FGE+∠EGC=180，
∴∠CDE=∠FGE，∠CFE =∠FGE，
∴EF=EG，故③正确；
综上，①②③都正确，
故选D．
【名师指路】
本题考查了菱形的判定和性质、直角三角形的性质、等腰三角形的性等知识，解题的关键在于能够熟练掌握相关知识进行求解．
5．（2021·江苏·苏州湾实验初级中学八年级月考）如图，在中，，，，P为边上一动点，于E，于F，M为的中点，则的最小值为（ ）
A．B．C．D．
【标准答案】A
【思路指引】
先求证四边形AFPE是矩形，再根据直线外一点到直线上任一点的距离，垂线段最短，利用面积法可求得AP最短时的长，然后即可求出AM最短时的长．
【详解详析】
解：连接AP，在△ABC中，AB=3，AC=4，∠BAC=90°，
∴
∵PE⊥AB，PF⊥AC，
∴四边形AFPE是矩形，
∴EF=AP．EF与AP互相平分，
∵M是EF的中点，
∴AP过点M，M为AP中点，
∴AM=AP，
根据直线外一点到直线上任一点的距离，垂线段最短，
即AP⊥BC时，AP最短，同样AM也最短，
∴S△ABC=BC•AP＝AB•AC，
∴×5AP＝×3×4，
∴AP最短时，AP=，
∴当AM最短时，AM=AP=．
故选A．
【名师指路】
此题主要考查学生对勾股定理的应用、矩形的判定和性质、垂线段最短和直角三角形斜边上的中线的理解和掌握，此题涉及到动点问题，有一定难度．
6．（2021·江苏工业园区·八年级月考）如图，以正方形的一边向形外作等边，与交于点，且DF=EF，则等于（ ）
A．B．C．D．
【标准答案】A
【思路指引】
分别求证△DCF≌△DAF≌△EAF可得∠DFC=∠AFD=∠AFE，根据∠DFC+∠AFD+∠AFE=180°，可得∠DFC=∠AFD=∠AFE=60°．
【详解详析】
解：连接AC，
∵BD为AC的垂直平分线，
∴FA=FC，
∵四边形ABCD是正方形，
∴AD=DC=AB，
在△DCF和△DAF中，
，
∴△DCF≌△DAF，
∵三角形ABE是等边三角形，
∴AE=AB=AD，
在△DAF和△EAF中，
，
∴△DAF≌△EAF，
∴△DCF≌△DAF≌△EAF，
得：∠DFC=∠AFD=∠AFE，
又∵∠DFC+∠AFD+∠AFE=180°，
∴∠DFC=∠AFD=∠AFE=60°，
故选：A．
【名师指路】
本题考查了正方形各边长相等的性质，考查了正三角形各边长相等的性质，本题中求证△DCF≌△DAF≌△EAF是解题的关键．
（2021·江苏崇川·八年级期末）顺次连接矩形各边中点所得四边形必定是（ ）．
A．平行四边形B．矩形C．正方形D．菱形
【标准答案】D
【思路指引】
作出图形，根据三角形的中位线定理可得，，再根据矩形的对角线相等可得，从而得到四边形的四条边都相等，然后根据四条边都相等的四边形是菱形解答．
【详解详析】
解：如图，连接、，
、、、分别是矩形的、、、边上的中点，
，（三角形的中位线等于第三边的一半），
矩形的对角线，
，
四边形是菱形．
故选：D．
【名师指路】
本题考查了中点四边形，三角形的中位线定理，菱形的判定，矩形的性质，作辅助线构造出三角形，然后利用三角形的中位线定理是解题的关键．
8．（2021·江苏海州·八年级期中）将矩形纸片 ABCD按如图所示的方式折叠，恰好得到菱形 AECF．若AB=4，则菱形AECF边长为（ ）
A．2.6B．3C．D．
【标准答案】D
【思路指引】
根据菱形AECF，设BE为x，则AE为4-x，CE为4-x，得∠FCO=∠ECO，可通过折叠的性质得到ECO=∠ECB，可知，结合直角三角形勾股定理求得BE的长．
【详解详析】
四边形AECF是菱形，AB=4，
设BE为x，则AE为4-x，CE为4-x，

，即为菱形的边长．
故选:D．
【名师指路】
此题主要考查了矩形的折叠问题等知识，涉及菱形的性质和直角三角形，解题过程中应注意折叠是一种对称变换，折叠前后图形的形状和大小不变，如本题中折叠前后角相等．
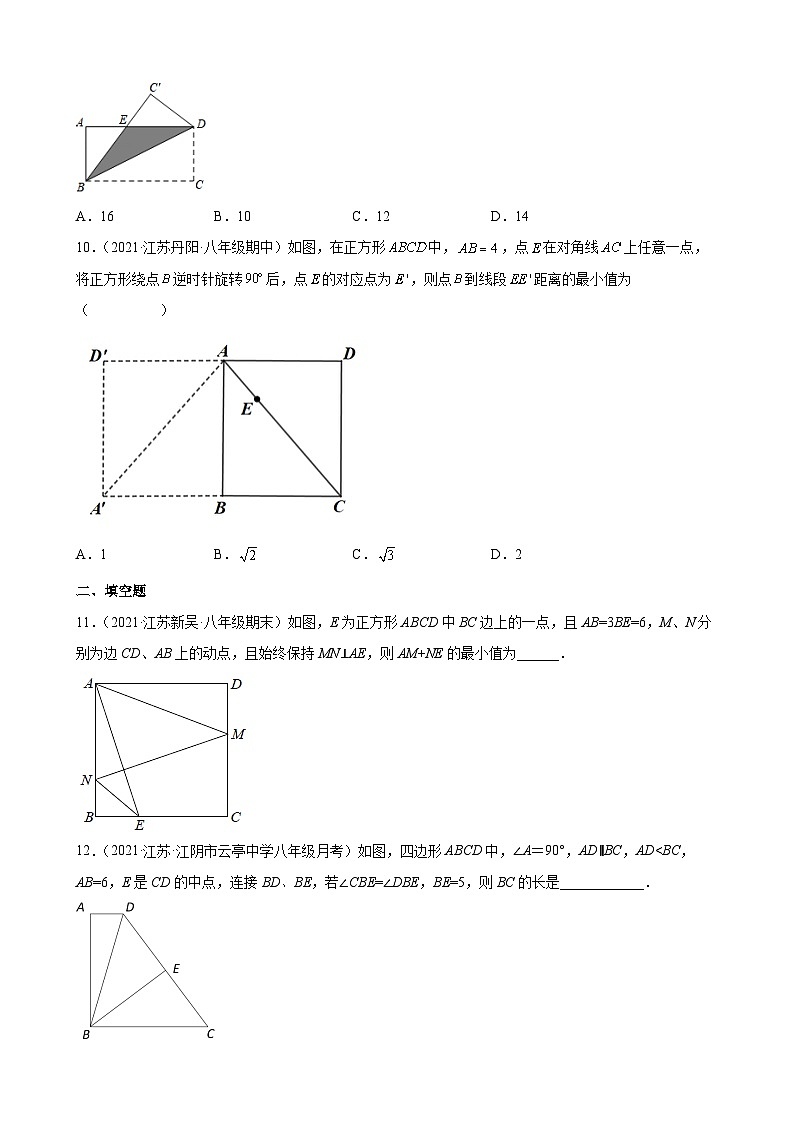
9．（2021·江苏·星海实验中学八年级期中）如图，矩形ABCD中，AB＝6，如果将该矩形沿对角线BD折叠，那么图中阴影部分BED的面积22.5，则BC=（ ）
A．16B．10C．12D．14
【标准答案】C
【思路指引】
先根据，AB＝6求得DE＝7.5，再根据折叠的性质得到，而，则，得，由此利用勾股定理得到，进而即可求得答案．
【详解详析】
解：四边形是矩形，
，，
∴，
又∵AB＝6，
∴，
解得：DE＝7.5，
将该矩形沿对角线折叠，
，
四边形是矩形，
，
，
，
，
∴在中，，
∴，
故选：C．
【名师指路】
本题考查了折叠的性质：折叠前后的两个图形全等，即对应线段相等，对应角相等．也考查了矩形的性质，等腰三角形的判定与勾股定理的应用，熟练掌握相关图形的性质是解决本题的关键．
10．（2021·江苏丹阳·八年级期中）如图，在正方形中，，点在对角线上任意一点，将正方形绕点逆时针旋转后，点的对应点为，则点到线段距离的最小值为（ ）
A．1B．C．D．2
【标准答案】D
【思路指引】
连接BE、、，由正方形的性质和旋转性质得AE′=CE，BE=BE′，∠∠EBE′=90°，证得△BEE′是等腰直角三角形且∠A′AC=90°，过B作BM⊥于M，则有BM=EE′，只需求出EE′的最小值即可．设AE=x，AE′=CE=，利用勾股定理得出， 从而求出EE′的最小值即可解答．
【详解详析】
解：连接BE、、，
∵∵四边形ABCD是正方形，
∴∠DAC=∠DCA=45°，
由旋转性质得AE′=CE，BE=BE′，∠EBE′=90°，∠D′AA′=∠DCA=45°，
∴△BEE′是等腰直角三角形，∠A′AC=90°，
过B作BM⊥于M，则BM=EE′，
∴求BM的最小值，只需求出EE′的最小值．
设AE=x，AE′=CE=，
在Rt△AEE′中，由勾股定理得：
，
当x=时，2有最小值，最小值为16，
此时，EE′=4，BM=EE′=2，
即点到线段距离的最小值为2，
故选：D．
【名师指路】
本题考查正方形的性质、旋转的性质、等腰直角三角形的性质、勾股定理等知识，熟练掌握相关知识的联系和运算，利用完全平方式的性质是解决问题是解答的关键．
二、填空题
11．（2021·江苏新吴·八年级期末）如图，E为正方形ABCD中BC边上的一点，且AB=3BE=6，M、N分别为边CD、AB上的动点，且始终保持MN⊥AE，则AM+NE的最小值为______．
【标准答案】
【思路指引】
过点E作EF∥MN，过点M作MF∥EN交EF于点F，证得当A、M、F三点在同一直线上时，AM+NE有最小值，即为AF的长，过点M作MG⊥AB于点G，证明Rt△ABE≌Rt△MGN，得到△AEF是等腰直角三角形，再利用勾股定理即可求解．
【详解详析】
解：过点E作EF∥MN，过点M作MF∥EN交EF于点F，连接AF，如图：
则四边形MNEF为平行四边形，
∴MN=EF，MF=NE，MN∥EF，
∴AM+NE=AM+ MFAF，
∴当A、M、F三点在同一直线上时，AM+NE有最小值，即为AF的长，
过点M作MG⊥AB于点G，MN与AE相交于点O，如图：
∵四边形ABCD是正方形，MN⊥AE，
∴∠AON=∠B=90°，AB=BC=MG，
∴∠1+∠3=∠2+∠3=90°，
∴∠1=∠2，
∴Rt△ABE≌Rt△MGN，
∴AE=MN，
∵MN=EF，MN∥EF，
∴AE=MN=EF，AE⊥EF，
∴△AEF是等腰直角三角形，
∵AB=3BE=6，
∴BE=2，
由勾股定理得AE=，
∴AF=，
即AM+NE的最小值为．
故答案为：．
【名师指路】
本题考查了正方形的性质，全等三角形的判定和性质，等腰直角三角形的判定和性质，勾股定理的应用等，正确的确定当A、M、F三点在同一直线上时，AM+NE有最小值，即为AF的长是解题的关键．
12．（2021·江苏·江阴市云亭中学八年级月考）如图，四边形ABCD中，∠A＝90°，AD∥BC，AD