中职数学高教版（2021）基础模块上册第1章 集合1.3 集合的运算获奖教案设计

这是一份中职数学高教版（2021）基础模块上册第1章 集合1.3 集合的运算获奖教案设计，共9页。

1.3 集合的运算
选用教材
高等教育出版社《数学》
（基础模块上册）
授课时长
3课时
授课类型
新授课
教学提示
本课以常见的登记表为载体，通过学生熟悉的情境和问题引入交集，并以此为线索学习并集和补集，借助Venn图，用“数形结合”的方法突破难点；学习进行集合间交、并和补运算．
教学目标
能举例说明什么是两个集合的交集、什么是两个集合的并，什么是一个集合在全集中的补集，并用恰当的符号表示，逐步提升数学抽象等核心素养；经历从两个集合的交集、并集、补集的文字语言描述转化为用数学语言表示的过程，感受数学语言的简洁、严谨；能结合实例理解、区分符号“∩”与“∪”的含义，并能根据需要正确选用，并能求解给定的两个集合之间的交、并、补运算，逐步提升数学运算等核心素养；会借助Venn图分析两个集合之间的交、并、补运算，逐步提升直观想象等核心素养．
教学重点
集合的交集、并集、补集概念的理解．
教学难点
用描述法表示的集合间的交、并、补运算．
教学环节
教学内容
教师
活动
学生
活动
设计
意图
引入
实数之间可以进行运算，如5+2=7,4-3=1, 3×7=21．
类比这些运算，集合之间是否也可以进行运算呢？
提问
思考
引发思考
情境导入
1.3.1 交集
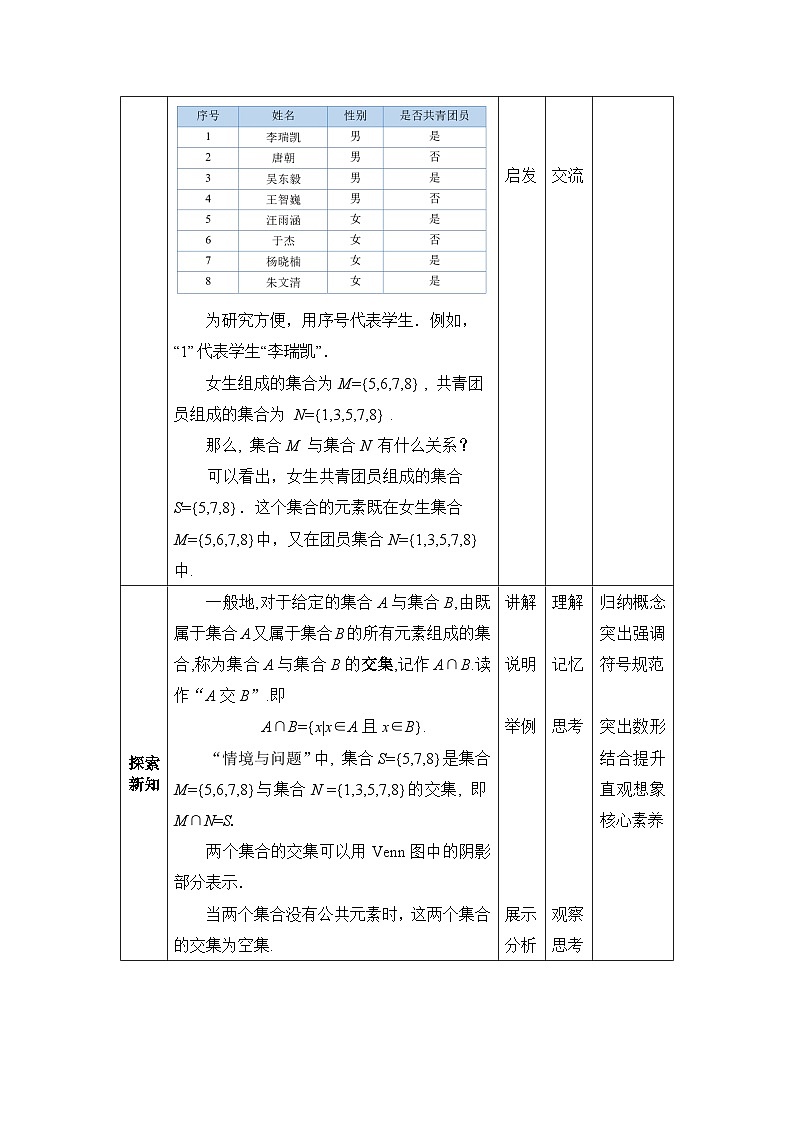
实班第一小组8位学生的登记表：
为研究方便，用序号代表学生．例如，“1”代表学生“李瑞凯”．
女生组成的集合为M={5,6,7,8} , 共青团员组成的集合为 N={1,3,5,7,8} .
那么, 集合M 与集合N 有什么关系？
可以看出，女生共青团员组成的集合S={5,7,8}．这个集合的元素既在女生集合M={5,6,7,8}中，又在团员集合N={1,3,5,7,8}中.
提问
引导
启发
观察
思考
交流
以生活实例创设情境，指导学生观察引发学生思考
探索新知
一般地,对于给定的集合A与集合B,由既属于集合A又属于集合B的所有元素组成的集合,称为集合A与集合B的交集,记作A∩B.读作“A交B”.即
A∩B={x|x∈A且x∈B}.
“情境与问题”中, 集合S={5,7,8}是集合M={5,6,7,8}与集合N ={1,3,5,7,8}的交集, 即M∩N=S.
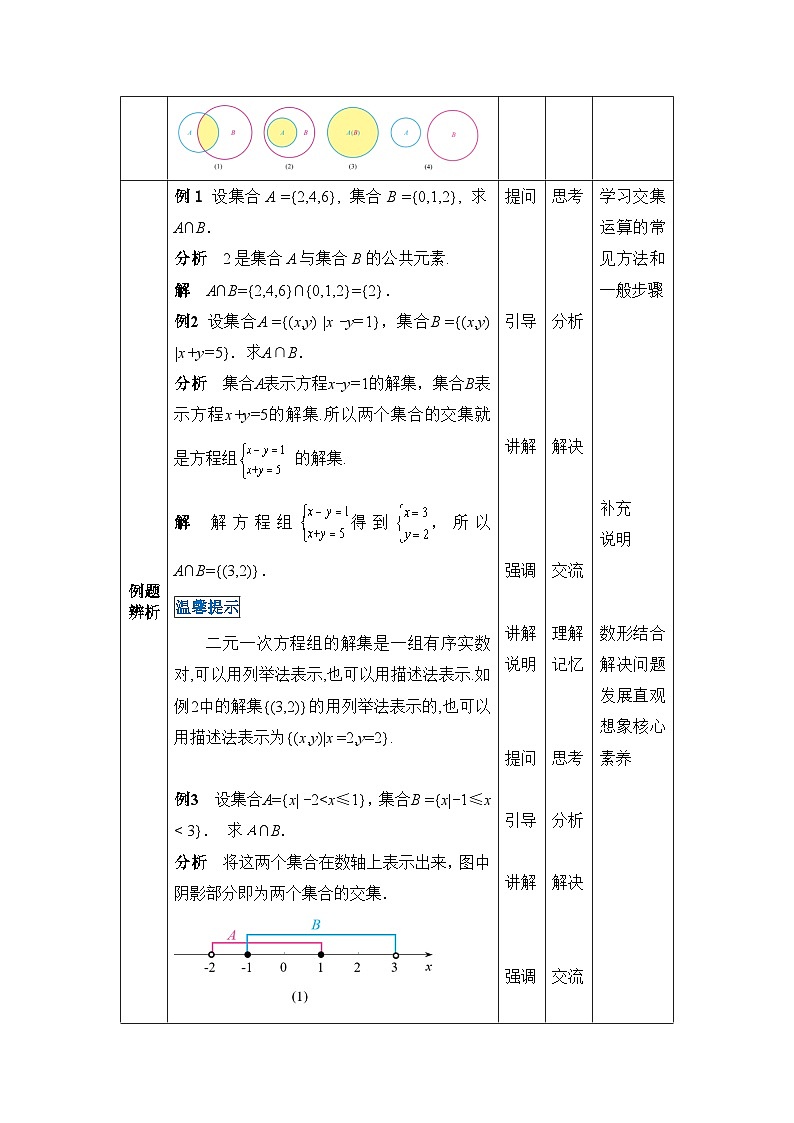
两个集合的交集可以用Venn图中的阴影部分表示．
当两个集合没有公共元素时，这两个集合的交集为空集.
讲解
说明
举例
展示
分析
理解
记忆
思考
观察
思考
归纳概念突出强调符号规范
突出数形结合提升直观想象核心素养
例题辨析
例1 设集合A ={2,4,6}, 集合B ={0,1,2}, 求A∩B．
分析 2是集合A与集合B的公共元素.
解 A∩B={2,4,6}∩{0,1,2}={2}．
例2 设集合A ={(x,y) |x -y=1}，集合B ={(x,y) |x+y=5}．求A∩B．
分析 集合A表示方程x-y=1的解集，集合B表示方程x+y=5的解集.所以两个集合的交集就是方程组 的解集.
解 解方程组得到，所以A∩B={(3,2)}．
温馨提示
二元一次方程组的解集是一组有序实数对,可以用列举法表示,也可以用描述法表示.如例2中的解集{(3,2)}的用列举法表示的,也可以用描述法表示为{(x,y)|x =2,y=2}.
例3 设集合A={x| -2分析 将这两个集合在数轴上表示出来，图中阴影部分即为两个集合的交集．

解 A∩B={x|-2＜x≤1}∩{x|-1≤x＜3}={x|-1≤x≤1}．
提问
引导
讲解
强调
讲解
说明
提问
引导
讲解
强调
思考
分析
解决
交流
理解
记忆
思考
分析
解决
交流
学习交集运算的常见方法和一般步骤
补充
说明
数形结合解决问题发展直观想象核心素养
新知探索
由交集的定义可以推知, 对于任何集合A、B, 有：
(1) A∩B= B∩A ；
(2) A∩A=A ；
(3) A∩=∩A= ；
(4) A∩BA, A∩BB.
结合
图形
进行
说明
分析
思考
领会
举例
总结重要结论加深认识
巩固练习
练习1.3.1
1.设集合A={2,3,4}, 集合B={0,1,2}. 求A∩B．
2.设集合A={(x,y)|x-2y=1}, 集合B={(x,y)|x+2y=3}, 求A∩B．
3.设集合A ={x |x>-1}, 集合A ={x |x≤-2}, 求A∩B．
提问
巡视
指导
思考
动手
求解
交流
及时巩固查漏补缺
情境导入
1.3.2 并集
前面的同学登记表中,设集合T={1,3,5,6,7,8}.集合T表示的是哪些同学组成的集合呢？这个集合的元素与女生组成的集合M={5,6,7,8}和共青团员组成的集合N={1,3,5,7,8}有什么关系呢？
可以看出，集合T的元素是由集合M与集合N的所有元素组成的.
提问
引导
启发
观察
思考
交流
延续实例体现知识的连续性
新知探索
一般地,对于给定的集合A与集合B,由集合A与集合B的所有元素组成的集合称为集合A与集合B的并集,记作A∪B.读作“A并B”.即
A∪B={x|x∈A或x∈B}.
“情境与问题”中, 集合T={1,3,5,6,7,8}是集合M={5,6,7,8}与集合N ={1,3,5,7,8}的并集, 即M∪N=T.
两个集合的并集可以用Veen图中的阴影部分表示．
讲解
说明
举例
展示
分析
理解
记忆
思考
观察
思考
归纳概念强调符号规范
提升直观想象核心素养
例题辨析
例4 设集合A ={1,3,5,7}, 集合B ={0,2,3,4,6}, 求A∪B．
解：
A∪B={1,3,5,7}∪{0,2,3,4,6}={0,1,2,3,4,5,6,7}．
温馨提示
求集合的并集时,相同的元素不能重复出现. 例如，例4中集合A和集合B中都有元素3,但是在A∪B中元素3只出现一次．
例5 设集合A={x|−1分析 将这两个集合在数轴上表示出来，图中阴影部分即为两个集合的并集．
解 A∪B={x |−1提问
引导
讲解
强调
思考
分析
解决
交流
学习并集运算的常见方法和一般步骤
强调数形结合解决问题
新知探索
由并集的定义可以推知, 对于任何集合A、B, 有：
(1) A∪B= B∪A ；
(2) A∪A= A ；
(3) A∪=∪A=A ；
(4) AA∪B, BA∪B.
结合
图形
进行
说明
分析
思考
领会
举例
总结重要结论加深认识
巩固练习
练习1.3.2
1.设集合A={2,3,4}, 集合B={0,1,4}. 求A∪B．
2.设集合A ={x |x≥-1}, 集合A ={x |x≤2}，求A∪B．
3.设集合A={奇数}, 集合B={偶数}. 求A∪B．
4.试给出集合A与集合B, 使A∪B= B.
提问
巡视
指导
思考
动手
求解
交流
及时巩固查漏补缺
情境导入
1.3.3 补集
前面的同学登记表中, 设第一小组所有8名学生组成集合为U={1,2,3,4,5,6,7,8}.那么, 集合U分别与由共青团员组成的集合 {1,3,5,7,8}、由不是共青团员的学生组成的集合E={2,4,6}有什么关系？
显然，集合N与集合E都是集合U的子集，那么，这两个子集即集合N与集合E又有什么关系呢？.
提问
引导
启发
观察
思考
交流
延续实例体现知识的连续性
新知探索
研究某些集合时,如果这些集合是一个给定集合的子集，那么这个给定的集合称为全集,通常用字母U表示.在研究数集时，通常把实数集R作为全集．
“情境与问题”中, 第一小组8名同学组成的集合U={1,2,3,4,5,6,7,8}就是这个问题中给定的全集.
前面的同学登记表中,不是共青团员的学生组成的集合是E={2,4,6}.集合E的元素都属于全集U但不属于共青团员组成的集合N ={1,3,5,7,8}.
一般地，如果集合A是全集U的一个子集，则由集合U中不属于集合A的所有元素组成的集合称为集合A在全集U中的补集，记作∁UA．即
∁UA={x|x∈U且xA}.
“情境与问题”中,不是共青团员的学生组成的集合 E={2,4,6}就是共青团员组成的集合N={1,3,5,7,8}在全集U={1,2,3,4,5,6,7,8}中的补集，即∁UN= E．
集合A在全集U中的补集可以用Veen图中的阴影部分表示．
讲解
说明
举例
展示分析
理解
记忆
思考
观察
思考
归纳概念突出强调符号规范以及知识之间的联系
数形结合
提升直观想象核心素养
例题辨析
例6 设全集U={x∈N|x＜7}，集合A={1,2,4,6},求∁UA．
解 因为全集U={x∈N|x＜7}={0,1,2,3,4,5,6}，所以集合A={1,2,4,6}的补集为
∁UA={0,3,5}.
例7 设全集U= R，集合A={x|−2≤x＜1}．求∁A．
分析 将集合A在数轴上表示出来, 图中阴影部分即为集合A的补集．
解 ∁UA={x|x＜−2或x≥1}.
温馨提示
用数轴求补集的时候要特别注意端点的取舍.
提问
引导
讲解
强调
说明
思考
分析
解决
交流
注意
示范补集运算的常见方法
强调数形结合解决问题
补充
新知探索
由补集的定义可以推知, 对于任何集合A, 有：
(1) A∩∁UA= ；
(2) A∪∁UA =U ；
(3)∁U(∁UA)=A.
结合
图形
进行
说明
分析
思考
领会
举例
总结结论加深认识
巩固练习
练习1.3.3
1. 设全集U={x∈N|x＜5}, 集合A={0}, 求∁UA．
2. 设全集U=R, 集合A={x|x＞1} , 求UA
3. 设全集U=R, 求∁U Q．
4. 已知全集U={三角形}, 集合A={直角三角形},求
∁UA．
提问
巡视
指导
思考
动手
求解
交流
及时巩固查漏补缺
归纳总结
引导
提问
回忆
反思
培养学生
总结学习
过程能力
布置作业
1.书面作业：完成课后习题和学习与训练；
2.查漏补缺：根据个人情况对课题学习复习与回顾;
3.拓展作业：阅读教材扩展延伸内容.
说明
记录
继续探究
延伸学习