2024年浙江省宁波市南三县中考诊断性考试 数学试题及答案

这是一份2024年浙江省宁波市南三县中考诊断性考试 数学试题及答案，文件包含答案数学答案docx、2024年南三县诊断性考试数学卷pdf等2份试卷配套教学资源，其中试卷共12页， 欢迎下载使用。

一、选择题（每题3分，共30分）
二、填空题（每题4分，共24分）
三、解答题（共66分）
17.（本题6分）
=1+3-7………………2分
=-3………………3分
=x2-1+2x-2x2………………5分
=-x2+2x-1………………6分
18.（本题6分）
（1）画图正确(画法不唯一) --------------------3分

（2）画图正确 (画法不唯一) --------------------6分
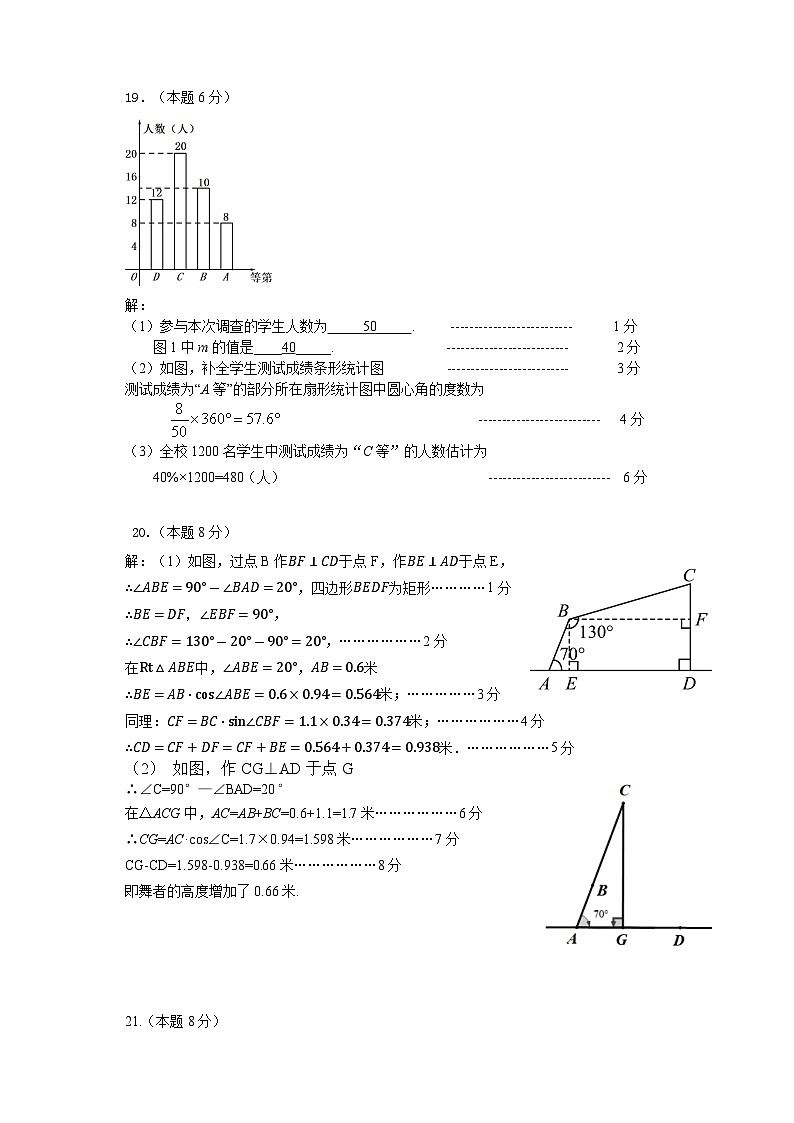
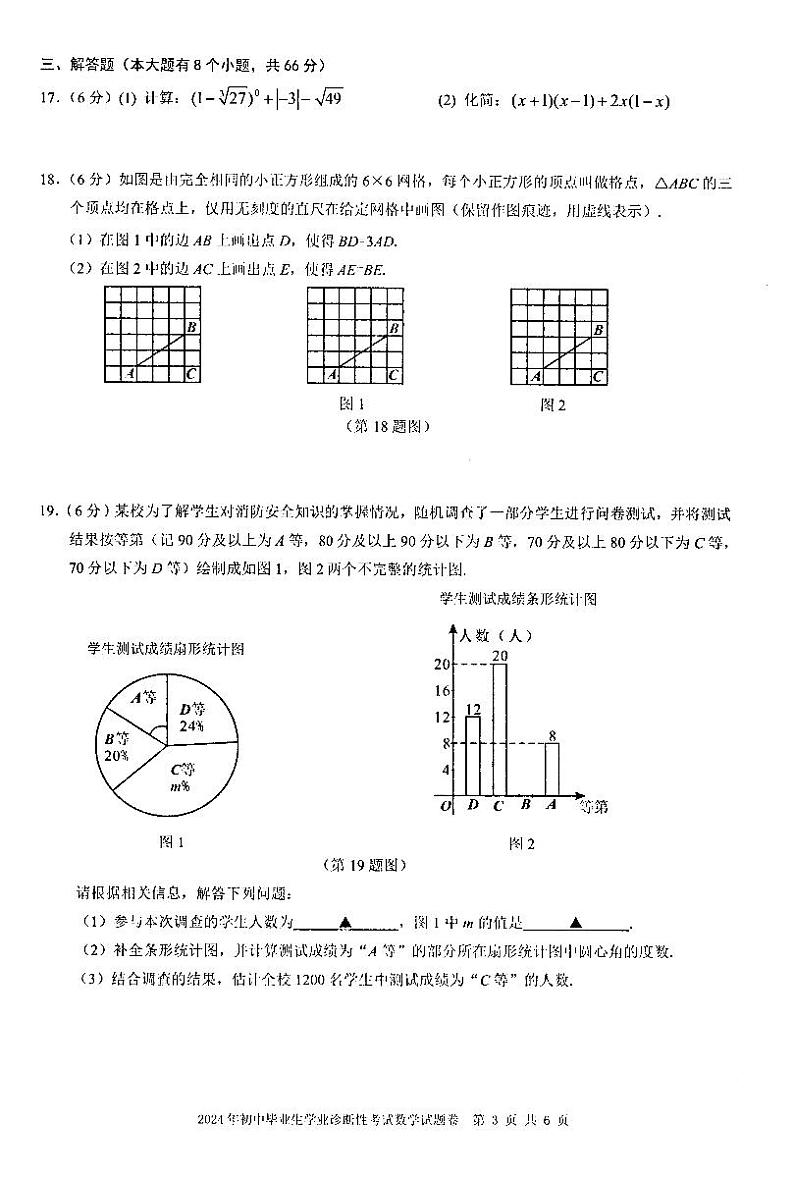
19．（本题6分）
解：
（1）参与本次调查的学生人数为_____50_____. -------------------------- 1分
图1中m的值是____40_____. -------------------------- 2分
如图，补全学生测试成绩条形统计图 -------------------------- 3分
测试成绩为“A等”的部分所在扇形统计图中圆心角的度数为
-------------------------- 4分
全校1200名学生中测试成绩为“C等”的人数估计为
40%×1200=480（人） -------------------------- 6分
20.（本题8分）
解：（1）如图，过点B作BF⊥CD于点F，作BE⊥AD于点E，
∴∠ABE=90°-∠BAD=20°，四边形BEDF为矩形…………1分
∴BE=DF，∠EBF=90°，
∴∠CBF=130°-20°-90°=20°，………………2分
在Rt△ABE中，∠ABE=20°，AB=0.6米
∴BE=AB⋅cs∠ABE=0.6×0.94=0.564米；……………3分
同理：CF=BC⋅sin∠CBF=1.1×0.34=0.374米；………………4分
∴CD=CF+DF=CF+BE=0.564+0.374=0.938米．………………5分
（2） 如图，作CG⊥AD于点G
∴∠C=90°—∠BAD=20°
在△ACG中，AC=AB+BC=0.6+1.1=1.7米………………6分
∴CG=AC·cs∠C=1.7×0.94=1.598米………………7分
CG-CD=1.598-0.938=0.66米………………8分
即舞者的高度增加了0.66米.
21.（本题8分）
解：（1）由图象可知，甲乙两地的距离为480km
在0-3小时快车和慢车一起行驶了3小时，3-4小时快车出现故障停止前行、仅有慢车行驶
则慢车速度为=60km/h
设快车速度为v，则有：（v+60）×3=480，解得v=100km/h …………2分
∵慢车行驶时间为h，
∴C点的横坐标为8
∴C点的坐标为（8,480）； …………4分
在快车出现故障前，两车相距200km 所用时间为：
（480-200）÷（100+60）=74h；
（或设慢车时间为t，则60t+100t+200=480，解得t=74）…………6分
在快车出现故障后，慢车1小时行驶了60km，然后两车共同行驶了200-60=140km
共同行驶时间为140÷（100+60）=78h
∴两车相距200km 所用时间为4+78=398h．
（或60t+100（t-1）-480=200，解得t=398）…………8分
答：两车相距200km 所用时间为和．
（本题10分）
（1）证明：∵平分，∴，…………1分
∵四边形是平行四边形，∴且，
∴，∴，∴，…………2分
∵AF⊥BE，∴， …………3分
∵，∴△AFE≌△GFB（ASA），
∴， …………4分
∵，∴四边形AEGB是平行四边形，
∵，∴四边形是菱形； …………5分
（2）解：∵，∴，…………6分
过点F作于点M，如图所示：
∵AG⊥BE，
，
∴，∴， …………8分
∴，∴，∴，
在中，根据勾股定理得：． …………10分
23.（本题10分）
（1）如图，以O为原点，建立如图所示的坐标系，
∴A（0，1），C（6，3.4），∴设抛物线解析式为y＝ax2+bx+1，……1分
∵OF＝DF＝BD＝2，DE＝BC，∴抛物线的对称轴为直线 QUOTE ，
∴y＝ax2﹣10ax+1，将C（6，3.4）代入解析式得， QUOTE ，
∴ QUOTE ． …………3分
（2）如图，建立与（1）相同的坐标系，
∵CC'＝1.2，∴C'为（6，4.6），
∵改造后对称轴不变，设改造后抛物线解析式为y＝ax2﹣10ax+1，
将C'（6，4.6）代入解析式得 QUOTE ， …………4分
∴ QUOTE ，
∴G为 QUOTE ，G'为 QUOTE ，∴ QUOTE ， …………5分
∴共需改造经费 QUOTE ，∴能完成改造． …………6分
（3）如图，设改造后抛物线解析式为y＝ax2﹣10ax+1，
则G'为（2，﹣16a+1），E'为（4，﹣24a+1），…………7分
∴ QUOTE ，……8分
由题意可列不等式，（﹣40a﹣4）×200×60≤32000，解得 QUOTE ，……9分
∵CC'＝EE'＝﹣24a+1﹣3.4，∴ QUOTE 时，CC'的值最大，为1.6米． …………10分
24.（12分）
（1）解：①平行四边形是倍分四边形（√ ）…………1分
②梯形是倍分四边形（×） …………2分
（2）解：∵倍分四边形ABCD中，AC是倍分线，
∴S△ABC=S△ADC. …………3分
如图所示，过点D作DE⊥AC于点E，
∵AC⊥AB，AB=3，AD=DC=5，
∴AB=DE=3，AE=EC. …………4分
在Rt△AED中，AE=AD2-DE2=4，
∴AC=2AE=8，在Rt△ACB中，BC=AC2+AB2=32+82=73. …………5分
（3）①如图所示，连接NC，BM，OM， 设OM,CN交于点G，
∵BC为⊙O直径，∴∠BMC=∠BNC=90°，
∵BA=BC，∴AM=AC，即M是AC的中点，
∴MO=12AB，MO∥AB
∵四边形BCMN是倍分四边形．
若BM是倍分线，则点N,C到BM的距离相等，
而BM是∠ABC的角平分线，点C,A到BM的距离相等，点N,A不重合，故BM不是倍分线，
∴NC是倍分线，∴NB=MG， …………6分
又∵MO∥AB，∴△CGO∽△CNB，
∴OGNB=COCB=12，∴OG=12NB，
设BN=a，则MO=MG+OG=a+12a=32a，
∴AB=2MO=3a，又∵BA=BC，∴BC=3a，AN=2a.
在Rt△BCN中，CN=BC2-BN2=3a2-a2=22a，
在Rt△ANC中，AC=CN2+AN2=22a2+2a2=23a
∴AM=12AC=3a，BM=AB2-AM2=3a2-3a2=6a.
∴sin∠ACB=BMBC=6a3a=63…………8分
②如图所示，设OM,NC交于点G，连接BG，过点F作FH⊥CG交NC于点H，
由①可得MG∥NB,MG=BN，则四边形BNMG是平行四边形，
∵点F是OC的中点，OF=3
∴OC=6，则BC=12=AB，
∵BC=3BN，
∴NB=4，则AN=AB-BN=12-4=8
∴NC=BC2-BN2=122-42=82，
∵NG=12NC=42，
∴DG=12NG=22， …………10分
∵FH⊥NC,GO⊥NC，
∴GO∥FH，∴△CHF∽△CGO
∴HFGO=CFCO=12，∴GH=12GC=14NC=22，FH=12GO=14NB=1
∵HF∥GM，∴△EHF∽△EGM，
∴HFGM=EHEG，即14=EHEG
∴GE=45GH=825
∴DE=DG+GE=22+825=1852．…………12分
1
2
3
4
5
6
7
8
9
10
D
C
B
B
B
A
D
C
B
A
11
12
13
14
15
16
m≥3
52或10